Câu 3 phần c giúp mình với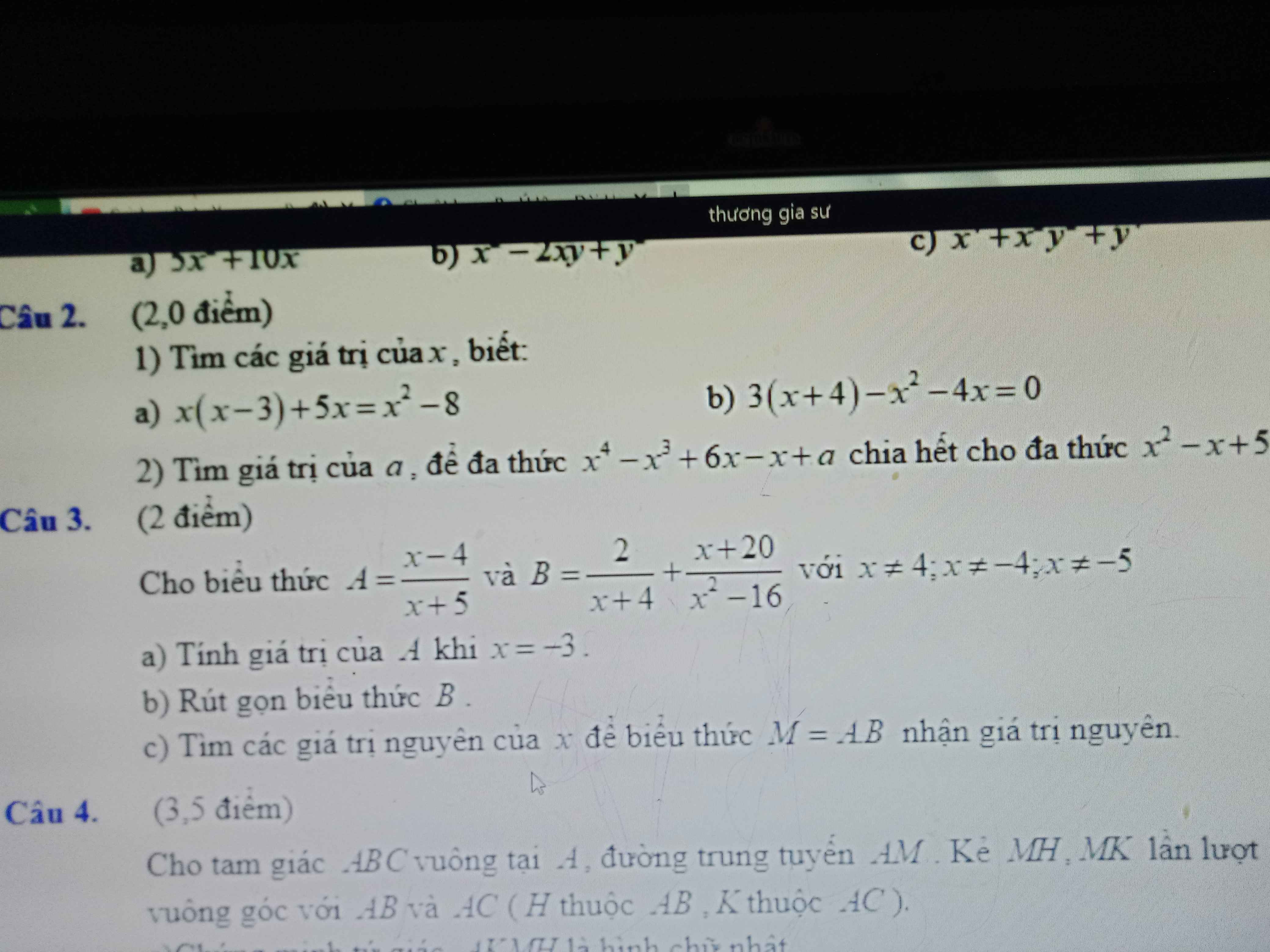

Những câu hỏi liên quan
Giúp mình câu 2 phần 2 và câu 3 phần 2 với

câu 2 phần 2:
\(\left\{{}\begin{matrix}4x+3y=11\\4x-y=7\end{matrix}\right.\)\(< =>\left\{{}\begin{matrix}4y=4\\4x-y=7\end{matrix}\right.< =>\left\{{}\begin{matrix}y=1\\x=2\end{matrix}\right.\).Vậy hệ pt có nghiệm
(x,y)=(2;1)
caau3 phần 2:
\(x^2-2x+m-1=0\)(1)
\(\Delta'=\left(-1\right)^2-\left(m-1\right)=1-m+1=2-m\)
để pt (1) có 2 nghiệm x1,x2<=>\(\Delta'\ge0< =>2-m\ge0< =>m\le2\)
theo vi ét=>\(\left\{{}\begin{matrix}x1+x2=2\left(1\right)\\x1.x2=m-1\left(3\right)\end{matrix}\right.\)
có: \(x1^4\)\(-x1^3=x2^4-x2^3\)
\(< =>x1^4-x2^4-x1^3+x2^3=0\)
\(< =>\left(x1^2-x2^2\right)\left(x1^2+x2^2\right)-\left(x1^3-x2^3\right)\)\(=0\)
\(< =>\left(x1-x2\right)\left(x1+x2\right)\left[\left(x1+x2\right)^2-2x1x2\right]\)\(-\left(x1-x2\right)\left(x1^2+x1x2+x^2\right)=0\)
\(< =>\)\(\left(x1-x2\right)\left[2.2^2-2\left(m-1\right)-\left(x1^2+x1x2+x2^2\right)\right]=0\)
\(< =>.\left(x1-x2\right)\left[8-2m+2-\left(x1+x2\right)^2+x1x2\right]=0\)
<=>\(\left(x1-x2\right)\left[10-2m-4+m-1\right]=0\)
\(< =>\left(x1-x2\right)\left(5-m\right)=0\)
\(=>\left[{}\begin{matrix}x1-x2=0\\5-m=0\end{matrix}\right.< =>\left[{}\begin{matrix}x1=x2\left(2\right)\\m=5\left(loai\right)\end{matrix}\right.\)
thế(2) vào(1)=>\(x1=x2=1\left(4\right)\)
thế (4) vào (3)=>\(m-1=1=>m=2\left(TM\right)\)
vậy m=2 thì....
Đúng 0
Bình luận (0)
A = 1+ 1 phần 2+ 1 phần 3+...+1 phần 255<8
giúp mình với mình cần gấp
giúp câu trả lời cho nguyễn thu ánh!!![]()
mọi người giúp mình với, mẹ mình đang mắng mình giúp mình
Câu 1 với câu 3 phần 1 mình giải đc rồi nhưng còn câu còn lại và câu 3 phần 2 chưa giải được mong các bạn, anh chị giúp mình nhé

Bài 4:
b: Xét ΔAHB vuông tại H có HM là đường cao
nên \(AM\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HN là đường cao
nên \(AN\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AM\cdot AB=AN\cdot AC\)
Đúng 0
Bình luận (0)
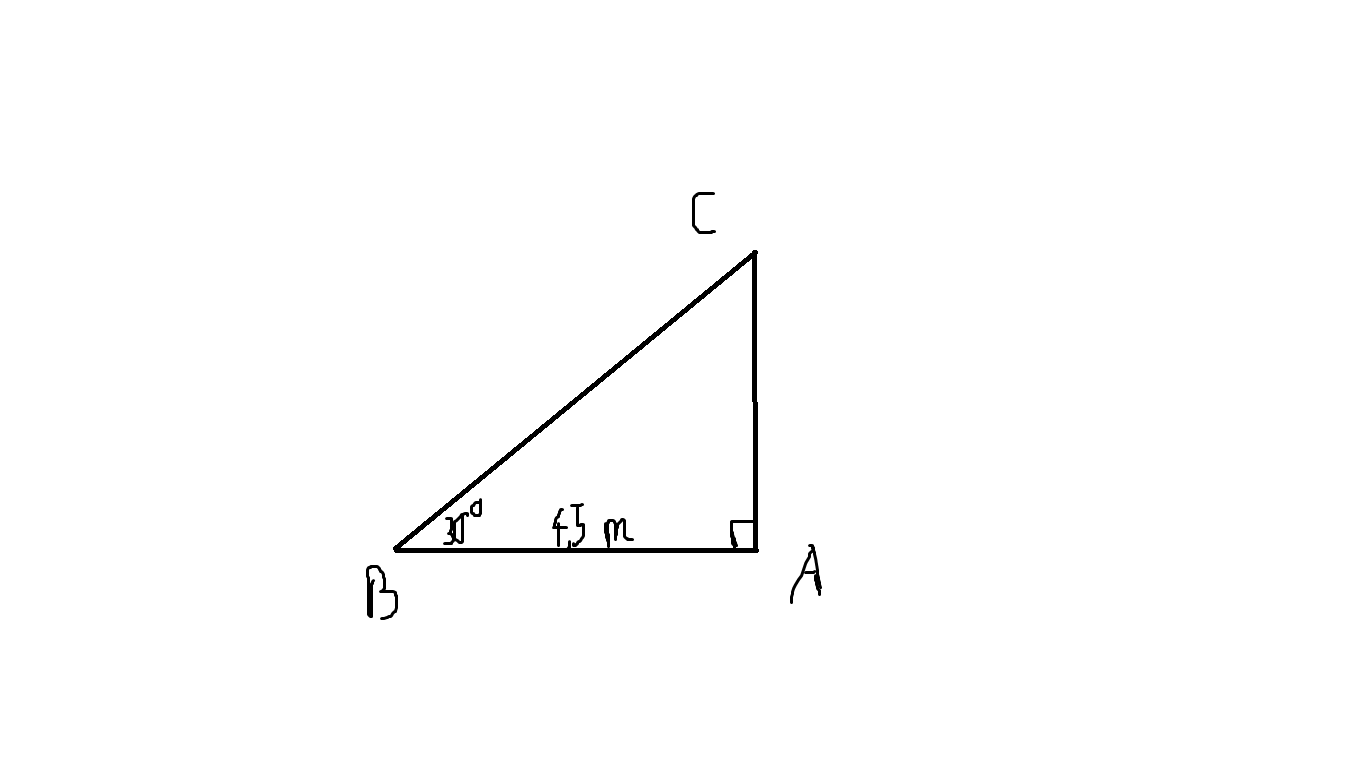
\(TanB=\dfrac{AC}{AB}\Rightarrow Tan30^o=\dfrac{AC}{4,5}\Rightarrow AC=Tan30^o.4,5=\dfrac{3\sqrt{3}}{2}\left(m\right)\)
\(CosB=\dfrac{AB}{BC}\Rightarrow Cos30^o=\dfrac{4,5}{BC}\Rightarrow BC=Cos30^o.4,5=\dfrac{9\sqrt{3}}{4}\)
Chiều cao ban đầu của cây tre là: \(\dfrac{3\sqrt{3}}{2}+\dfrac{9\sqrt{3}}{4}=\dfrac{15\sqrt{3}}{4}\approx6,5\left(m\right)\)
Đúng 0
Bình luận (0)
Giúp mình phần câu b,c với ạ mình cần gấp 



Giúp mình với, câu 3 phần II
Giúp mình phần 2 câu 3 với
Gọi a (km/h) và b (km/h) lần lượt là vận tốc của người thứ nhất và vận tốc của người thứ hai. ĐK: b>a>0.
Quãng đường người thứ nhất đi được trong 1h30'=1,5h là 1,5a km.
Quãng đường người thứ hai đi được trong 1h15'=1,25h là 1,25b km.
Ta có: 1,5a+1,25b=90 (1).
Vận tốc của người thứ hai hơn vận tốc người thứ nhất 6 km/h, ta có b-a=6 (2).
Giải hệ phương trình gồm (1) và (2), ta suy ra a=30 (nhận) và b=36 (nhận).
Vậy vận tốc của người thứ nhất là 30 km/h, vận tốc của người thứ hai là 36 km/h.
Đúng 1
Bình luận (0)
Ai giúp mình câu 3 phần 1 với ạ mình cần gấp
Giúp mình câu 3 phần c, hết câu 4 ạ

Câu 4:
a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow AC^2=15^2-9^2=144\)
hay AC=12(cm)
Xét ΔABC có AB<AC<BC(9cm<12cm<15cm)
nên \(\widehat{ACB}< \widehat{ABC}< \widehat{BAC}\)(Định lí quan hệ giữa cạnh và góc đối diện trong tam giác)
b) Xét ΔABC vuông tại A và ΔAEC vuông tại A có
AB=AE(gt)
AC chung
Do đó: ΔABC=ΔAEC(Hai cạnh góc vuông)
Đúng 2
Bình luận (0)
c) Xét ΔCEB có
CA là đường trung tuyến ứng với cạnh BE(gt)
BH là đường trung tuyến ứng với cạnh CE(gt)
CA cắt BH tại M(gt)
Do đó: M là trọng tâm của ΔCBE(Tính chất ba đường trung tuyến của tam giác)
Suy ra: \(CM=\dfrac{2}{3}CA\)
hay \(CM=\dfrac{2}{3}\cdot12=8\left(cm\right)\)
d) Xét ΔCEB có
A là trung điểm của BE(gt)
AK//CE(gt)
Do đó: K là trung điểm của BC(Định lí 1 đường trung bình của tam giác)
Xét ΔCBE có
M là trọng tâm của ΔCBE(cmt)
EK là đường trung tuyến ứng với cạnh BC(cmt)
Do đó: E,M,K thẳng hàng(đpcm)
Đúng 2
Bình luận (0)





![𒅒[̲̅t̲̅]â[̲̅y̲̅]♜[̲̅d̲̅]...](https://hoc24.vn/images/avt/avt6104997_256by256.jpg)



















