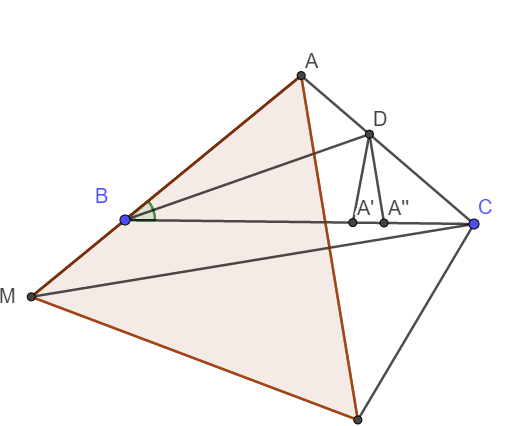
a) Trên BC lấy điểm A' và A'' sao cho BA' = BA;  BA'' = BD

Do BD là phân giác góc ABA' nên ta có ngay \(\Delta ABD=\Delta A'BD\left(c-g-c\right)\) 

\(\Rightarrow AD=A'D\) ; \(\widehat{BA'D}=\widehat{BAD}=180^o-40^o.2=100^o\)

\(\Rightarrow\widehat{DA'A''}=80^o\)

Xét tam giác cân BDA'' có: \(\widehat{DBA''}=20^o\Rightarrow\widehat{BA''D}=\frac{180^o-20^o}{2}=80^o\)

Suy ra DA' = DA'' và \(\widehat{A''DC}=\widehat{DA''A'}-\widehat{ACB}=40^o\)

Nên DA'' = CA''

Tóm lại thì AD = DA' = DA'' = A''C nên BC = BA''+ A''C = BD + AD

b)  Vẽ tam giác đều AMF. 

Ta có ngay \(\widehat{MAF}=60^o\Rightarrow\widehat{CAF}=100^o-60^o=40^o\)

Suy ra \(\Delta ABC=\Delta CAF\left(c-g-c\right)\)

\(\Rightarrow AC=CF\)

Từ đó ta có \(\Delta AMC=\Delta FMC\left(c-c-c\right)\)

\(\Rightarrow\widehat{AMC}=\widehat{FMC}\) hay MA là phân giác óc AMF.

Vậy nên \(\widehat{MAC}=30^o\)

Làm ơn giúp mk với ạ cảm ơn các bạn nhiều

Đề sai trầm trọng luôn

∆ABC có:

∠A + ∠ABC + ∠C = 180⁰ (tổng ba góc trong ∆ABC)

⇒ ∠A = 180⁰ - ∠C - ∠ABC

= 180⁰ - 40⁰ - 80⁰

= 60⁰

Do BD là tia phân giác của ∠ABC

⇒ ∠ABD = ∠ABC : 2 = 80⁰ : 2 = 40⁰

∆ABD có:

∠A + ∠ABD + ∠ADB = 180⁰ (tổng ba góc trong ∆ABD)

⇒ ∠ADB = 180⁰ - ∠A - ∠ABD

= 180⁰ - 60⁰ - 40⁰

= 80⁰

Ta có:

∠ADB + ∠BDC = 180⁰ (kề bù)

⇒ ∠BDC = 180⁰ - ∠ADB

= 180⁰ - 80⁰

= 100⁰

a) Xét tam giác ABC vuông tại A có:
* \(BC^2=AB^2+AC^2\)(định lý Py-ta-go)
\(< =>10^2=6^2+AC^2\)
\(< =>AC^2=100-36\)
\(< =>AC=\sqrt{64}\)
\(< =>AC=8\)

Chu vi tam giác ABC là : \(AB+AC+BC=6+10+8=24\left(cm\right)\)

Diện tích tam giác ABC là: \(\frac{AB.AC}{2}=\frac{6.8}{2}=24\left(cm^2\right)\)

b) Ta có: BD là phân giác của góc B (gt)
=> \(\frac{DA}{DC}=\frac{BA}{BC}\)(tính chất đường phân giác trong 1 tam giác)
Mà \(\frac{BA}{BC}=\frac{6}{10}=\frac{3}{5}\)
=>\(\frac{DA}{DC}=\frac{3}{5}\)

c) Xét tam giác ABI có:
* BD là phân giác góc B (gt)
* BD là đường cao (AI vuông góc BD)
=> Tam gi1c ABI cân tại B
=> BA = BI (tính chất)

Xét tam giác ABD và tam giác IBD có:
*AB = IB (cmt)
*Góc ABD = Góc IBD (BD là phân giác)
*BD là cạnh chung
=> tam giác ABD = tam giác IBD (c-g-c)
=> Góc BAD = Góc BID (tính chất) 
Mà góc BAD = 90 độ (tam giác ABC vuông tại A)
=> Góc BID = 90 độ 

17 đó

k nha

chúc bạn học giỏi

17 nha

17 nha 

k cho mik nha >.<!!

A) Xét tam giác ABD và tam giác EBD có 

  BD ( cạnh chung )

\(\widehat{CBD}\)= \(\widehat{ABD}\)( giả thiết )

 \(\Rightarrow\)tam giác ABD = tam giác EBD ( cạnh huyền - góc nhọn )

 \(\Rightarrow\)DA=DE (  hai cạnh tương ứng )

  b) mà theo phần a ta lại có : \(\widehat{EDB}\)=\(\widehat{EDB}\)( hai góc tương ứng ) 

       mà \(\widehat{ADF}\)=\(\widehat{EDC}\)( hai góc đối đỉnh )

  \(\Rightarrow\)\(\widehat{CDB}\)=\(\widehat{FDB}\)( Theo hai cm trên )

        BD ( cạnh chung )

  \(\widehat{EBD}\)=\(\widehat{ABD}\)( giả thiết )

  vậy suy ra tam giác BDF = tam giác BDC ( G-C-G)

 C) Theo phần  a ta có AD =ED

                       B ta lại có :FD = DC 

      suy ra tứ giác AECF là hình thang cân 

  suy ra AE song song FC

chăm trả lời câu hỏi nhề 

a: Xét ΔBAD và ΔBED có

BA=BE

góc ABD=góc EBD

BD chung

=>ΔBAD=ΔBED

=>DA=DE

b: BA=BE

DA=DE
=>BD là trung trực của AE

=>BD vuông góc AE

c: góc EDC+góc C=90 độ

góc ABC+góc C=90 độ

=>góc EDC=góc ABC

ke hinh di ban