Cho đường tròn \(\left(O\right)\) và điểm \(A\) bên ngoài đường tròn, từ \(A\) vẽ tiếp tuyến \(AB\) với đường tròn (\(B\) là tiếp điểm). Kẻ đường kính \(BC\) của đường tròn \(\left(O\right)\). \(AC\) cắt đường tròn \(\left(O\right)\) tại \(D\) (\(D\) khác \(C\)).
\(a\)) Chứng minh \(BD\) vuông góc \(AC\) và \(AB^2=AD\cdot AC\).
\(b\)) Từ \(C\) vẽ dây \(CE//OA,BE\) cắt \(OA\) tại \(H\). Chứng minh \(H\) là trung điểm \(BE\) và \(AE\) là tiếp tuyến của đường tròn \(\left(O\right)\).
\(c\)) Tia \(OA\) cắt đường tròn \(\left(O\right)\) tại \(F\). Chứng minh \(FA\cdot CH=HF\cdot CA\).
Cho đường tròn left(Oright) và điểm A bên ngoài đường tròn, từ A vẽ tiếp tuyến AB với đường tròn (B là tiếp điểm). Kẻ đường kính BC của đường tròn left(Oright). AC cắt đường tròn left(Oright) tại D (D khác C).
a) Chứng minh BD vuông góc AC và AB^2ADcdot AC.
b) Từ C vẽ dây CE//OA,BE cắt OA tại H. Chứng minh H là trung điểm BE và AE là tiếp tuyến của đường tròn left(Oright).
c) Tia OA cắt đường tròn left(Oright) tại F. Chứng minh FAcdot CHHFcdot CA.
Đọc tiếp
Cho đường tròn left(Oright) và điểm A nằm ngoài đường tròn với OA2R.Từ A vẽ hai tiếp diễn AB,AC của đường tròn left(Oright) (B,C là tiếp điểm).Vẽ dây BE của đường tròn (O) song song với AC;AE cắt đường tròn tại D (D khác E );BD cắt AC tại S.Gọi M là trung điểm của đoạn thẳng DE . a) Chứng minh năm điêm A,B,C,O,M cùng thuộc một đường tròn b) Chứng minh SC2SB.SD và SASC c)Hai đường thẳng DE và BC cắt nhau tại V ; đường thẳng SV cắt BE tại H .Chứng minh ba điểm H,C,O thẳng hàng .
Đọc tiếp
Cho đường tròn \(\left(O\right)\) và điểm A nằm ngoài đường tròn với \(OA>2R\).Từ A vẽ hai tiếp diễn \(AB,AC\) của đường tròn \(\left(O\right)\) (B,C là tiếp điểm).Vẽ dây BE của đường tròn (O) song song với AC;AE cắt đường tròn tại D (D khác E );BD cắt AC tại S.Gọi M là trung điểm của đoạn thẳng DE .
a) Chứng minh năm điêm A,B,C,O,M cùng thuộc một đường tròn
b) Chứng minh SC2=SB.SD và SA=SC
c)Hai đường thẳng DE và BC cắt nhau tại V ; đường thẳng SV cắt BE tại H .Chứng minh ba điểm H,C,O thẳng hàng .
a: ΔODE cân tại O
mà OM là trung tuyến
nên OM vuông góc DE
=>góc OMA=90 độ=góc OCA=góc OBA
=>O,A,B,M,C cùng thuộc 1 đường tròn
b: Xét ΔBSC và ΔCSD có
góc SBC=góc SCD
góc S chung
=>ΔBSC đồng dạng với ΔCSD
=>SB/CS=SC/SD
=>CS^2=SB*SD
góc DAS=gócEBD
=>góc DAS=góc ABD
=>ΔSAD đồng dạng với ΔSBA
=>SA/SB=SD/SA
=>SA^2=SB*SD=SC^2
=>SA=SC
c; BE//AC
=>EH/SA=BH/SC=HJ/JS
mà SA=SC
nênHB=EH
=>H,O,C thẳng hàng
Đúng 0
Bình luận (0)
Trong mặt phẳng Oxy, cho đường tròn \(\left(C\right):\left(x-1\right)^2+\left(y-2\right)^2=9\). Viết phương trình đường tròn ảnh của đường tròn đã cho qua phép quay \(Q_{\left(O,-90^0\right)}\) với O là gốc tọa độ ?
Cho đường tròn left(O_1right) tiếp xúc trong với đường tròn $(O)$ tại $A$. Đường kính $AB$ của đường tròn $(O)$ cắt đường tròn left(O_1right) tại điểm thứ hai $C$ khác $A$. Từ $B$ vẽ tiếp tuyến $BP$ với đường tròn left(O_1right) cắt đường tròn left(Oright) tại $Q$. Chứng minh $AP$ là tia phân giác của góc widehat{QAB}.
Đọc tiếp
Cho đường tròn \(\left(O_1\right)\) tiếp xúc trong với đường tròn $(O)$ tại $A$. Đường kính $AB$ của đường tròn $(O)$ cắt đường tròn \(\left(O_1\right)\) tại điểm thứ hai $C$ khác $A$. Từ $B$ vẽ tiếp tuyến $BP$ với đường tròn \(\left(O_1\right)\) cắt đường tròn \(\left(O\right)\) tại $Q$. Chứng minh $AP$ là tia phân giác của góc \(\widehat{QAB}\).
có góc AQB= 90 độ( góc nội tiếp chắn nửa đường tròn tâm O) Hay góc AQP=90 độ => góc QAP= 90 độ- góc QPA=90 độ-1/2sđ cung AP
có góc APC= 90 độ( góc nội tiếp chắn nửa đường tròn tâm O1)=> góc PAC=90 độ - góc PCA=90 độ - 1/2sđ cung AP
Vì vậy góc QAP= góc PAC hay AP là tia phân giác của góc QAB
Ta có: góc BQA =90o (góc nội tiếp chắn nửa (O))
Xét Δ PQA vuông tại Q có: góc QAP + góc QPA =90o ⇒ góc QAP=90o- góc QPA
Mà góc QPA =1/2 sđ cung PA ( góc QPA là góc tạo bởi tia tiếp tuyến cà dây cung chắn cung AP của (O1))
⇒góc QAP=90o- 1/2 sđ cung PA (1)
Xét ΔCPA vuông tại P ( vì góc CPA là góc nội tiếp chắn nửa (O1)) có
góc PCA + góc PAC =90o⇒góc PAC =90o-góc PCA
mà góc PCA =1/2 sđ cung PA ( góc nội tiếp chắn cung PA )
⇒góc PAC= 90o-1/2 sđ cung PA (2)
Từ (1) và (2) ⇒ góc QAP=góc PAC ⇒ AP là tia phân giác của góc QAB
Vì góc AQP là có nội tiếp chắn nửa đường tròn của (O)
=> góc AQP= 90 độ
xét Δ AQP vuông tại Q có:
góc QAP+ góc QPA= 90 độ
Vì góc CPA là góc nội tiếp chắn nửa đường tròn của (O1)
=> góc CPA= 90 độ
Ta có: góc BPC+ góc CPA+ góc APQ= 180 độ
=> góc BPC + 90 độ+ góc APQ= 180 độ
=> góc BPC+ góc APQ= 90 độ
=> góc QAP= góc BPC( cùng phụ với góc APQ)
Lại có: góc BPC là góc tạo bởi tia tiếp tuyến và dây cung chắn cung PC của (O1)
góc PAC là góc nội tiếp chắn cung PC của (O1)
=> góc BPC= góc PAC
=> góc QAP= góc PAC( cùng = góc BPC)
=> AP là tia phân giác của góc QAB( đpcm)
Xem thêm câu trả lời
Cho đường tròn \(\left(O\right)\) và hai điểm \(A,B\). Một điểm \(M\) thay đổi trên đường tròn \(\left(O\right)\) . Tìm quỹ tích điểm \(M'\) sao cho \(\overrightarrow{MM'}+\overrightarrow{MA}=\overrightarrow{MB}\)
Cho đường tròn left(Oright) và điểm M nằm ngoài đường tròn. Từ M, vẽ các tiếp tuyến MA,MB (A,B là các tiếp điểm). Lấy I nằm trong cung nhỏ AB (I khác A,B). Từ I, vẽ tiếp tuyến thứ ba của đường tròn left(Oright), tiếp tuyến đó cắt MA,MB tại E,F. Cho hat{AOB}120^o, tìm giá trị nhỏ nhất của S_{OEF}.
Đọc tiếp
Cho đường tròn \(\left(O\right)\) và điểm \(M\) nằm ngoài đường tròn. Từ \(M\), vẽ các tiếp tuyến \(MA,MB\) (\(A,B\) là các tiếp điểm). Lấy \(I\) nằm trong cung nhỏ \(AB\) (\(I\) khác \(A,B\)). Từ \(I\), vẽ tiếp tuyến thứ ba của đường tròn \(\left(O\right)\), tiếp tuyến đó cắt \(MA,MB\) tại \(E,F\). Cho \(\hat{AOB}=120^o\), tìm giá trị nhỏ nhất của \(S_{OEF}\).
Cho đường tròn left(O;Rright) và 2 đường kính AB và CD sao cho tiếp tuyến tại A của đường tròn left(O;Rright) cắt các đường thẳng BC và BD tại hai điểm tương ứng là E và F. Gọi P và Q lần lượt là trung điểm của các đoạn thẳng AE và AF.
a) Chứng minh rằng trực tâm H của tam giác BPQ là trung điểm của đoạn thẳng OA.
b) Gọi alpha là số đo góc BFE. Hai đường kính AB và CD thỏa mãn điều kiện gì thì biểu thức: Psin^6alpha+cos^6alpha đạt giá trị nhỏ nhất? Tìm giá trị nhỏ nhất đó.
c) Chứng minh các hệ...
Đọc tiếp
Cho đường tròn \(\left(O;R\right)\) và 2 đường kính \(AB\) và \(CD\) sao cho tiếp tuyến tại \(A\) của đường tròn \(\left(O;R\right)\) cắt các đường thẳng \(BC\) và \(BD\) tại hai điểm tương ứng là \(E\) và \(F\). Gọi \(P\) và \(Q\) lần lượt là trung điểm của các đoạn thẳng \(AE\) và \(AF\).
\(a\)) Chứng minh rằng trực tâm \(H\) của tam giác \(BPQ\) là trung điểm của đoạn thẳng \(OA\).
\(b\)) Gọi \(\alpha\) là số đo góc \(BFE\). Hai đường kính \(AB\) và \(CD\) thỏa mãn điều kiện gì thì biểu thức: \(P=\sin^6\alpha+\cos^6\alpha\) đạt giá trị nhỏ nhất? Tìm giá trị nhỏ nhất đó.
\(c\)) Chứng minh các hệ thức sau: \(CE\cdot DF\cdot EF=CD^3\) và \(\dfrac{BE^3}{BF^3}=\dfrac{CE}{DF}\)
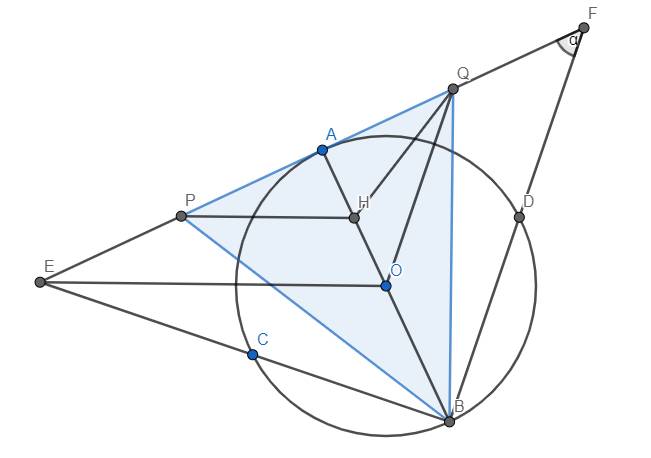
a) Định nghĩa lại H là trung điểm OA. Ta thấy OQ là đường trung bình của tam giác ABF nên OQ//BF. Hơn nữa \(BF\perp BE\) nên \(OQ\perp BE\). Lại có \(BA\perp QE\) nên O là trực tâm của tam giác BEQ \(\Rightarrow OE\perp BQ\)
Mặt khác, PH là đường trung bình của tam giác AOE nên PH//OA. Do đó, \(PH\perp BQ\). Lại thấy rằng \(BH\perp PQ\) nên H là trực tâm tam giác BPQ (đpcm)
b) Ta có \(P=\sin^6\alpha+\cos^6\alpha\)
\(=\left(\sin^2\alpha\right)^3+\left(\cos^2\alpha\right)^3\)
\(=\left(\sin^2\alpha+\cos^2\alpha\right)\left(\sin^4\alpha+\cos^4\alpha-\sin^2\alpha\cos^2\alpha\right)\)
\(=1.\left[\left(\sin^2\alpha+\cos^2\alpha\right)^2-3\sin^2\alpha\cos^2\alpha\right]\)
\(=1-3\sin^2\alpha\cos^2\alpha\)
\(\le1-3.\dfrac{\left(\sin^2\alpha+\cos^2\alpha\right)^2}{4}\)
\(=\dfrac{1}{4}\)
Dấu "=" xảy ra \(\Leftrightarrow\sin\alpha=\cos\alpha\) \(\Leftrightarrow\alpha=45^o\) hay 2 dây AB, CD vuông góc với nhau.
Vậy \(min_P=\dfrac{1}{4}\)
c) Ta có \(\left\{{}\begin{matrix}EC.EB=EA^2\\FD.FB=FA^2\end{matrix}\right.\) (hệ thức lượng trong tam giác vuông)
\(\Rightarrow EC.EB.FD.FB=\left(EA.FA\right)^2\)
\(\Rightarrow EC.FD.\left(EB.DB\right)=AB^4\)
\(\Rightarrow EC.FD.\left(EF.AB\right)=AB^4\)
\(\Rightarrow EC.FD.EF=AB^3=CD^3\) (đpcm)
Ta có \(EC.DF=AC.AD=BC.BD\)
\(\Rightarrow\dfrac{EC}{DF}=\dfrac{BC.BD}{DF^2}\)
\(=\dfrac{BC}{DF}.\dfrac{BD}{DF}\)
\(=\dfrac{BE}{BF}.\dfrac{AC}{DF}\)
\(=\dfrac{BE}{BF}.\dfrac{AE}{AF}\)
\(=\left(\dfrac{BE}{BF}\right)^3\)
Ta có đpcm.
Bài khá căng đấy
Đúng 1
Bình luận (0)
Cho BC là một dây của đường tròn left(O;Rright) left(BCne2Rright). Một điểm A thuộc đường tròn sao cho O nằm trong tam giác ABC. Các đường cao AD,BE,CF cắt nhau tại H.
a) Chứng minh rằng: AEcdot ACABcdot AF.
b) Chứng minh rằng: Tam giác AEF đồng dạng với tam giác ABC.
c) Gọi A là trung điểm của BC. Chứng minh rằng AH2cdot AO.
Đọc tiếp
Cho \(BC\) là một dây của đường tròn \(\left(O;R\right)\) \(\left(BC\ne2R\right)\). Một điểm \(A\) thuộc đường tròn sao cho \(O\) nằm trong tam giác \(ABC\). Các đường cao \(AD,BE,CF\) cắt nhau tại \(H\).
\(a\)) Chứng minh rằng: \(AE\cdot AC=AB\cdot AF\).
\(b\)) Chứng minh rằng: Tam giác \(AEF\) đồng dạng với tam giác \(ABC\).
\(c\)) Gọi \(A'\) là trung điểm của \(BC\). Chứng minh rằng \(AH=2\cdot A'O\).

a) Xét 2 tam giác ABE và ACF, ta có:
\(\widehat{AEB}=\widehat{ACF}=90^o\) và \(\widehat{A}\) chung
nên \(\Delta ABE~\Delta ACF\left(g.g\right)\) \(\Rightarrow\dfrac{AB}{AC}=\dfrac{AE}{AF}\) \(\Rightarrow AB.AF=AC.AE\) (đpcm)
b) Từ \(AB.AF=AC.AE\Rightarrow\dfrac{AE}{AB}=\dfrac{AF}{AC}\). Từ đó dễ dàng chứng minh \(\Delta AEF~\Delta ABC\left(c.g.c\right)\)
c) Kẻ đường kính AP của (O). Ta có \(\left\{{}\begin{matrix}AB\perp BP\\AB\perp HC\end{matrix}\right.\) \(\Rightarrow\) BP//HC
CMTT, ta có CP//HB, dẫn đến tứ giác BHCP là hình bình hành. Lại có A' là trung điểm BC \(\Rightarrow\) A' cũng là trung điểm HP.
Do đó OA' là đường trung bình của tam giác PAH \(\Rightarrow AH=2A'O\left(đpcm\right)\)
Đúng 2
Bình luận (0)
Trong mặt phẳng (Oxy) cho đường tròn \(\left(C\right):\left(x-2\right)^2+\left(y-1\right)^2=1\) .
Viết phương trình của đường tròn (C') là ảnh của (C) qua phép \(Q_{\left(O;120^0\right)}\)
Cho hai đường tròn đồng tâm (O;R) và (O;r) với R > r. Từ một điểm P ở trên đường tròn (O ; R), kẻ hai tia Px, Py không qua O cắt hai đường tròn theo thứ tự ở A, B, E và C, D, F. Biết rằng AB > CD. Chứng minh rằng:
a) PA = BE;
b) So sánh các cung nhỏ PE, PF.
a) Xét 2 TH:
- TH \(P_x,P_y\) nằm về 2 phía của đường kính kẻ qua P ( TH còn lại tương tự)
Kẻ \(OI\perp P_x\) ta có:
\(IP=IE,IA=IB\)
\(\Rightarrow PI-AI=EI-BI\) hay PA=BE ( đpcm)
b) Kẻ \(OK\perp P_y\)
Trong đường tròn \(\left(O;r\right)\), vì AB>CD => OI<OK
Khi đó trong đường tròn \(\Rightarrow PE>PF\)
Theo định lý về mối quan hệ giữa dây và cung , trong đường tròn \(\left(O;R\right)\)
ta có: cung PE > cung PF ( đpcm)
Giải :
a) kẻ OH vuông góc với PE bà AB
⇒ H là trđ PE, AB
hay HP = HE, HA = HB
⇒ HP - HA = HE - HB
⇒ AP = BE.
b) kẻ OK vuông góc với PF
-Xét (O;r) có : AB > CD ( gt)
⇒ OH < OK ( mối liên hệ giữa dây và k/c từ tâm đến dây )
-Xét (O;R) có : OH < OK (cmt )
⇒ PE> PF.
a) CM ĐƯỢC IA = IB , IP=IE => PA=BE
b) VÌ AB> CD => OI<OK => PE>PF => CUNG PE > CUNG PF
Xem thêm câu trả lời
























