Cho tam giác ABC, M là trung điểm cạnh BC. C/m \(\frac{AB+AC-BC}{2}

Những câu hỏi liên quan
Cho tam giác ABC, M là trung điểm cạnh BC. cmr:
\(\frac{AB+AC-BC}{2}< AM< \frac{AB+AC}{2}\)
Trên tia đối của MA lấy điểm D sao cho MA = MD
Xét \(\Delta ABM\) và \(\Delta DCM\) có:
\(BM=CM\left(gt\right)\)
\(\widehat{AMB}=\widehat{DMC}\) (đối đỉnh)
\(MA=MD\) (cách vẽ)
\(\Rightarrow\Delta ABM=\Delta DCM\left(c.g.c\right)\)
\(\Rightarrow AB=CD\)(2 cạnh tương ứng)
Xét \(\Delta ACD\) có: \(AD< AC+CD\)
\(\Rightarrow2AM< AC+AB\)
\(\Rightarrow AM< \frac{AB+AC}{2}\left(1\right)\)
Xét \(\Delta MAB\)có: \(AM>AB-BM\)
Xét \(\Delta MAC\)có: \(AM>AC-MC\)
\(\Rightarrow AM+AM>AB-BM+AC-MC\)
\(\Rightarrow2AM>AB+AC-\left(BM+CM\right)\)
\(\Rightarrow2AM>AB+AC-BC\)
\(\Rightarrow AM>\frac{AB+AC-BC}{2}\left(2\right)\)
Từ (1) và (2) => \(\frac{AB+AC-BC}{2}< AM< \frac{AB+AC}{2}\left(đpcm\right)\)
Đúng 0
Bình luận (0)
Cho \(M,N\) lần lượt là trung điểm của hai cạnh \(AB;AC\) của tam giác \(ABC\).
a) Tính các tỉ số \(\frac{{AM}}{{AB}},\frac{{AN}}{{AC}}\);
b) Chứng mình \(MN//BC\);
c) Chứng minh \(\frac{{MN}}{{BC}} = \frac{1}{2}\).
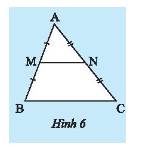
a) Vì \(AM = MB \Rightarrow M\) là trung điểm của \(AB\) (do \(M\) thuộc \(AB\))
\( \Rightarrow AM = \frac{1}{2}AB \Leftrightarrow \frac{{AM}}{{AB}} = \frac{1}{2}\);
Vì \(AN = NC \Rightarrow N\) là trung điểm của \(AC\) (do \(N\) thuộc \(AC\))
\( \Rightarrow AN = \frac{1}{2}AC \Leftrightarrow \frac{{AN}}{{AC}} = \frac{1}{2}\).
b) Vì \(\frac{{AM}}{{AB}} = \frac{1}{2};\frac{{AN}}{{AC}} = \frac{1}{2} \Rightarrow \frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\).
Xét tam giác \(ABC\) có \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\) nên áp dụng định lí Thales đảo ta được \(MN//BC\).
c) Xét tam giác \(ABC\) có \(MN//BC\) nên áp dụng hệ quả định lí Thales ta được \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}}\)
Mà \(\frac{{AM}}{{AB}} = \frac{1}{2} \Rightarrow \frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}} = \frac{1}{2}\).
Vậy \(\frac{{MN}}{{BC}} = \frac{1}{2}\) (điều phải chứng minh).
Đúng 0
Bình luận (0)
Cho tam giác ABC, điểm M là trung điểm của AC. Từ M kẻ đường song song với Bc cắt AB tại điểm N. Hãy chứng tỏ rằng:
a) Diện tích tam giác BNC bằng 1/2 diện tích tam giác ABC
b) N là trung điểm của AB
c) Cạnh MN bằng 1/2 cạnh BC
Cho tam giác ABC , M là trung điểm của AB, N là trung điểm của cạnh AC. Trên tia MN lấy điểm P sao cho N là trung điểm của MP. CMR
a/ tam giác BMC= tam giác PCM
b/MN//BC và MN=\(\frac{1}{2}\)BC
cho tam giác ABC có AB=AC trên các cạnh AB vf AC lấy tương ứng 2 điểm D và E sao cho AD=AE gọi M là trung điểm của BC.
a. C/M DE//BC
b. tam giác MBD=tam giác MCE
c. tam giác AMD=tam giác AME
Cho tam giác ABC vuông tại A(AB>AC). M là trung điểm cạnh BC . Trên tia đối của tia MA lấy điểm D sao cho MD=MA. C/m rang a) tam giác MAB= TAM GIÁC MDC b) AB// CD c) AM= 1/2 BC
Bn tự vẽ hình nha!!!
a) Xét \(\Delta ABM\) và \(\Delta DCM\) có:
MB = MC (M là trung điểm BC (gt))
\(\widehat{AMB} = \widehat{DMC}\)(đối đỉnh)
MA = MD (gt)
\(\Rightarrow\)\(\Delta ABM = \Delta DCM (cgc)\)
b) Vì \(\Delta ABM = \Delta DCM (cmt)\)
\(\Rightarrow\)\(\widehat{BAM} = \widehat{CDM}\) (2 góc tương ứng)
mà 2 góc này nằm ở vị trí so le trong
\(\Rightarrow\) AB // CD
c) Vì \(\Delta ABM = \Delta DCM (cmt)\)
\(\Rightarrow\) AB = DC (2 cạnh tương ứng)Vì AB // CD (cmt)\(AB \perp AC \)\(\Rightarrow\) \(CD \perp AC\) (Định lí 2 bài từ vuông góc đến song song)Xét \(\Delta ABC\) và \(\Delta CDA\) có:\(\widehat{BAC} = \widehat{DCA} = 90^0 \)AB = CD (cmt)AC chung\(\Rightarrow\)\(\Delta ABC = \Delta CDA\) (2 cạnh góc vuông)\(\Rightarrow\) AD = BC (2 cạnh tương ứng)mà \(AM=\frac{1}{2}AD\)\(\Rightarrow AM=\frac{1}{2}BC\)
Đúng 1
Bình luận (1)
cho tam giác ABC có AB=AC trên các cạnh AB vf AC lấy tương ứng 2 điểm D và E sao cho AD=AE gọi M là trung điểm của BC.
a. C/M DE//BC
b. tam giác MBD=tam giác MCE
c. tam giác AMD=tam giác AME
Cho tam giác ABC vuông tại A có AB=3cm,BC=5cm,AC=4cm.Trên tia đối của tia AB lấy điểm M sao cho AB=AM a,so sánh các góc của tam giác ABC b,Chứng minh tam giác BCM cân c,M là trung điểm của cạnh BC,BN cắt AC ở I,MI cắt BC tại H.Chứng minh M,I,H thẳng hàng d,Chứng minh BN+MH+CA< BM+BC+CM Giúp em vớiii,gấp lắm rồi ạaa😭
a: AB<AC<BC
=>góc C<góc B<góc A
b: Xét ΔCBM có
CA vừa là đường cao, vừa là trung tuyến
=>ΔCBM cân tại C
c: N ở đâu vậy bạn?
Đúng 0
Bình luận (0)
cho tam giác ABC vuống tại A với \(\frac{AB}{AC}\)=\(\frac{3}{4}\) và BC= 10 cm a, tính AB;AC b,trên cạnh AC lấy điểm E sao cho AE=2cm , trên tia đối của tia AB lấy điểm D sao cho AD=AB. c/m tam giác BEC= tam giác DEC c, c/m DE đi qua trung diểm cạn BC













