Điểm I nằm trên đoạn thẳng BC và 3IB=2IC. Vậy BC/IC
giúp với
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Cho n là 1 số tự nhiên không chia hết cho 3.Số dư của \(n^{2016}\)khi chia cho 13 là bao nhiêu ?
Điểm I trên đoạn thẳng BC và 3IB=2IC. Vậy tỉ số \(\dfrac{BC}{IC}\)bằng bao nhiêu?
3IB = 2TC
IB/2 = IC/3 = TB + IC/ 2+3 = BC/5
TC/3 = BC/5 = BC/IC = 5/3
Bn bảng A hay bảng B thế???
I thuộc BC ; 3IB = 2IC . Vậy BC/IC =
Giải giúp mình nhé :)))
Có :
\(IB=IC=BC\)
\(3IB=2IC\)
\(\Rightarrow\frac{IB}{2}=\frac{IC}{3}\)
Đặt \(\frac{IB}{2}=\frac{IC}{3}=k\Rightarrow IC=3k\)
\(IB=2k\)
\(BC=3k+2k=5k\)
\(\Rightarrow\frac{BC}{IC}=\frac{5k}{3k}=\frac{5}{3}\)
Cho n là 1 số tự nhiên không chia hết cho 3.Số dư của \(n^{2016}\)khi chia cho 13 là bao nhiêu ?
Điểm I trên đoạn thẳng BC và 3IB=2IC. Vậy tỉ số \(\dfrac{BC}{IC}\)bằng bao nhiêu?
* ta có 3IB=2IC =>\(\dfrac{IB}{2}=\dfrac{IC}{3}\)
Vì I nằm trên đoạn thẳng BC =>\(\dfrac{IB}{2}=\dfrac{IC}{3}=\dfrac{IB+IC}{2+3}=\dfrac{BC}{5}\)
*\(\dfrac{IC}{3}=\dfrac{BC}{5}\)=>\(\dfrac{BC}{IC}=\dfrac{5}{3}\)
Cho n là 1 số tự nhiên không chia hết cho 3.Số dư của \(n^{2016}\)khi chia cho 13 là bao nhiêu ?
Điểm I trên đoạn thẳng BC và 3IB=2IC. Vậy tỉ số \(\dfrac{BC}{IC}\)bằng bao nhiêu?
3IB=2IC
nên IB=2/3IC
IB+IC=BC
=>2/3IC+IC=BC
=>5/3IC=BC
=>5IC=3BC
=>BC/IC=5/3
Cho tam giác ABC có AB=8a, AC=6a, BC=4a. Gọi D là trung điểm AB và I là điểm
thỏa mãn IA+3IB-2IC=0 Tìm tập hợp các điểm M thỏa mãn \(MA^2+3MB^2-2MC^2=24a^2\)
Điểm F nằm trên đường thảng BC VÀ BÊN ngoài đoạn thẳng BC. sao cho 5.FB=2.FC. Vậy tỉ số FB/BC=.....
Trên nửa mặt phẳng bờ m lấy hai điểm A và B, trên nửa mặt phẳng đối lấy điểm C (A, B,C ∉ a).
a) Chứng tỏ rằng hai đoạn thẳng AC và BC cắt đường thẳng m.
b) Gọi I và K lần lượt là giao điểm của đoạn thẳng AC, BC với đường thẳng m. Chứng tỏ rằng tia AK nằm giữa hai tia AB và AC, tia BI nằm giữa hai tia BA và BC.
c*) Giải thích tại sao hai đoạn thẳng AK và BI cắt nhau?
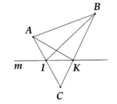
a) Vì hai điểm A, B nằm trên hai nửa mặt phẳng đối nhau bờ m nên đoạn thẳng AB cắt đường thẳng m.
b) Từ câu a), ta suy ra điểm K nằm giữa hai điểm B, C nên tia AK nằm giữa hai tia AB và AC.
Tương tự, ta có điểm I nằm giữa hai điểm A, C nên tia BI nằm giữa, hai tia BA, BC.
c*) Từ câu b), ta suy ra tia BI nằm giữa hai tia BA,BK nên tia BI cắt đoạn thẳng AK tại một điểm nằm giữa A và K.
Lập luận tương tự, ta có tia AK cắt đoạn thẳng BI tại một điểm nằm giữa B và I. Từ đó suy ra hai đoạn thẳng AK và BI cắt nhau.
Cho tứ diện ABCD. Gọi G là trọng tâm của tam giác ABD, điểm I nằm trên cạnh BC sao cho BI=2IC. Chứng minh rằng IG song song với mặt phẳng (ACD).
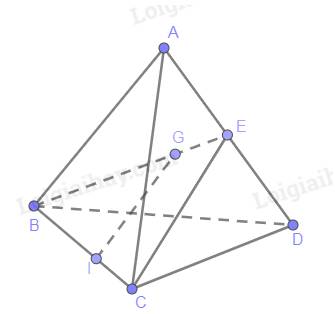
Tam giác BCE có E là trung điểm AD
Suy ra:\(\frac{{BG}}{{BE}} = \frac{{BI}}{{BC}} = \frac{2}{3}\)
Theo Ta lét, IG //CE
Mà CE thuộc (ACD)
Suy ra: IG // (ACD)
cho đoạn thẳng BC= 6cm và điểm I là trung điểm của BC
1) tính độ dài các đoạn thẳng IB và IC
2) cho điểm D trên đường thẳng BC và cách điểm một đoạn 10 cm ( C nằm giữa B và I)
a) tính độ dài đoạn thẳng CD
b) tính độ dài đoạn thẳng ID
1, Trên đoạn thẳng BC, có:
I là trung điểm của BC
IB=IC=BC\2=6\2=3 (cm)
2,? vì bạn ko nói cách điểm B,C hay I.