Mặt đứng là hình chiếu vuông góc của mặt ngoài ngôi nhà nên :
Mặt phẳng chiếu đứng
Mặt phẳng chiếu cạnh hoặc MP chiếu bằng
Mặt phẳng chiếu đứng hoặc MP chiếu cạnh
Mặt phẳng chiếu bằng
Mặt đứng là hình chiếu vuông góc của mặt ngoài ngôi nhà nên :
Mặt phẳng chiếu đứng
Mặt phẳng chiếu cạnh hoặc MP chiếu bằng
Mặt phẳng chiếu đứng hoặc MP chiếu cạnh
Mặt phẳng chiếu bằng
Mặt đứng là hình chiếu vuông góc của mặt ngoài ngôi nhà lên:
A. Mặt phẳng chiếu đứng
B. Mặt phẳng chiếu cạnh
C. Cả A và B đều đúng
D. Đáp án khác
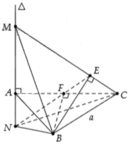
Cho tam giác đều ABC có cạnh bằng a, trên đường thẳng ∆ đi qua A vuông góc với mặt phẳng (ABC) lấy điểm M bất kì. Gọi E, F lần lượt là hình chiếu vuông góc của B lên MC, AC và đường thẳng ∆ cắt EF tại N (như hình bên). Khi đó thể tích của tứ diện MNBC đạt giá trị nhỏ nhất bằng bao nhiêu?
A. a 3 6 4 .
B. a 3 3 4 .
C. a 3 3 6 .
D. a 3 6 12 .
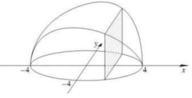
Một vật có kích thước và hình dáng như hình vẽ dưới đây. Đáy là hình tròn giới hạn bởi đường tròn x 2 + y 2 = 16 (nằm trong mặt phẳng Oxy), cắt vật bởi các mặt phẳng vuông góc với trục Ox ta được thiết diện là hình vuông. Thể tích của vật thể là
A. ∫ − 1 4 4 16 − x 2 d x
B. ∫ − 4 4 4 π x 2 d x
C. ∫ − 4 4 4 x 2 d x
D. ∫ − 4 4 4 π 16 − x 2 d x
khi mặt đáy của hình nón cụt đặt vuông góc với mặt phẳng nằm ngang thì
(2.5 Điểm)
hình chiếu đứng là hình tròn
hình chiếu đứng là hình thang cân
hình chiếu bằng là hình tròn
hình chiếu cạnh là hình tròn
Câu 17: Là hình cắt mặt bằng của ngôi nhà, nhằm diễn tả vị trí, kích thước các tường, vách, cửa đi, cửa sổ, các thiết bị, đồ đạc… là nội dung nào của bản vẽ nhà?
A. Hình chiếu
B. Mặt đứng
C. Mặt cắt A - A
D. Mặt bằng
Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2 2 , cạnh bên SA vuông góc với mặt phẳng đáy. Mặt phẳng ( α ) qua A và vuông góc với SC cắt cạnh SB, SC, SD lần lượt tại các điểm M, N, P. Thể tích V của khối cầu ngoại tiếp tứ diện CMNP bằng
![]()
![]()
![]()
![]()
Cho hình chóp S.ABCD có đáy là hình thoi tâm với BAD = 1200 và BD = a. Cạnh bên SA vuông góc với đáy. Góc giữa mặt (SBC) và đáy bằng 600. Mặt phẳng (P) đi qua BD và vuông góc với cạnh SC. Tính tỉ số thể tích giữa hai phần của hình chóp do mặt phẳng (P) tạo ra khi cắt hình chóp?

A. 10
B. 11
C. 12
D. 13
Đáp án D
Từ O kẻ OH vuông góc với SC, ta có S C ⊥ ( B D H )
Ta có V S . A H D V S . A C D = S H S C , V S . A H B V S . A C B = S H S C
mà V S . A C D = V S . A C B = 1 2 V S . A B C D = V 2
nên V S . A H D + V S . A H B V 2 = 2 S H S C
⇔ V S . A B H D V = S H S C
Có
B
C
⊥
(
S
A
M
)
nên
![]()
⇒ S A = 3 a 2
Mặt khác: ∆ C A S ~ ∆ C H O
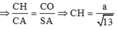
Suy ra S H S C = S C - H C S C = 1 - H C S C = 11 13
⇒ V S . A B H D = 11 13 V
Do đó
V H . B C D = V - V S . A B H D = V = 11 12 V = 2 13 V
Cho khối chóp S.ABCD có đáy ABCD là hình chữ nhật. Một mặt phẳng thay đổi nhưng luôn song song với đáy và cắt các cạnh bên SA,SB,SC,SD lần lượt tại M,N,P,Q. Gọi M',N',P',Q' lần lượt là hình chiếu vuông góc của M, N, P, Q lên mặt phẳng (ABCD). Tỉ số SM/SA bằng bao nhiêu để thể tích khối đa diện MNPQ.M’N’P’Q’ đạt giá trị lớn nhất.
A. 2 3
B. 1 2
C. 1 3
D. 3 4
Bạn An đang học vẽ hình bằng phần mềm máy tính. An vẽ hình một ngôi nhà với phần mái có dạng hình tam giác cân (hình vẽ bên). Biết góc tạo bởi phần mái và mặt phẳng nằm ngang là 30 0 , chiều dài mỗi bên dốc mái là 3,5m. Tính gần đúng bề rộng của mái nhà.
A. 6,52m
B. 6,06m
C. 5,86m
D. 5,38m
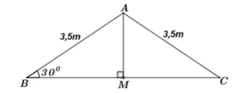
Ta vẽ lại mô hình mái nhà như hình vẽ bên.
Theo đề bài cho ta có: ∆ ABC cân tại A
![]()
Thì khi đó bề rộng mái nhà chính là độ dài cạnh BC.
Gọi M là trung điểm của BC.
=> AM là đường trung tuyến đồng thời là đường cao của ABC (tính chất).
Xét ∆ ABM vuông tại M ta có:
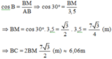
Vậy bề rộng mái nhà là 6,06m
Đáp án cần chọn là: B