Hệ phương trình
(m+1)x-y=m+1x+(m-1)y=2có nghiệm là x0;y0
Giá trị nhỏ nhất S= x0+y0
Cho hệ phương trình 3 x − y = 2 m + 1 x + 2 y = − m + 2 (m là tham số). Tìm m để hệ có nghiệm duy nhất (x; y) thỏa mãn x − y = 1
A. m = −1
B. m = 4
C. m = 1
D. m = −2
Ta có
3 x − y = 2 m + 1 x + 2 y = − m + 2 ⇔ 6 x − 2 y = 4 m + 2 x + 2 y = − m + 2 ⇔ 7 x = 3 m + 4 x + 2 y = − m + 2 ⇔ x = 3 m + 4 7 3 m + 4 7 + 2 y = − m + 2 ⇔ x = 3 m + 4 7 2 y = − 7 m + 14 7 − 3 m + 4 7 ⇔ x = 3 m + 4 7 y = − 5 m + 5 7
hệ phương trình có nghiệm duy nhất ( x ; y ) = 3 m + 4 7 ; − 5 m + 5 7
Để x – y = 1 thì 3 m + 4 7 − − 5 m + 5 7 = 1 ⇔ 8m – 1 = 7 ⇔ 8m = 8 m = 1
Vậy với m = 1 thì hệ phương trình có nghiệm duy nhất (x; y) thỏa mãn x − y = 1
Đáp án: C
Với m = 1 thì hệ phương trình x − y = m + 1 x + 2 y = 2 m + 3 có cặp nghiệm (x; y) là:
A. (3; 1)
B. (1; 3)
C. (−1; −3)
D. (−3; −1)
Thay m = 1 vào hệ phương trình đã cho ta được:
x − y = 2 x + 2 y = 5 ⇔ 2 x − 2 y = 4 x + 2 y = 5 ⇔ 3 x = 9 x + 2 y = 5 ⇔ x = 3 y = 1
Vậy hệ phương trình đã cho có nghiệm duy nhất là (3; 1) khi m = 1
Đáp án: A
Với m = 1 thì hệ phương trình x − y = m + 1 x + 2 y = 2 m + 3 có cặp nghiệm (x; y) là:
A. (3; 1)
B. (1; 3)
C. (−1; −3)
D. (−3; −1)
Thay m = 1 vào hệ phương trình đã cho ta được:
x − y = 2 x + 2 y = 5 ⇔ 2 x − 2 y = 4 x + 2 y = 5 ⇔ 3 x = 9 x + 2 y = 5 ⇔ x = 3 y = 1
Đáp án:A
Với m = 1 thì hệ phương trình: x - y = m + 1 x + 2 y = 2 m + 3 có cặp nghiệm (x; y) là:
A. (3; 1)
B. (1; 3)
C. (-1; -3)
D. (-3; -1)
Đáp án A
Thay m = 1 vào hệ phương trình đã cho ta được:
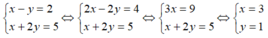
Cho hệ phương trình m − 1 x + y = 2 m x + y = m + 1 (m là tham số). Nghiệm của hệ phương trình khi m = 2 là?
A. (x; y) = (1; −1)
B. (x; y) = (−1; −1)
C. (x; y) = (−1; 1)
D. (x; y) = (1; 1)
Thay m = 2 vào hệ ta được x + y = 2 2 x + y = 3
Khi đó x + y = 2 2 x + y = 3 ⇔ x + y = 2 x = 1 ⇔ x = 1 y = 1
Vậy hệ phương trình có nghiệm duy nhất (1; 1) khi m = 2
Đáp án: D
Cho hệ phương trình m - 1 x + y = 2 m x + y = m + 1 (m là tham số ). Nghiệm của hệ phương trình khi m = 2 là
A. (x; y) = (-1; -1)
B. (x; y) = (1; -1)
C. (x; y) = (-1; 1)
D. (x; y) = (1; 1)
Đáp án D
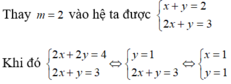
Vậy hệ phương trình có nghiệm duy nhất (1; 1) khi m = 2
Tìm các giá trị của m để nghiệm của hệ phương trình x + 1 4 − y 2 = x + y + 1 x − 2 2 + y − 1 3 = x + y − 1 cũng là nghiệm của phương trình (m + 2)x + 7my = m – 225
A. m = 40
B. m = 5
C. m = 50
D. m = 60
Ta có
x + 1 4 − y 2 = x + y + 1 x − 2 2 + y − 1 3 = x + y − 1
⇔ x + 1 − 2 y = 4 x + 4 y + 4 3 x − 6 + 2 y − 2 = 6 x + 6 y − 6
⇔ 3 x + 6 y = − 3 3 x + 4 y = − 2 ⇔ y = − 1 2 x = 0
Thay x = 0; y = − 1 2 vào phương trình (m + 2)x + 7my = m – 225 ta được:
(m + 2).0 + 7m − 1 2 = m – 225 ⇔ 9 2 m = 225 ⇔ m = 50
Đáp án: C
Cho hệ phương trình m − 1 x + y = 2 m x + y = m + 1 (m là tham số). Kết luận nào sau đây là đúng khi nói về nghiệm (x; y) của hệ phương trình?
A. Hệ phương trình luôn có nguyện duy nhất (x; y) thỏa mãn 2x + y ≤ 3
B. Hệ phương trình luôn có nguyện duy nhất (x; y) thỏa mãn 2x + y > 3
C. Hệ phương trình luôn có nguyện duy nhất (x; y) thỏa mãn 2x + y ≥ 3
D. Hệ phương trình luôn có nguyện duy nhất (x; y) thỏa mãn 2x + y = 3
Từ (m – 1) x + y = 2 thế vào phương trình còn lại ta được phương trình:
mx + 2 – (m – 1) x = m + 1 ⇔ x = m – 1 suy ra y = 2 – ( m – 1 ) 2 với mọi m
Vậy hệ phương trình luôn có nghiệm duy nhất ( x ; y ) = ( m – 1 ; 2 – ( m – 1 ) 2 )
2 x + y = 2 ( m – 1 ) + 2 – ( m – 1 ) 2 = − m 2 + 4 m – 1 = 3 – ( m – 2 ) 2 ≤ 3 với mọi m
Đáp án: A
Cho hệ phương trình x + y = m - 1 x 2 + y 2 - 2 x - 2 y = - 1 . Tìm m để hệ phương trình có nghiệm x 0 ; y 0 thỏa mãn P = x 0 2 + y 0 2 nhỏ nhất
![]()
![]()
![]()
![]()
Cho hệ phương trình: \(\begin{cases} mx + y = 2m - 1\\ (2m + 1)x + 7y=m+3 \end{cases} \)
a. Giải và biện luận hệ phương trình trên
b. Khi hệ có nghiệm (x0; y0). Xác định hệ thức liên hệ giữa x0; y0 không phụ thuộc m