Làm giúp mình 2 bài này với để xíu mình nộp

Những câu hỏi liên quan
Giải giúp mình bài này với ạ giải câu c chi tiết xíu giúp mình với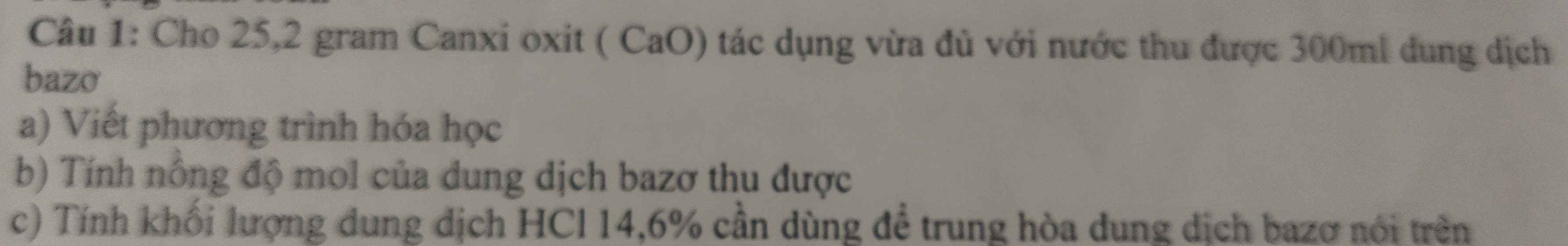
Bạn nào giúp mình làm bài này với 1 tiếng nữa là mình phải nộp rôi
Bạn nào giúp mình làm bài này với 1 tiếng nữa là mình phải nộp rôi
ai giúp mình làm bài này với:
/x-1/ . (y+2) = -6
nhanh lên mai mình phải nộp rùi
vì: | x - 1 | \(\ge\)0
Mà | x - 1 | . ( y + 2 ) = -6
=> | x - 1 | \(\in\left\{1;2;3;6\right\}\)
\(\Rightarrow x+1\in\left\{-6;-3;-2;-1;1;2;3;6\right\}\)
Mà | x - 1 | . ( y + 2 ) = -6
\(\Rightarrow y-2\in\left\{-6;-3;-2;-1;1;2;3;6\right\}\)
Rồi bạn kẻ bảng là được
Đúng 0
Bình luận (0)
Vi /x-1/.(y+20)=-6 nen x-1 va y+2 thuoc U(-6)={1;-1;2-2;3-3;6-6}
Ta co 2 truong hop: x-1<0 ;y+2 >0
x-1>0;y+2 <0
ta xet TH1: x-1 <0 nen x-1=(-x-1) ;y+2>0 nen y+2= y+2
ta co -x-1=-1;y+2=6 -x-1=1; y+2=-6-x-1=-2;y+2=3-x-1=2;y+2=-3VAY THOI CU TU DO MA PHAT TRIEN LEN
Đúng 0
Bình luận (0)
Giải gấp giúp mình 2 bài này với ạ, sáng mai mình nộp rồi. Giúp mình với ạ
Bài 5:
a: BC=10cm
b: HA=4,8cm
HB=3,6(cm)
HC=6,4(cm)
Đúng 0
Bình luận (1)
Bài 6:
\(x^3=6+3\sqrt[3]{\left(3+2\sqrt{2}\right)\left(3-2\sqrt{2}\right)}\left(\sqrt[3]{3+2\sqrt{2}}+\sqrt[3]{3-2\sqrt{2}}\right)\\ \Leftrightarrow x^3=6+3x\sqrt[3]{1}\\ \Leftrightarrow x^3-3x=6\\ y^3=34+3\sqrt[3]{\left(17+12\sqrt{2}\right)\left(17-12\sqrt{2}\right)}\left(\sqrt[3]{17+12\sqrt{2}}+\sqrt[3]{17-12\sqrt{2}}\right)\\ \Leftrightarrow y^3=34+3y\sqrt[3]{1}\\ \Leftrightarrow y^3-3y=34\\ \Leftrightarrow P=x^3-3x+y^3-3y+1980=6+34+1980=2020\)
Đúng 0
Bình luận (0)
ai giúp mình bài toán tìm x này với :3 phần x-1;4 phần x+1;2 nhân x+5 phần x-1(các bạn làm ơn làm nhanh nha để sáng mai vân nộp bài cho thầy giáo nha!)
Bạn nên viết đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để mọi người đọc hiểu đề và hỗ trợ tốt hơn nhé.
Đúng 0
Bình luận (0)
Mọi người ơi giúp mình mấy bài này với (bài khó quá mik làm mãi ko ra mà 8h phải nộp rồi ) giúp mik với huhu

Các bạn làm giúp mình mấy bài này mai mình phải nộp rồi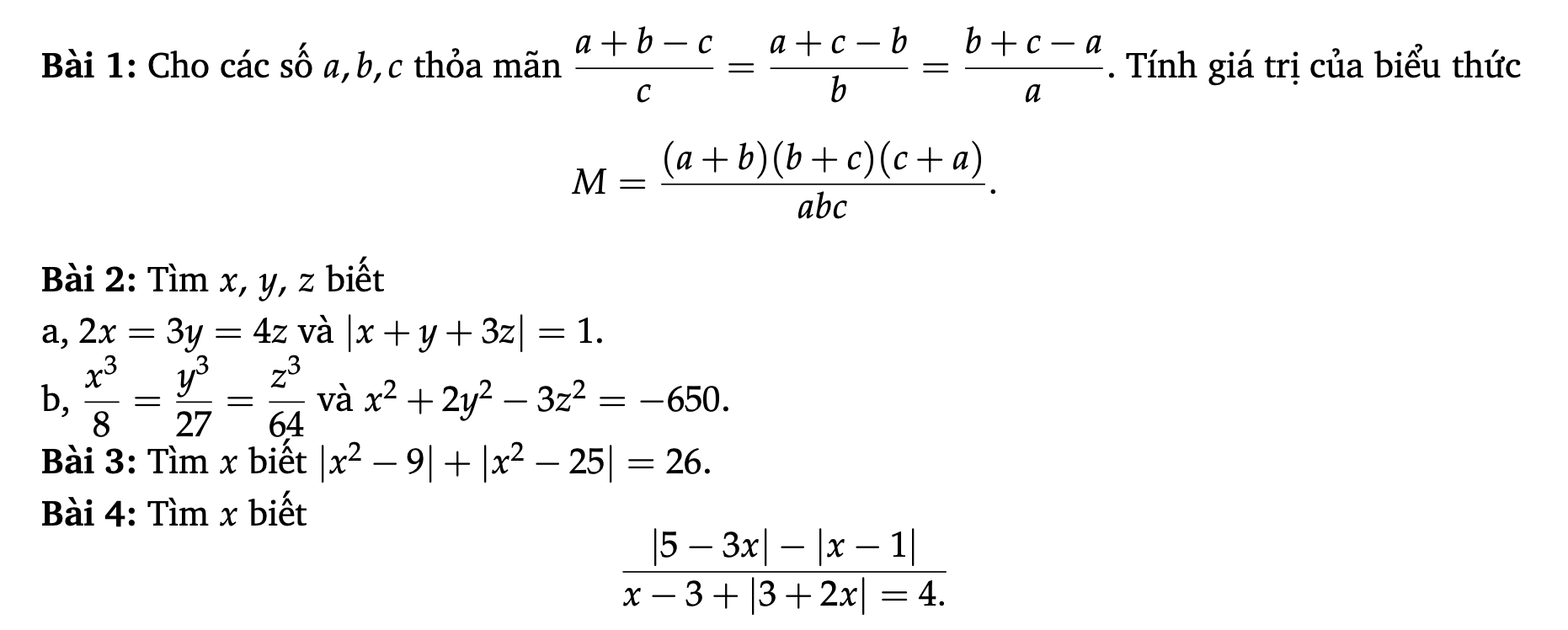
1, \(\dfrac{a+b-c}{c}=\dfrac{a+c-b}{b}=\dfrac{b+c-a}{a}\)
=> \(\dfrac{a+b}{c}-1=\dfrac{a+c}{b}-1=\dfrac{b+c}{a}-1\)
=> \(\dfrac{a+b}{c}=\dfrac{a+c}{b}=\dfrac{b+c}{a}\)
=> \(\dfrac{a+b}{c}=\dfrac{a+c}{b}=\dfrac{b+c}{a}=\dfrac{a+b+a+c+b+c}{a+b+c}=\dfrac{2\left(a+b+c\right)}{a+b+c}=2\)
=> \(M=\dfrac{\left(a+b\right)\left(b+c\right)\left(c+a\right)}{abc}=\dfrac{a+b}{c}\times\dfrac{a+c}{b}\times\dfrac{b+c}{a}=2.2.2=8\)
=> \(M=8\)
Đúng 1
Bình luận (3)
Các bạn làm giúp mình mấy bài này mai mình phải nộp rồi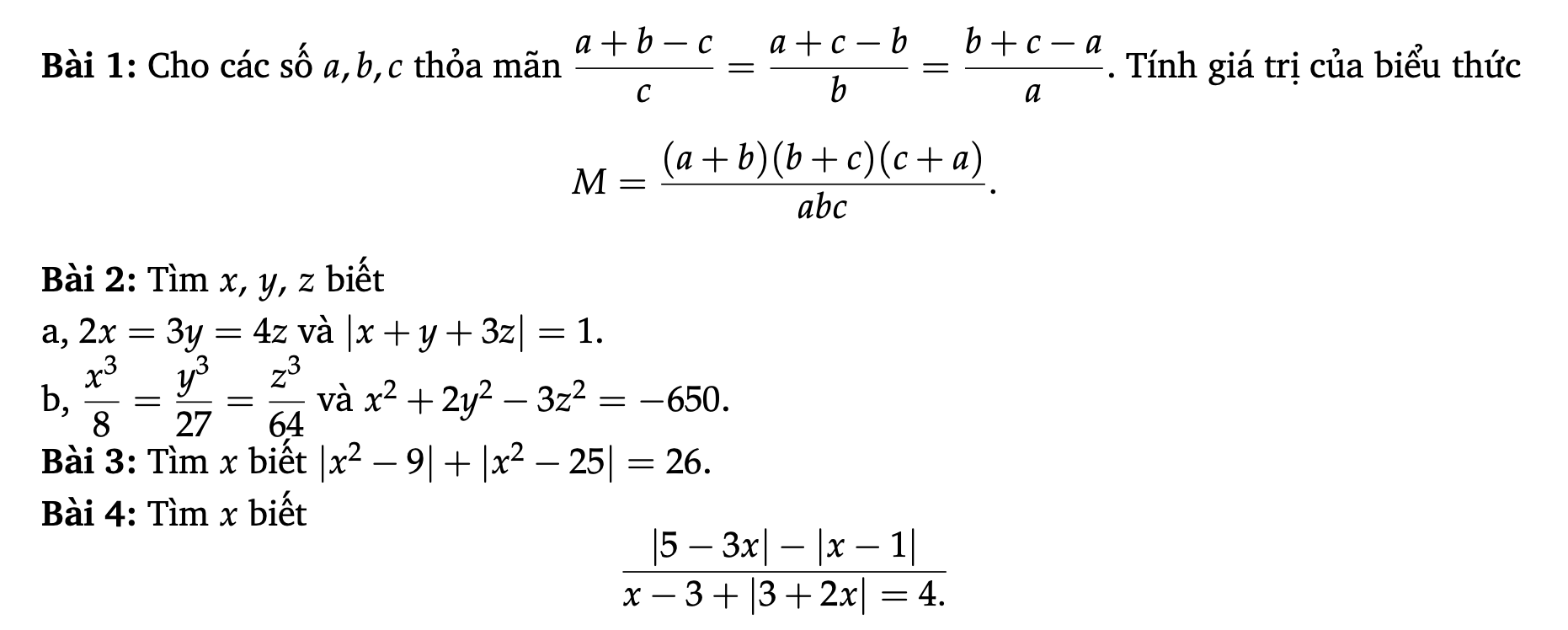
Bài 1:
Nếu $a+b+c=0$ thì đkđb thỏa mãn
$M=\frac{(-c)(-a)(-b)}{abc}=\frac{-(abc)}{abc}=-1$
Nếu $a+b+c\neq 0$. Áp dụng TCDTSBN:
$\frac{a+b-c}{c}=\frac{a+c-b}{b}=\frac{b+c-a}{a}=\frac{a+b-c+a+c-b+b+c-a}{c+b+a}=\frac{a+b+c}{a+b+c}=1$
$\Rightarrow a+b-c=c; a+c-b=b; b+c-a=a$
$\Leftrightarrow a+b=2c; a+c=2b; b+c=2a$
$\Rightarrow a=b=c$
$M=\frac{(a+a)(a+a)(a+a)}{aaa}=\frac{8a^3}{a^3}=8$
Đúng 1
Bình luận (0)
Bài 2a
Đặt $2x=3y=4z=t$
$\Rightarrow x=\frac{t}{2}; y=\frac{t}{3}; z=\frac{t}{4}$
Khi đó:
$|x+y+3z|=1$
$\Leftrightarrow |\frac{t}{2}+\frac{t}{3}+\frac{3t}{4}|=1$
$\Leftrightarrow |\frac{19}{12}t|=1$
$\Rightarrow t=\pm \frac{12}{19}$
Nếu $t=\frac{12}{19}$ thì:
$x=\frac{t}{2}=\frac{6}{19}; y=\frac{4}{19}; z=\frac{3}{19}$
Nếu $t=-\frac{12}{19}$ thì:
$x=\frac{t}{2}=\frac{-6}{19}; y=\frac{-4}{19}; z=\frac{-3}{19}$
Đúng 1
Bình luận (0)
Bài 2b:
$\frac{x^3}{8}=\frac{y^3}{27}=\frac{z^3}{64}$
$\Leftrightarrow (\frac{x}{2})^3=(\frac{y}{3})^3=(\frac{z}{4})^3$
$\Leftrightarrow \frac{x}{2}=\frac{y}{3}=\frac{z}{4}$
Đặt $\frac{x}{2}=\frac{y}{3}=\frac{z}{4}=t$
$\Rightarrow x=2t; y=3t; z=4t$
Khi đó:
$x^2+2y^2-3z^2=-650$
$\Leftrightarrow (2t)^2+2.(3t)^2-3(4t)^2=-650$
$\Leftrightarrow -26t^2=-650$
$\Leftrightarrow t=\pm 5$
Nếu $t=5$ thì:
$x=2t=10; y=3t=15; z=4t=20$
Nếu $t=-5$ thì:
$x=2t=-10; y=3t=-15; z=4t=-20$
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
















