Với x,y,z dương. Không sử dụng bất đẳng thức Cosi. C/m biểu thức sau
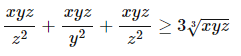
cho x,y,z dương thoả mãn điều kiện : (x+y)(y+z)(z+x)=8xyz.
CMR x=y=z.
Ko dùng bất đẳng thức Cosi.
Cảm ơn.
(x+y)(y+z)(x+z)=8xyz
<=>\((xy+xz+y^2+yz)(x+z)=8xyz\)
<=>\(x^2y+x^2z+y^2z+xyz+xyz+xz^2+z^2y+yz^2=8xyz\)
<=> \(x^2y+x^2z+y^2x+xz^2+y^2z+yz^2-6xyz=0\)
<=> \(y(x^2+z^2-2xz)+x(y^2-2yz+z^2)+z(y^2-2yx+x^2)=0\)
<=>\(y(x-z)^2+x(y-z)^2+z(x-y)^2=0\)
Mà x,y,z dương
=> \((x-z)^2=0=>x=z\)
\((x-y)^2=0=>x=y\)
\((y-z)^2=0=>y=z\)
Vậy x=y=z
Cho a,b,c là các số dương t/m a+b+c=1 a/a+b² + b/b+c² + c/c+a² < hoặc = ¼(1/a + 1/b +1/c) sử dụng bất đẳng thức cosi
=>
=>
=>
Tương tự, ta có:
Do đó, ta có:
(ĐPCM)
Sử dụng bất đẳng thức để viết các mệnh đề sau
a) x là số dương.
b) y là số không âm.
c) Với mọi số thực α, |α| là số không âm.
d) Trung bình cộng của hai số dương a và b không nhỏ hơn trung bình nhân của chúng.
a) x > 0
b) y ≥ 0
c) ∀α ∈ R, |α| ≥ 0
d) ∀a, b > 0, 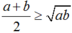
Giúp mk vs mk đg cần gấp!!!
Cho `x,y,z>0` thỏa mãn `x+y+z<=3/2`. Tìm GTNN của biểu thức `A=x^2+y^2+z^2+1/x+1/y+1/z.`
(Sử dụng BĐT Cosi)
Tìm GTLN của \(x\sqrt{a-x^4}\left(x>0\right)\) bằng cách áp dụng bất đẳng thức cosi
Điều kiện \(a>0\)
\(A=\sqrt[4]{\frac{3}{4a}}.\sqrt[4]{\frac{4a}{3}}.x\sqrt{a-x^4}\le\sqrt[4]{\frac{3}{4a}}\left(-x^4+\sqrt{\frac{4a}{3}}x^2+a\right)\)
\(A\le\sqrt[4]{\frac{3}{4a}}\left[\frac{4a}{3}-\left(x^2-\sqrt{\frac{a}{3}}\right)^2\right]\le\frac{4a}{3}\sqrt[4]{\frac{3}{4a}}\)
Dấu "=" xảy ra khi \(x=\sqrt[4]{\frac{a}{3}}\)
Tìm hằng số \(M\) nhỏ nhất để bất đẳng thức sau đúng với mọi \(x,y,z\) không âm:
\(1-xy-yz-zx\le M\left(1-min\left\{x,y,z\right\}\right)\)
P/S: Bài này khá dễ, vì bất đẳng thức này lỏng. Không biết có "cao thủ" nào làm chặt được bất đẳng thức này không ha.
Tìm giá trị lớn nhất của biểu thức A=|x-y|,trong đó \(x^2+4y^2=1\)
SỬ DỤNG BẤT ĐẲNG THỨC BUNHIACOPXKI
MN giúp e với
\(A^2=\left(x-y\right)^2=\left(1.x+\dfrac{1}{2}.\left(-2y\right)\right)^2\le\left(1+\dfrac{1}{4}\right)\left(x^2+4y^2\right)=\dfrac{5}{4}\)
\(\Rightarrow A\le\dfrac{\sqrt{5}}{2}\)
Dấu "=" xảy ra khi \(\left(x;y\right)=\left(-\dfrac{2\sqrt{5}}{5};\dfrac{\sqrt{5}}{10}\right);\left(\dfrac{2\sqrt{5}}{5};-\dfrac{\sqrt{5}}{10}\right)\)
Sử dụng bất đẳng thức liên hệ giữa tổng các nghịch đảo với 2 số dương, tìm Min A biết A=xy+2+\(\dfrac{1}{xy}\) (với x dương nhưng không lớn hơn 1-y).