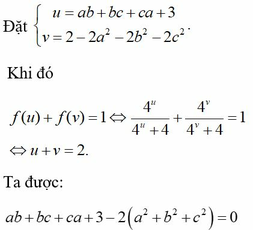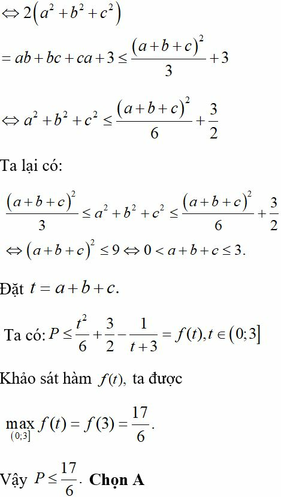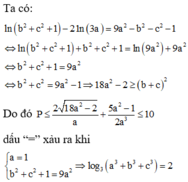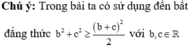cho 3 số a,b,c và thỏa mãn a2=b2+c2 và b2=2c2-8.tính giá trị của M =5a2-7b2-c2

Những câu hỏi liên quan
Cho ba số thực dương a,b,c thỏa mãn
a
2
+
b
2
+
c
2
-
2
a
+
4
b
-
6
c
10
và a + c2 . Tính giá trị biểu thức P 3a + 2b + c khi
Q
a
2
+
b...
Đọc tiếp
Cho ba số thực dương a,b,c thỏa mãn a 2 + b 2 + c 2 - 2 a + 4 b - 6 c = 10 và a + c=2 . Tính giá trị biểu thức P = 3a + 2b + c khi Q = a 2 + b 2 + c 2 - 14 a - 8 b + 18 c đạt giá trị lớn nhất.
A. 10
B. -10
C. 12
D. -12
Đáp án D

Bài toán trở thành: Tìm M nằm trên đường tròn giao tuyến của mặt cầu (S) và mặt phẳng (P) sao cho KM lớn nhất





Đúng 0
Bình luận (0)
Cho các số thực dương a,b,c thỏa mãn
f
a
b
+
b
c
+
c
a
+
3
+
f
2
-
2
a
2
-
2
b
2...
Đọc tiếp
Cho các số thực dương a,b,c thỏa mãn f a b + b c + c a + 3 + f 2 - 2 a 2 - 2 b 2 - 2 c 2 = 1 với hàm số f x = 4 x 4 x + 4 Giá trị lớn nhất của biểu thức P = a 2 + b 2 + c 2 - 1 a + b + c + 3 bằng
A. 17 6
B. 3
C. 13 6
D. 13 4
Cho các số thực a,b,c thỏa mãn a+b+c=0,a2+b2\(\ne\)c2,b2+c2\(\ne\)a2,c2+a2\(\ne\)b2.Tính giá trị biểu thức P=\(\dfrac{a^2}{a^2-b^2-c^2}\)+\(\dfrac{b^2}{b^2-c^2-a^2}\)+\(\dfrac{c^2}{c^2-a^2-b^2}\)
\(\)Ta có: \(a+b+c=0 \Rightarrow b+c=-a \Rightarrow (b+c)^2=(-a)^2 \Leftrightarrow b^2+c^2+2bc=a^2 \Leftrightarrow a^2-b^2-c^2=2bc\)
Tương tự: \(b^2-c^2-a^2=2ca;c^2-a^2-b^2=2ab\)
\(P=...=\dfrac{a^2}{2bc}+\dfrac{b^2}{2ca}+\dfrac{c^2}{2bc}=\dfrac{a^3+b^3+c^3}{2abc}=\dfrac{3abc}{2abc}=\dfrac{3}{2}\)
----
Bổ đề \(a+b+c=0 \Leftrightarrow a^3+b^3+c^3\)
Ở đây ta c/m chiều thuận:
Với \(a+b+c=0 \Leftrightarrow a+b=-c \Rightarrow (a+b)^3=(-c)^3 \Leftrightarrow a^3+b^3+3ab(a+b)=-c^3 \Leftrightarrow a^3+b^3+c^3=3abc(QED)\)
Đúng 0
Bình luận (0)
cho 3 số thực dương không âm thỏa mãn a+b+c1
tìm MAX của P√a2+2b2+√b2+2c2+√c2+2a2
Đọc tiếp
cho 3 số thực dương không âm thỏa mãn a+b+c=1
tìm MAX của
Dấu "=" xảy ra khi và các hoán vị
Đúng 2
Bình luận (0)
Cho a,b,c 0 thỏa mãn
ln
b
2
+
c
2
+
1
-
2
ln
3
a
9
a
2
-
b
2
-
c
2
-...
Đọc tiếp
Cho a,b,c >0 thỏa mãn ln b 2 + c 2 + 1 - 2 ln 3 a = 9 a 2 - b 2 - c 2 - 1 Giá trị lớn nhất của biểu thức P = 2 b + c a + 5 a 2 - 1 2 a 3 đạt tại (x;y;z) Giá trị của log 3 x 3 + y 3 + z 3 là:
A. 2
B. 3
C. 4
D. 5
cho các số a, b, c thỏa mãn a2+b2=c2+d2=2022 và ad+bc=0. Tính giá trị của biểu thức a3b3+c3d3
\(\left(ad+bc\right)\left(a^2d^2+b^2c^2\right)=0\)
\(\Rightarrow a^3d^3+adb^2c^2+bca^2d^2+b^3c^3=0\)
\(\Rightarrow a^3d^3+abcd\left(bc+ad\right)+b^3c^3=0\)
\(\Rightarrow a^3d^3+abcd.0+b^3c^3=0\)
\(\Rightarrow a^3d^3+b^3c^3=0\)
Đúng 2
Bình luận (2)
cho a,b,c thỏa mãn a+b+c=0 và a2=2(a+c+1)(a+b-1). tính giá trị A=a2+b2+c2
Thay \(a=-\left(b+c\right)\) ; \(a+c=-b\) và \(a+b=-c\) vào điều kiện thứ 2 ta có
\(\left(b+c\right)^2=2\left(-b+1\right)\left(-c-1\right)\)
<=> \(b^2+c^2+2bc=2bc+2b-2c-2\)
<=> \(\left(b-1\right)^2+\left(c+1\right)^2=0\) <=> \(\left\{{}\begin{matrix}b=1\\c=-1\end{matrix}\right.\)
suy ra: a=0. Vậy A = a2 + b2 + c2 = 2
Đúng 1
Bình luận (1)
Cho các số thực a,b,c thỏa mãn đồng thời a2+2=b4 , b2+2=c4, c2+2=a4
tĩnh giá trị biểu thức B=a2+b2+c2+a2b2c2-(a2b2+b2c2+c2a2)+2022
Cho các số thực a, b, c thỏa mãn 2.( b2 + bc + c2) = 3.( 3 – a2). Tìm giá trị lớn nhất và nhỏ nhất của biểu thức T = a + b + c
\(9=3a^2+2b^2+2bc+2c^2=\left(a+b+c\right)^2+2a^2+b^2+c^2-2a\left(b+c\right)\)
\(\Rightarrow9\ge\left(a+b+c\right)^2+2a^2+\dfrac{1}{2}\left(b+c\right)^2-2a\left(b+c\right)\)
\(\Rightarrow9\ge\left(a+b+c\right)^2+\dfrac{1}{2}\left(2a-b-c\right)^2\ge\left(a+b+c\right)^2\)
\(\Rightarrow-3\le a+b+c\le3\)
\(T_{max}=3\) khi \(a=b=c=1\)
\(T_{min}=-3\) khi \(a=b=c=-1\)
Đúng 1
Bình luận (1)
cho a,b,c là các số thực thỏa mãn a,b≥0;0≤c≤1 và a2+b2+c2 =3.Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P=ab+bc+ca+3(a+b+c)
\(P\le a^2+b^2+c^2+3\sqrt{3\left(a^2+b^2+c^2\right)}=12\)
\(P_{max}=12\) khi \(a=b=c=1\)
Lại có: \(\left(a+b+c\right)^2=3+2\left(ab+bc+ca\right)\ge3\Rightarrow a+b+c\ge\sqrt{3}\)
\(a+b+c\le\sqrt{3\left(a^2+b^2+c^2\right)}=3\)
\(\Rightarrow\sqrt{3}\le a+b+c\le3\)
\(P=\dfrac{\left(a+b+c\right)^2-\left(a^2+b^2+c^2\right)}{2}+3\left(a+b+c\right)\)
\(P=\dfrac{1}{2}\left(a+b+c\right)^2+3\left(a+b+c\right)-\dfrac{3}{2}\)
Đặt \(a+b+c=x\Rightarrow\sqrt{3}\le x\le3\)
\(P=\dfrac{1}{2}x^2+3x-\dfrac{3}{2}=\dfrac{1}{2}\left(x-\sqrt{3}\right)\left(x+6+\sqrt{3}\right)+3\sqrt{3}\ge3\sqrt{3}\)
\(P_{min}=3\sqrt{3}\) khi \(x=\sqrt{3}\) hay \(\left(a;b;c\right)=\left(0;0;\sqrt{3}\right)\) và hoán vị
Đúng 1
Bình luận (0)