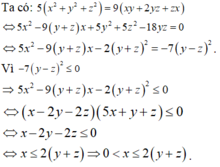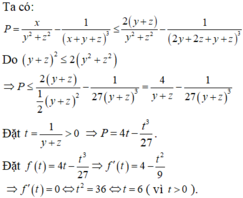Cho các số thực x,y,z thỏa mãn: x+y+z=6.Tìm giá trị lớn nhất của A=xy+2yz+3zx

Những câu hỏi liên quan
cho x,y,z thỏa mãn x+y+z=6. tìm giá trị lớn nhất của A=xy+2yz+3zx
A = xy + 2yz + 3xz = xy + xz + 2yz + 2xz = x(y + z) + 2z(y + z)
Áp dụng BĐT: (a+b)^2/4 ≥ ab dấu = khi a = b
ta có:
(x + y + z)^2/4 ≥ x(y + z)
(x+ y +z)^2/4 ≥ z(y + z)
=> A ≤ 3(x + y + z)^2/4 = 3.36/4 = 27
=>Giá trị lớn nhất của = 27 sẽ xảy ra khi có các trường hợp:
{x = y + z
{z = y + z
Vậy y = 0 và x = z = 3
Đúng 0
Bình luận (0)
\(A=xy+2yz+3zx=x\left(6-x-z\right)+2\left(6-x-z\right)+3zx\)
\(=-x^2+6x-2z^2+12z=\left(-x^2+6x-9\right)+\left(-2z^2+12z-18\right)+27\)
\(=27-\left(x-3\right)^2-2\left(z-3\right)^2\le27\)
Đúng 0
Bình luận (0)
\(A=x\left(6-x-z\right)+2y\left(6-x-z\right)+3zx=-x^2+6x-2z^2+12z\)
\(=\left(-x^2+6x-9\right)+\left(-2z^2+12z-18\right)+27=27-\left(x-3\right)^2-2\left(z-3\right)^2\le27\)
PS: Cai trên ghi thiêu chữ y. Mà thôi coi cai này nè nha.
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho x,y,z là các số thực thỏa mãn xy + yz + 3zx = 1 . Tìm giá trị nhỏ nhất của biểu thức P = x^2 + y^2 + z^2
Đặt \(a=\frac{9+3\sqrt{17}}{4}\) và \(b=\frac{3+\sqrt{17}}{4}\)khi đó \(a=3b\)và \(a+1=2b^2=c=\frac{13+3\sqrt{17}}{4}\)
Áp dụng BĐT AM-GM ta thu được các BĐT sau: \(x^2+b^2y^2\ge2bxy\)
\(by^2+z^2\ge2byz\)
\(a\left(z^2+x^2\right)\ge2azx\)
Cộng các vế theo các vế các BĐT thu được để có:
\(\left(a+1\right)\left(x^2+z^2\right)+2b^2y^2\ge2b\left(xy+yz\right)+2azx\)
Hay \(c\left(x^2+y^2+z^2\right)\ge2b\left(xy+yz+3zx\right)\). Từ đó ta thay các giá trị của \(xy+yz+3zx\); b và c để có được
\(P=x^2+y^2+z^2\ge\frac{\sqrt{17}-3}{2}\)
Cuối cùng, với \(x=z=\frac{1}{\sqrt[4]{17}}\)và \(y=\sqrt{\frac{13\sqrt{17}-51}{34}}\)( Thỏa mãn giả thiết ) thì \(P=\frac{\sqrt{17}-3}{2}\)
Nên ta kết luận \(\frac{\sqrt{17}-3}{2}\)là giá trị nhỏ nhất của biểu thức \(P=x^2+y^2+z^2\)
Đúng 0
Bình luận (0)
cho 3 số thực x, y, z thỏa mãn x+y+z =4,tìm giá trị lớn nhất của biểu thức A = xy+3yz+2zx
\(A=3yz+\left(4-y-z\right)\left(y+2z\right)\)
\(A=-y^2+4y-2z^2+8z\)
\(A=-\left(y-2\right)^2-2\left(z-2\right)^2+12\le12\)
\(A_{max}=12\) khi \(\left(x;y;z\right)=\left(0;2;2\right)\)
Đúng 1
Bình luận (2)
biết các số nguyên dương x, y, z thỏa mãn hệ phương trình :x²+xy+(y²/3)=25, (y²/3)+z²=9, z²+xz+x²=16. tính A=xy+2yz+3zx
de sai roi em oi
o phuong trinh 2 can them +yz nhe
Đúng 0
Bình luận (0)
Cho các số thực x, y, z thỏa mãn: x + y + z = 6. Tìm GTLN của
A= xy +2yz +3xz
\(A=xy+xz+2yz+2xz=x\left(y+z\right)+2z\left(x+y\right)\)
\(=x\left(6-x\right)+2z\left(6-z\right)=-x^2+6x+2\left(-z^2+6z\right)\)
\(=-\left(x-3\right)^2-2\left(z-3\right)^2+27\le27\)
\(A_{max}=27\) khi \(\left(x;y;z\right)=\left(3;0;3\right)\)
Đúng 0
Bình luận (0)
cho x, y, z \(\in\)R thỏa mãn x+y+z=6. tìm GTLN của biểu thức A=xy+2yz+3zx
MÌNH CẦN GẤP Ạ!!!
Cho các số thực dương x, y, z thay đổi và thỏa mãn:
5
x
2
+
y
2
+
z
2
9
x
y
+
2
y...
Đọc tiếp
Cho các số thực dương x, y, z thay đổi và thỏa mãn: 5 x 2 + y 2 + z 2 = 9 x y + 2 y z + z x . Tìm giá trị lớn nhất của biểu thức: P = x y 2 + z 2 - 1 x + y + x 3 bằng
A. 18..
B. 12.
C. 16.
D. 24.
Cho x ,y ,z thỏa mãn : x+ y+z =0 . Chứng minh rằng : xy+2yz+3zx ≤ 0
\(xy+2yz+3zx=xy+zx+2yz+2zx=x\left(y+z\right)+2z\left(y+x\right)=x.\left(-x\right)+2z.\left(-z\right)=-x^2-2z^2\le0\)-Dấu bằng xảy ra \(\Leftrightarrow x=y=z=0\)
Đúng 0
Bình luận (0)
1. Cho x,y,z là ba số dương thay đổi và thỏa mãn ^{x^2+y^2+z^2le xyz}Hãy tìm giá trị lớn nhất của biểu thức Afrac{x}{x^2+yz}+frac{y}{y^2+zx}+frac{z}{z^2+xy}2. Cho x,y,z là các số thực không âm thỏa mãn x^2+y^2+z^23Tìm giá trị lớn nhất của biểu thức Bxy+yz+zx+frac{5}{x+y+z}
Đọc tiếp
1. Cho x,y,z là ba số dương thay đổi và thỏa mãn \(^{x^2+y^2+z^2\le xyz}\)
Hãy tìm giá trị lớn nhất của biểu thức \(A=\frac{x}{x^2+yz}+\frac{y}{y^2+zx}+\frac{z}{z^2+xy}\)
2. Cho x,y,z là các số thực không âm thỏa mãn \(x^2+y^2+z^2=3\)
Tìm giá trị lớn nhất của biểu thức \(B=xy+yz+zx+\frac{5}{x+y+z}\)