Chứng minh rằng:
S2= 32 phần 20*23 + 32 phần 23*26 + 32 phần 2*29 + . . . + 32 phần 77*80 < 1 phần 8
3 mũ 2 phần 20*23+3 mũ 2 phần 23*26+3 mũ 2 phần 26*29 +...+3 mũ 2 phần 77*80
tính nhanh nha
\(\dfrac{3^2}{20.23}+\dfrac{3^2}{23.26}+\dfrac{3^2}{26.29}+...+\dfrac{3^2}{77.80}\)
\(=3\left(\dfrac{3}{20.23}+\dfrac{3}{23.26}+\dfrac{3}{26.29}+...+\dfrac{3}{77.80}\right)\)
\(=3\left(\dfrac{1}{20}-\dfrac{1}{23}+\dfrac{1}{23}-\dfrac{1}{26}+\dfrac{1}{26}-\dfrac{1}{29}+...+\dfrac{1}{77}-\dfrac{1}{80}\right)\)
\(=3\left(\dfrac{1}{20}-\dfrac{1}{80}\right)\)
\(=3\left(\dfrac{4}{80}-\dfrac{1}{80}\right)=3.\dfrac{3}{80}=\dfrac{9}{80}\)
75 phần 100+18 phần 21+19 phần 32+ 1 phần 4+ 3 phần 21+13 phần 23
\(\frac{75}{100}+\frac{18}{21}+\frac{19}{32}+\frac{1}{4}+\frac{3}{21}+\frac{13}{23}=\frac{3}{4}+\frac{6}{7}+\frac{19}{32}+\frac{1}{4}+\frac{1}{7}+\frac{13}{23}\)
\(=\left(\frac{3}{4}+\frac{1}{4}\right)+\left(\frac{6}{7}+\frac{1}{7}\right)+\left(\frac{19}{32}+\frac{13}{23}\right)\)
\(=1+1+\frac{853}{736}\)
\(=2+\frac{853}{736}\)
\(=\frac{2325}{736}\)
21 phần 23 cộng 32 phần 30
\(\dfrac{21}{23}\)+\(\dfrac{32}{30}\)=\(\dfrac{683}{345}\)
\(\frac{21}{23}+\frac{32}{30}=\frac{630}{690}+\frac{736}{690}=\frac{1366}{690}=\frac{683}{345}\)
x là dấu nhân còn X là ích; dấu / là phần nha.VD:1/8 là một phần tám nhé m.n
X x 17/32 + X x 4/23 + 15/32 x X + 19/23 x X =16/32
Mọi người giúp mình nhé,nhớ viết rõ cách giải và kết quả bài toán nhé!Mình sẽ k cho.Thanks nhìu
chứng minh 1phần 2 - 1 phần 4 + 1 phần 8 - 1 phầm 16 + 1 phần 32 - 1 phần 64 + 1 phần 128 - 1 phần 256 < 1 phần 3
\(A=\frac{1}{2}-\frac{1}{4}+\frac{1}{8}-\frac{1}{16}+\frac{1}{32}-\frac{1}{64}+\frac{1}{128}-\frac{1}{256}\)
\(2A=1-\frac{1}{2}+\frac{1}{4}-\frac{1}{8}+\frac{1}{16}-\frac{1}{32}+\frac{1}{64}-\frac{1}{128}\)
\(A+2A=\left(\frac{1}{2}-\frac{1}{4}+...-\frac{1}{256}\right)+\left(1-\frac{1}{2}+\frac{1}{4}-...-\frac{1}{128}\right)\)
\(3A=1-\frac{1}{256}< 1\)
\(\Rightarrow A< \frac{1}{3}\).
A = 1 phần 31 + 1 phần 32 + 1 phần 33 + .... + 1 phần 60
Chứng minh 3 phần 5 < A < 4 phần 5Ta có:
\(A=\left(\dfrac{1}{31}+\dfrac{1}{32}+...+\dfrac{1}{40}\right)+\left(\dfrac{1}{41}+\dfrac{1}{42}+...+\dfrac{1}{50}\right)+\left(\dfrac{1}{51}+\dfrac{1}{52}+...+\dfrac{1}{60}\right)\)
\(A>\dfrac{1}{40}.10+\dfrac{1}{50}.10+\dfrac{1}{60}.10=\dfrac{1}{4}+\dfrac{1}{5}+\dfrac{1}{6}=\dfrac{37}{60}>\dfrac{3}{5}\)
Vậy \(A>\dfrac{3}{5}\)
Ta có:
\(A=\left(\dfrac{1}{31}+\dfrac{1}{32}+...+\dfrac{1}{40}\right)+\left(\dfrac{1}{41}+\dfrac{1}{42}+...+\dfrac{1}{50}\right)+\left(\dfrac{1}{51}+\dfrac{1}{52}+...+\dfrac{1}{60}\right)\)\(A< \dfrac{1}{31}.10+\dfrac{1}{41}.10+\dfrac{1}{51}.10< \dfrac{4}{5}\)
Vậy \(A< \dfrac{4}{5}\)
Do đó: \(\dfrac{3}{5}< A< \dfrac{4}{5}\)
Phần tự luận
Nội dung câu hỏi 1
giải phương trình sau:
x - 3 2 + x + 4 2 = 23 - 3x
x - 3 2 + x + 4 2 = 23 - 3x
⇔ x 2 - 6x + 9 + x 2 + 8x + 16 = 23 - 3x
⇔ 2 x 2 + 5x - 2 = 0
Ta có: a = 2; b = 5; c = -2
Δ = b 2 - 4ac = 5 2 - 4.2.(-2) = 41 > 0
⇒ phương trình đã cho có 2 nghiệm phân biệt
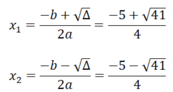
Vậy tập nghiệm của phương trình là
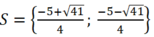
Gồm 5 đơn vị 3 phần mười 4 phần trăm và 2 phần nghìn
Gồm 1 đơn vị 1 phần trăm và 1 phần vạn
Gồm 32 đơn vị 32 phần nghìn và 32 phần triệu
Gồm 2 đơn vị 0,02 đơn vị và 0,0002 đơn vị
Gồm 5 đơn vị 3 phần mười 4 phần trăm và 2 phần nghìn : 5,342
Gồm 1 đơn vị 1 phần trăm và 1 phần vạn: 1,0101
Gồm 32 đơn vị 32 phần nghìn và 32 phần triệu: 32,32000032
Gồm 2 đơn vị 0,02 đơn vị và 0,0002 đơn vị: 2,0202
học tốt
Gồm 5 đơn vị 3 phần mười 4 phần trăm và 2 phần nghìn là: 5,342
Gồm 1 đơn vị 1 phần trăm và 1 phần vạn là: 1,0101
Gồm 32 đơn vị 32 phần nghìn và 32 phần triệu là: 32,32000032
Gồm 2 đơn vị 0,02 đơn vị và 0,0002 đơn vị là: 2,0202
1 phần 2 + 1 phần 4 + 1 phần 8 + 1 phần 16 + 1phan 32
1/2 + 1/4 +1/8 + 1/16 + 1/32
= 16/32 + 3/32 + 4/32 + 2/32 + 1/32
=26/32 =13/16
\(\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}\)
\(=\frac{16}{32}+\frac{8}{32}+\frac{4}{32}+\frac{2}{32}+\frac{1}{32}\)
\(=\frac{31}{32}\)