2. get lucky money

3. talent show

4. always

5. food stands

6. fireworks

7. never

8. eat traditional foods

16A 17B 18B đây nha chị

A

B

B

16A

17B

18B

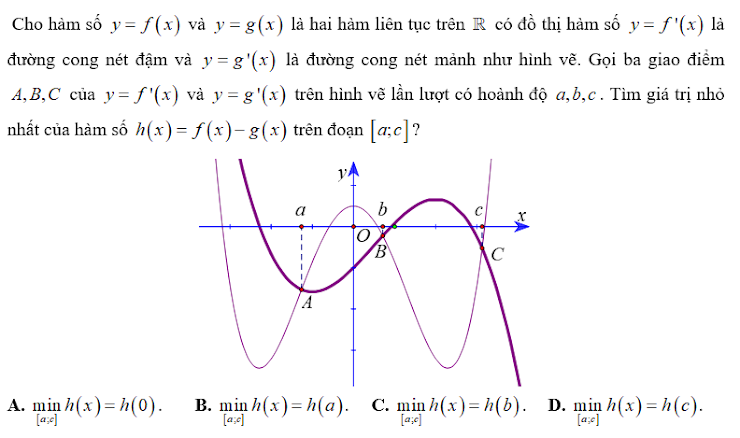
\(h'\left(x\right)=f'\left(x\right)-g'\left(x\right)=0\Rightarrow x=\left\{a;b;c\right\}\)

Ta thấy \(h'\left(x\right)>0\) trên \(\left(b;c\right)\) và \(h'\left(x\right)< 0\) trên \(\left(a;b\right)\)

\(\Rightarrow x=b\) là điểm cực tiểu trên \(\left[a;c\right]\) hay \(\min\limits_{\left[a;c\right]}h\left(x\right)=h\left(b\right)\)

 \(=>Qthu1=0,2.340000=68000J\)

\(=>Qthu2=2100.0,2.20=8400J\)

\(=>Qtoa=2.4200.25=210000J\)

\(=>Qthu1+Qthu2< Qtoa\)=>đá nóng chảy hoàn toàn

\(=>0,2.2100.20+0,2.340000+0,2.4200.tcb=2.4200\left(25-tcb\right)\)

\(=>tcb=14,5^oC\)

Ban can cau nao nhi?

làm bài nào??

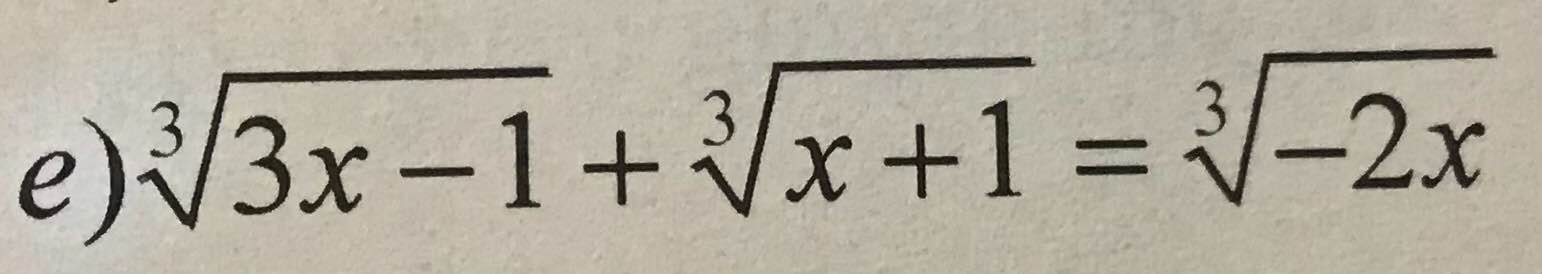
Đặt \(\left\{{}\begin{matrix}\sqrt[3]{3x-1}=a\\\sqrt[3]{x+1}=b\\\sqrt[3]{-2x}=c\end{matrix}\right.\) ta được hệ:

\(\left\{{}\begin{matrix}a+b=c\\a^3+b^3=-2c^3\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}a+b=c\\\left(a+b\right)^3-3ab\left(a+b\right)=-2c^3\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}a+b=c\\c^3-3abc=-2c^3\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}a+b=c\\c\left(c^2-ab\right)=0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}a+b=c\\c\left[\left(a+b\right)^2-ab\right]=0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}a+b=c\\c\left[\left(a+\dfrac{b}{2}\right)^2+\dfrac{3b^2}{4}\right]=0\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}c=0\\a=b=0\left(vn\right)\end{matrix}\right.\)

\(\Rightarrow\sqrt[3]{-2x}=0\Leftrightarrow x=0\)