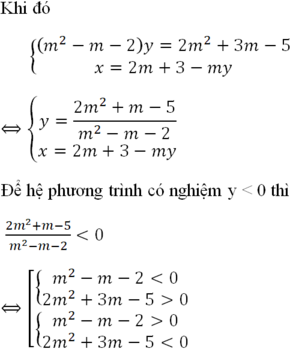hệ số m để phương trình (m + 3)x^2 + mx -2 =0

Những câu hỏi liên quan
cho hệ phương trình x+my=3m
mx-y=m2-2 ( m là tham số)
a. giải phương trình với m=-1
b. tìm m để hệ phương trình có nghiệm (x;y) thỏa mãn (x-1)(m-y),0
a: Thay m=-1 vào hệ phương trình, ta được:
\(\left\{{}\begin{matrix}x-y=3\cdot\left(-1\right)=-3\\-x-y=\left(-1\right)^2-2=-3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-2y=-6\\x-y=-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=3\\x=y-3=3-3=0\end{matrix}\right.\)
Đúng 0
Bình luận (0)
1. Số nghiệm của hệ phương trình hept{begin{cases}x^3+2xy^2+120x^28y^212end{cases}}2. Giá trị nghuyên nhỏ nhất của m để phương trình x^3+mx0có 3 nghiệm riêng biệt.3. Tìm m để phương trình x^4-2x^2+3-10có 4 nghiệm mà điểm biễu diễn của chúng trên trục hoành cách đều nhau.4. Cho hệ phương trình hept{begin{cases}mx+y2mx+mym+1end{cases}}Tìm giá trị nguyên âm của m để hệ phương trình trên có nghiệm (x;y) nguyên
Đọc tiếp
1. Số nghiệm của hệ phương trình \(\hept{\begin{cases}x^3+2xy^2+12=0\\x^28y^2=12\end{cases}}\)
2. Giá trị nghuyên nhỏ nhất của m để phương trình \(x^3+mx=0\)có 3 nghiệm riêng biệt.
3. Tìm m để phương trình \(x^4-2x^2+3-1=0\)có 4 nghiệm mà điểm biễu diễn của chúng trên trục hoành cách đều nhau.
4. Cho hệ phương trình \(\hept{\begin{cases}mx+y=2m\\x+my=m+1\end{cases}}\)
Tìm giá trị nguyên âm của m để hệ phương trình trên có nghiệm (x;y) nguyên
4.
(1) => y=2m-mx thay vào (2) ta được x+m(2m-mx)=m+1
<=> x-m2x=-2m2+m+1
<=> x(1-m)(1+m)=-(m-1)(1+2m)
với m=-1 thì pt vô nghiệm
với m=1 thì pt vô số nghiệm => có nghiệm nguyên => chọn
với m\(\ne\pm\) 1 thì x=\(\frac{-2m-1}{m+1}\)=\(-2+\frac{1}{m+1}\)
=> y=2m-mx=xm-m(-2+\(\frac{1}{m+1}\)) =2m+2m-\(\frac{m}{m+1}\)=4m-1+\(\frac{1}{m+1}\)
để x y nguyên thì \(\frac{1}{m+1}\)nguyên ( do m nguyên)
=> m+1\(\in\)Ư(1)={1;-1}
=> m\(\in\){0;-2} mà m nguyên âm nên m=-2
vậy m=-2 thì ...
P/s hình như 1 2 3 sai đề
Đúng 0
Bình luận (0)
cho hệ phương trình :{x+my=3 và mx+4y=7
1,giải hệ phương trình khi m=3
2,tìm m để hệ có nghiệm{x>1 và y>0
1/ khi m=3 ta có
x+3y=3
3x+4y=7
<=>x=3-3y
3(3-3y)+4y=7
<=>x=3-3y
3y+4y=7
<=>x=3-3y
7y=7
==>y=1
<=>x=3-3y
=>x=3-3.1
=>x=3-3
==>x=0
vây x=0 ; y=1
Đúng 0
Bình luận (0)
Cho hệ phương trình mx+2y=m+2 (2m-1)x+(m + 1)y = 2(m + 1)a) Giải hệ phương trình với m = 3 ? b) Tìm giá trị của m để hệ phương trình có nghiệm duy nhất , vô số nhiệm
a: \(\left\{{}\begin{matrix}mx+2y=m+2\\\left(2m-1\right)x+\left(m+1\right)y=2\left(m+1\right)\end{matrix}\right.\)
Khi m=3 thì hệ sẽ là:
3x+2y=5 và 5x+4y=8
=>x=2 và y=-1/2
b: Hệ có nghiệm duy nhất thì \(\dfrac{m}{2m-1}< >\dfrac{2}{m+1}\)
=>m^2+m<>4m-2
=>m^2-3m+2<>0
=>m<>1 và m<>2
hệ có vô số nghiệm thì \(\dfrac{m}{2m-1}=\dfrac{2}{m+1}=\dfrac{2}{2\left(m+1\right)}=\dfrac{1}{m+1}\)
=>m/2m-1=2/m+1 và 2/m+1=1/m+1(vô lý)
=>Ko có m thỏa mãn
Để hệ vô nghiệm thì m/2m-1=2/m+1<>1/m+1
=>m=2 hoặc m=1
Đúng 1
Bình luận (0)
cho hệ phương trình {x+2y=2 , mx-y=m (m là tham số) a) giải hệ phương trình khi m=2 b) tìm m để hệ phương trình nhận cặp (x,y)=(2,-1) làm nghiệm
a, tại m=2 thì hệ tương đương với\(\hept{\begin{cases}x+2y=2\\2x-y=2\end{cases}\Leftrightarrow\hept{\begin{cases}x+2y=2\\4x-2y=4\end{cases}\Leftrightarrow\hept{\begin{cases}x+2y=2\\5x=6\end{cases}\Leftrightarrow\hept{\begin{cases}x=\frac{6}{5}\\y=\frac{2}{5}\end{cases}}}} }\)
b, do thay (x,y)=(2,-1) vào phương trình x+2y=2 không thỏa mãn nên hệ phương trình không nhận cặp (x,y)=(2,-1) là nghiệm
cho hệ phương trình: mx + y=2m +2 x+my=11/ khi m= -3 tìm hệ phương trình2/ tìm m để hệ phương trình có: 1 nghiệm duy nhất, vô nghiệm, vô số nghiệm3/ giải hệ theo m
Xem chi tiết
1: mx+y=2m+2 và x+my=11
Khi m=-3 thì hệ sẽ là:
-3x+y=-6+2=-4 và x-3y=11
=>-3x+y=-4 và 3x-9y=33
=>-8y=29 và 3x-y=4
=>y=-29/8 và 3x=y+4=3/8
=>x=1/8 và y=-29/8
2: Để hệ có 1 nghiệm duy nhất thì \(\dfrac{m}{1}< >\dfrac{1}{m}\)
=>m^2<>1
=>m<>1 và m<>-1
Để hệ vô số nghiệm thì \(\dfrac{m}{1}=\dfrac{1}{m}=\dfrac{2m+2}{11}\)
=>(m=1 hoặc m=-1) và (11m=2m+2)
=>\(m\in\varnothing\)
Để hệ vô nghiệm thì m/1=1/m<>(2m+2)/11
=>m=1 hoặc m=-1
Đúng 1
Bình luận (1)
Cho hệ phương trình: \(\left\{{}\begin{matrix}x+my=3m\\mx-y=m^2-2\end{matrix}\right.\)
Tìm m để hệ phương trình có nghiệm (x,y) thỏa mãn x2 - 2x - y > 0
Hệ \(\Leftrightarrow\left\{{}\begin{matrix}x=3m-my\\mx-y=m^2-2\end{matrix}\right.\)
\(\Rightarrow m\left(3m-my\right)-y=m^2-2\)
\(\Leftrightarrow2m^2+2=y\left(1+m^2\right)\)
\(\Leftrightarrow y=\dfrac{2m^2+2}{1+m^2}=2\)
\(\Rightarrow x=3m-2m=m\)
Có \(x^2-2x-y>0\Leftrightarrow m^2-2m-2>0\)
\(\Leftrightarrow\left(m-1-\sqrt{3}\right)\left(m-1+\sqrt{3}\right)>0\)
\(\Leftrightarrow\left[{}\begin{matrix}m>1+\sqrt{3}\\m< 1-\sqrt{3}\end{matrix}\right.\)
Vậy...
Đúng 2
Bình luận (8)
Cho hệ phương trình
m
x
+
(
m
+
2
)
y
5
x
+
m
y...
Đọc tiếp
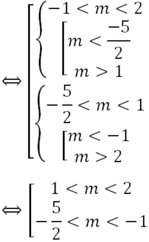
Cho hệ phương trình m x + ( m + 2 ) y = 5 x + m y = 2 m + 3 Giá trị cần tìm của tham số m để hệ phương trình có nghiệm y< 0 là :
![]()
![]()
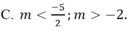
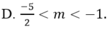
1/Cho hệ phương trình \(\hept{\begin{cases}mx+y=2m\\x+my=m+1\end{cases}}\) tìm các giá trị nguyên âm của m để hệ phương trình trên có nghiệm (x;y) nguyên
2/ Tìm giá trị nguyên nhỏ nhất của m để phương trình \(x^3-mx=0\) có 3 nghiệm phân biệt