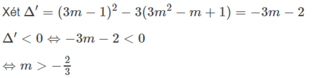với giá trị nào của m thì phương trình (m-1)x - m + 2 = 0 vô nghiệm

Những câu hỏi liên quan
Cho phương trình 3 x 2 + 2 ( 3 m - 1 ) x + 3 m 2 - m + 1 = 0 . Với giá trị nào của m thì phương trình vô nghiệm?
Cho phương trình 2x2-(4m+3)x+2m2+1=0
A) Giải phương trình m=1?
B) Với giá trị nào của m thì phương trình có nghiệm?
C) Với giá trị nào của m thì phương trình vô nghiệm?
A) Giải phương trình m=1?
B) Với giá trị nào của m thì phương trình có nghiệm?
C) Với giá trị nào của m thì phương trình vô nghiệm?
Cho phương trình (ẩn x) x2 – 2(m – 1)x + m2 = 0
Với giá trị nào của m thì phương trình có hai nghiệm phân biệt? Có nghiệm kép? Vô nghiệm.
Phương trình (1):
+ Vô nghiệm ⇔ Δ’ < 0 ⇔ 1 – 2m < 0 ⇔ 2m > 1 ⇔ m > 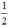
+ Có nghiệm kép ⇔ Δ’ = 0 ⇔ 1 – 2m = 0 ⇔ m = 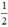
+ Có hai nghiệm phân biệt ⇔ Δ’ > 0 ⇔ 1 – 2m > 0 ⇔ 2m < 1 ⇔ m < 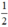
Vậy: Phương trình (1) có hai nghiệm phân biệt khi m < 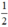 ; có nghiệm kép khi m =
; có nghiệm kép khi m = 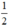 và vô nghiệm khi m >
và vô nghiệm khi m > 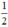
Đúng 0
Bình luận (0)
Cho phương trình (ẩn x) x 2 – 2 ( m – 1 ) x + m 2 = 0
a) Tính Δ'.
b) Với giá trị nào của m thì phương trình có hai nghiệm phân biệt? Có nghiệm kép? Vô nghiệm.
a) Phương trình x 2 – 2 ( m – 1 ) x + m 2 = 0 (1)
Có a = 1; b’ = -(m – 1); c = m 2
b) Phương trình (1):
+ Vô nghiệm ⇔ Δ’ < 0 ⇔ 1 – 2m < 0 ⇔ 2m > 1 ⇔ m > 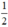
+ Có nghiệm kép ⇔ Δ’ = 0 ⇔ 1 – 2m = 0 ⇔ m = 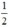
+ Có hai nghiệm phân biệt ⇔ Δ’ > 0 ⇔ 1 – 2m > 0 ⇔ 2m < 1 ⇔ m < 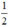
Vậy: Phương trình (1) có hai nghiệm phân biệt khi m < 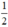 ; có nghiệm kép khi m =
; có nghiệm kép khi m = 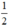 và vô nghiệm khi m >
và vô nghiệm khi m > 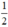
Đúng 0
Bình luận (0)
Cho hệ pt: \(\left\{{}\begin{matrix}3x-y=2\\9x-my=m\end{matrix}\right.\)
1. Với giá trị nào của m thì hệ phương trình vô nghiệm
2. Với giá trị nào của m thì hệ phương trình có vô số nghiệm?
3. Với giá trị nào của m thì hệ phương trình có nghiệm duy nhất
4. Tìm m để hệ có nghiệm duy nhất x> 0; y<0
Cho phương trình : ( 2m — 3 ) x + ( x − 3 ) 4m + 2mx = 0
a ) Với giá trị nào của m thì phương trình trên là phương trình bậc nhất ? Tìm nghiệm của nó . b ) Với giá trị nào của m thì phương trình vô nghiệm ? c ) Với giá trị nào của m thì phương trình vô số nghiệm ?
Giúp mình với, mình cần gấp
a) Để phương trình trên là phương trình bậc nhất thì: m≠\(\dfrac{3}{8}\)
c) Để phương trình vô nghiệm thì: m=0
d) Để phương trình vô số nghiệm thì m=\(\dfrac{3}{8}\)
Đúng 1
Bình luận (0)
a/ \(\left(2m-3\right)x+\left(x-3\right)4m+2mx=0\)
\(\Leftrightarrow\left(8m-3\right)x-12m=0\)
Để phương trình là hàm số bậc 1 :
\(8m-3\ne0\Leftrightarrow m\ne\dfrac{3}{8}\)
b/ Phương trình vô nghiệm :
\(\Leftrightarrow\left\{{}\begin{matrix}8m-3=0\\12m\ne0\end{matrix}\right.\)
c/ Phương trình vô số nghiệm khi :
\(\Leftrightarrow\left\{{}\begin{matrix}8m-3=0\\12m=0\end{matrix}\right.\)
Đúng 0
Bình luận (0)
(2m-3)x+(x-3)4m+2mx=0
=>(2m-3)x+4mx-12m+2mx=0
=>x(2m-3+4m+2m)-12m=0
=>-3x-12m=0
a: Để phương trình là phương trình bậc nhất thì 2m-3-4m+2m<>0
hay \(m\in R\)
b: Để phương trình vô nghiệm thì \(m\in\varnothing\)
Đúng 0
Bình luận (0)
cho hệ phương trình mx -y =2m 4x - my=6+m Với giá trị nào của m thì hệ phương trình có duy nhất một nghiệm Với giá trị nào của m thì hệ phương trình có vô số nghiệm Với giá trị nào của m thì hệ phương trình vô nghiệm
a: Để hệ có duy nhất 1 nghiệm thì \(\dfrac{m}{4}< >\dfrac{-1}{-m}=\dfrac{1}{m}\)
=>m^2<>4
=>m<>2 và m<>-2
b: Để hệ có vô số nghiệm thì \(\dfrac{m}{4}=\dfrac{-1}{-m}=\dfrac{2m}{m+6}=\dfrac{1}{m}\)
=>m^2=4 và 2m^2=m+6
=>m=2
c: Để hệ vô nghiệm thì m/4=1/m<>2m/m+6
=>m=-2
Đúng 0
Bình luận (0)
Với giá trị nào của tham số m thì phương trình \(\left(m^2-1\right)x+m^2-2m-3=0\) vô nghiệm ?
A. \(m=1\) B. \(m=-1\) C. \(m=-2\) D. \(m=-3\)
\(\Leftrightarrow\left\{{}\begin{matrix}m^2-1=0\\m^2-2m-3\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=\pm1\\m\ne-1;m\ne3\end{matrix}\right.\Leftrightarrow m=1\)
Chọn A
Đúng 2
Bình luận (0)