CÂU 11: Cho tứ giác ABCD, AC=BD, AC thuộc BD ; Gọi M, N ,P, Q lần lượt là trung điểm của AB, BC, CD, DA. Khi đó MNPQ là hình gì ? Lời giải ?

Những câu hỏi liên quan
cho tứ giác ABCD . gọi O là giao điểm của hai đường chéo AC và BD . Gọi chu vi tứ giác ABCD là PABCD Chứng minh
a)AC+BD>\(\dfrac{P_{ABCD}}{2}\)
b)Nếu AC<\(\dfrac{P_{ABCD}}{2}\) thì AC+BD<PABCD
Câu 17:. Chọn câu đúng:A. Tứ giác ABCD là hình chữ nhật khi có và . B. Tứ giác ABCD là hình chữ nhật khi có và . C. Tứ giác ABCD là hình chữ nhật khi có ABCD; ADBC; ACBD. D. Tứ giác ABCD là hình chữ nhật khi có ABCD; ABBC và ACBD.
Đọc tiếp
Câu 17:. Chọn câu đúng:
A. Tứ giác ABCD là hình chữ nhật khi có và
.
B. Tứ giác ABCD là hình chữ nhật khi có và
.
C. Tứ giác ABCD là hình chữ nhật khi có AB=CD; AD=BC; AC=BD.
D. Tứ giác ABCD là hình chữ nhật khi có AB=CD; AB=BC và AC=BD.
cho tứ giác ABCD . gọi O là giao điểm của hai đường chéo AC và BD . gọi chu vi của tứ giác ABCD là PABCD . chứng minh
a) AC+BD>\(\dfrac{P_{ABCD}}{2}\)
b) Nếu AC<\(\dfrac{P_{ABCD}}{2}\) thì AC+BD<PABCD
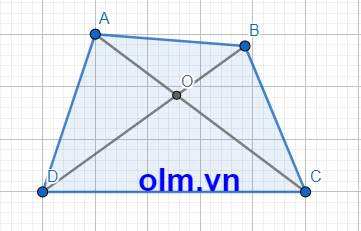
a, Xét \(\Delta\) AOB có: AO+OB > AB (trong tam giác tổng hai cạnh luôn lớn hơn cạnh còn lại)
Tương tự ta có: OC + OD > DC
OA + OD > AD
OB + OC > BC
Cộng vế với vế ta có:
OA+OB+OC+OD+OA+OD+OB+OC > AB +DC+AD+BC
(OA+OC)\(\times\)2 + (OB + OD)\(\times\)2 > PABCD
AC \(\times\) 2 + BD \(\times\) 2 > PABCD
AC + BD > \(\dfrac{P_{ABCD}}{2}\) (đpcm)
b, Xét \(\Delta\) ABD có: AB + AD > BD (trong tam giác tổng hai cạnh bao giờ cũng lớn hơn cạnh còn lại)
Tương tự ta có: AD + DC > AC
DC + CB > DB
CB + AB > AC
Cộng vế với vế ta có:
AB+AD+AD+DC+DC+CB+CB+AB >BD+ AC+DB+AC
2AB+2BC+2CD+2AD> 2AC + 2BD
2(AB + BC + CD + AD) > 2(AC + BD)
AB + BC + CD + AD > AC + BD
PABCD > AC + BD (đpcm)
Đúng 1
Bình luận (0)
Cho tứ giác ABCD có AC = BD và AC vuông góc BD. khi đó : A. Tứ giác ABCD là hình vuông B. Tứ giác ABCD là hình bình hành C. Tứ giác ABCD là hình thoi D. ABCD là tứ giác bất kì
Cho tứ giác ABCD có góc A= Góc C= 90 độ
a) Chứng minh bốn đỉnh của tứ giác cùng thuộc 1 đường tròn
b) Chứng minh AC\(\le\)BD
c) Nếu AC=BD thì tứ giác ABCD là hình gì ?
Cho tứ giác ABCD có O là giao điểm hai đường chéo AC và BD, hỏi nếu AC=BD thì tứ giác ABCD là hình gì ?
Tứ giác ABCD là một hình vuông.
Đúng 0
Bình luận (0)
Cho tứ giác ABCD có AC = BD và AC ⊥ BD. Khi đó:
A. Tứ giác ABCD là hình vuông.
B. Tứ giác ABCD là hình bình hành.
C. Tứ giác ABCD là hình thoi.
D. ABCD là tứ giác bất kỳ.
Cho hình tứ giác ABCD. Kẻ BF// CD , CG//AB (G thuộc BD , F thuộc AC). CM FG//AD
Cho tứ giác ABCD có AC vuông góc với BD, AC=8cm, BD=5cm. Hãy tính diện tích tứ giác đó.
tự vẽ hình nha bạn
gọi giao điểm của AC và BD la O
Ta có BO + DO = BD
mà diện h của ΔACD là: \(\frac{AC\cdot DO}{2}=\frac{8\cdot DO}{2}\)
diện h của ΔACB là: \(\frac{AC\cdot BO}{2}=\frac{8\cdot BO}{2}\)
nên diện h của tứ gái ABCD là \(\frac{8\cdot DO}{2}+\frac{8\cdot BO}{2}=\frac{8\cdot DO+8\cdot BO}{2}=\frac{8\left(DO+BO\right)}{2}=4\cdot5=20\left(cm\right)\)
Đúng 0
Bình luận (0)




















