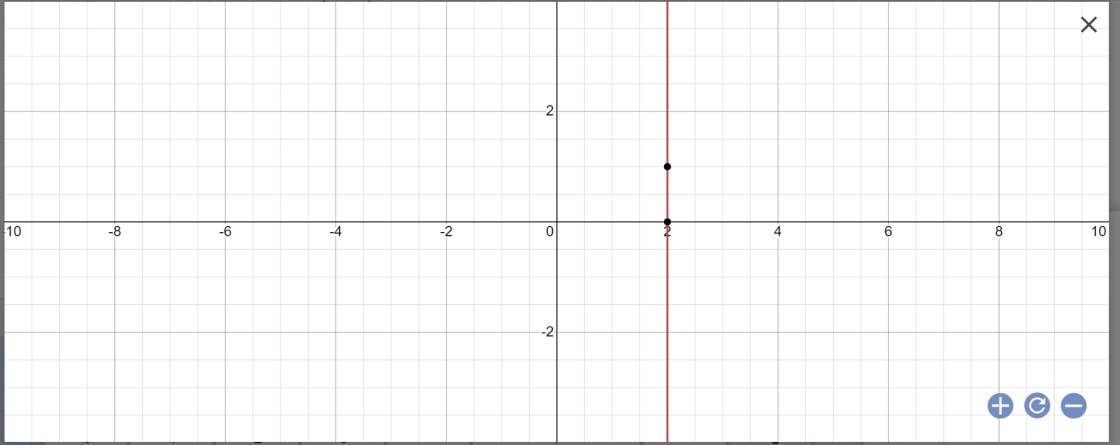
Tìm nghiệm tổng quát sau đó suy ra 3 nghiệm cụ thể của các phương trình sau :
a) 2x + 3y = 5
b) x - 2y = 4
viết công thức nghiệm tổng quát và biểu diễn tập nghiệm của phương trình sau trên mặt phẳng tọa độ :
a)2x-3y=5
b)4x+0y=12
c)0x-3y=6
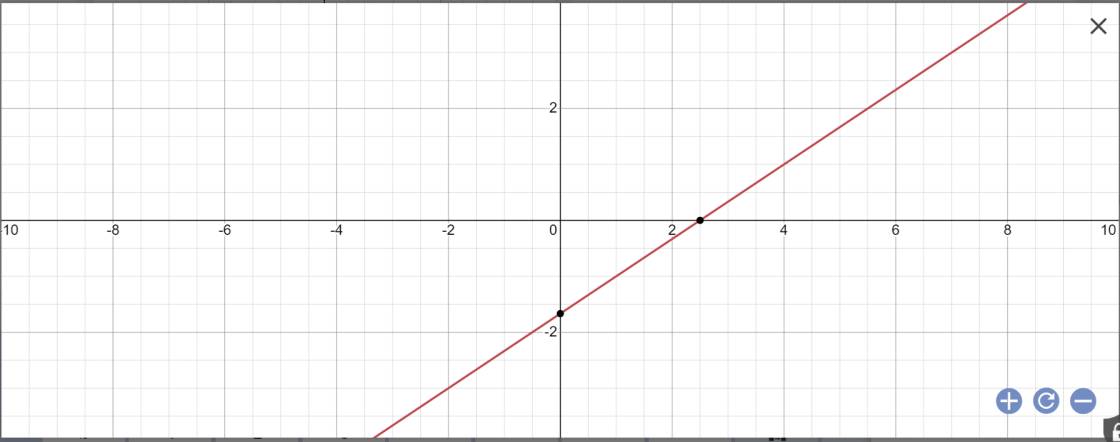
a: 2x-3y=5
=>3y=2x-5
=>\(y=\dfrac{2}{3}x-\dfrac{5}{3}\)
Vậy: Công thức nghiệm tổng quát là \(\left\{{}\begin{matrix}x\in R\\y=\dfrac{2}{3}x-\dfrac{5}{3}\end{matrix}\right.\)
Biểu diễn tập nghiệm:
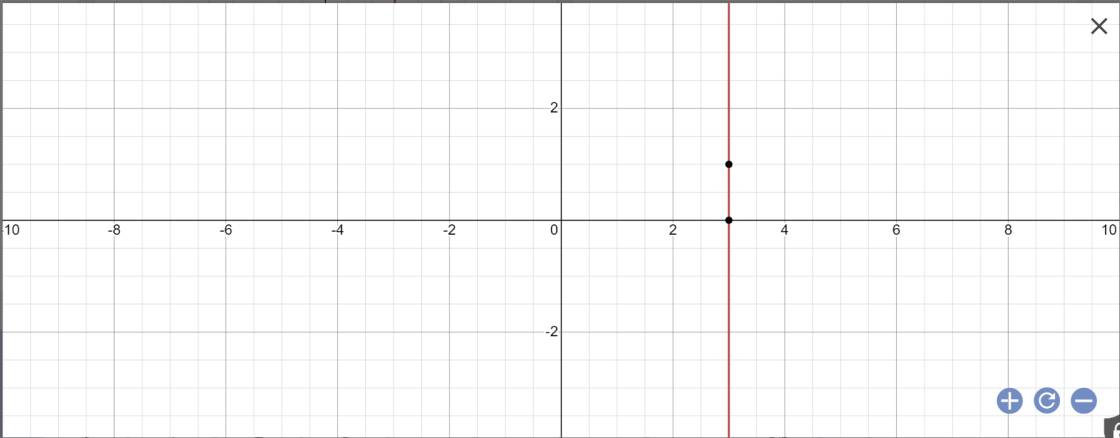
b: 4x+0y=12
=>4x=12
=>x=3
Vậy: Công thức nghiệm tổng quát là \(\left\{{}\begin{matrix}x=3\\y\in R\end{matrix}\right.\)
Biểu diễn tập nghiệm:
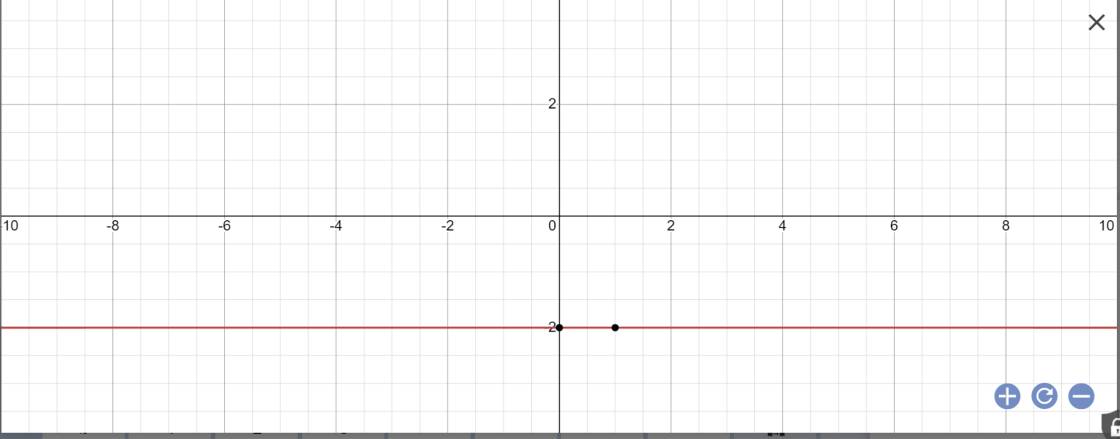
c: 0x-3y=6
=>-3y=6
=>y=-2
Vậy: Công thức nghiệm tổng quát là \(\left\{{}\begin{matrix}x\in R\\y=-2\end{matrix}\right.\)
Biểu diễn tập nghiệm:
Với mỗi phương trình sau, tìm nghiệm tổng quát của phương trình và vẽ hai đường thẳng biểu diễn tập nghiệm của hai phương trình đó trên cùng một hệ toạ độ. Xác định toạ độ giao điểm của hai đường thẳng
2x + y = 3
x-2y = 4
bạn ưi, cho gửi lại tại vì hơi bị lộn kiến thức :)
tìm nghiệm tổng quát:
2x+y=4⇔x=2-1/2y hay y=4-2x
⇔y∈R ⇔ x∈R
x=2-1/2y y=4-2x
3x-2y=4⇔x=4/3+2/3yhay y=3/2x-2
⇔y∈R hay ⇔x∈R
x=4/3+2/3y y=3/2x-2
còn biểu diễn 2 cái đấy trên trục tọa độ thì mik làm r
Với mỗi phương trình sau, tìm nghiệm tổng quát của phương trình và vẽ đường thẳng biểu diễn tập nghiệm của nó:
a) 3x – y = 2; b) x + 5y = 3;
c) 4x – 3y = -1; d) x + 5y = 0 ;
e) 4x + 0y = -2 ; f) 0x + 2y = 5.
a) 3x – y = 2 (1)
⇔ y = 3x – 2.
Vậy phương trình có nghiệm tổng quát là (x; 3x – 2) (x ∈ R).
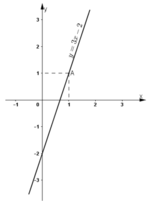
Đường thẳng biểu diễn tập nghiệm của phương trình (1) là đường thẳng y = 3x – 2 (Hình vẽ).
+ Tại x = 2/3 thì y = 0 ⇒ đường thẳng y = 3x – 2 đi qua điểm (2/3 ; 0).
+ Tại x = 0 thì y = -2 ⇒ đường thẳng y = 3x – 2 đi qua điểm (0; -2).
Vậy đường thẳng y = 3x – 2 là đường thẳng đi qua điểm (2/3 ; 0) và (0; -2).
b) x + 5y = 3 (2)
⇔ x = 3 – 5y
Vậy phương trình có nghiệm tổng quát là (3 – 5y; y) (y ∈ R).
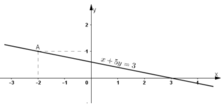
Đường thẳng biểu diễn tập nghiệm của (2) là đường thẳng x + 5y = 3.
+ Tại y = 0 thì x = 3 ⇒ Đường thẳng đi qua điểm (3; 0).
+ Tại x = 0 thì y=3/5 ⇒ Đường thẳng đi qua điểm (0; 3/5).
Vậy đường thẳng x + 5y = 3 là đường thẳng đi qua hai điểm (3; 0) và (0; 3/5).
c) 4x – 3y = -1
⇔ 3y = 4x + 1
⇔ 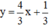
Vậy phương trình có nghiệm tổng quát là (x;4/3x+1/3)(x ∈ R).
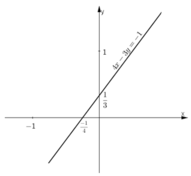
Đường thẳng biểu diễn tập nghiệm phương trình là đường thẳng 4x – 3y = -1.
+ Tại x = 0 thì y = 1/3
Đường thẳng đi qua điểm (0;1/3) .
+ Tại y = 0 thì x = -1/4
Đường thẳng đi qua điểm (-1/4;0) .
Vậy đường thẳng 4x – 3y = -1 đi qua (0;1/3) và (-1/4;0).
d) x + 5y = 0
⇔ x = -5y.
Vậy nghiệm tổng quát của phương trình là (-5y; y) (y ∈ R).
Đường thẳng biểu diễn nghiệm của phương trình là đường thẳng x + 5y = 0.
+ Tại x = 0 thì y = 0 ⇒ Đường thẳng đi qua gốc tọa độ.
+ Tại x = 5 thì y = -1 ⇒ Đường thẳng đi qua điểm (5; -1).
Vậy đường thẳng x + 5y = 0 đi qua gốc tọa độ và điểm (5; -1).
e) 4x + 0y = -2
⇔ 4x = -2 ⇔ 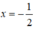
Phương trình có nghiệm tổng quát (-0,5; y)(y ∈ R).
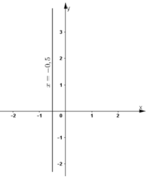
Đường thẳng biểu diễn tập nghiệm là đường thẳng x = -0,5 đi qua điểm (-0,5; 0) và song song với trục tung.
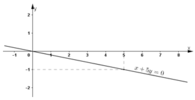
f) 0x + 2y = 5
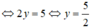
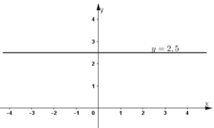
Phương trình có nghiệm tổng quát (x; 2,5) (x ∈ R).
Đường thẳng biểu diễn tập nghiệm là đường thẳng y = 2,5 đi qua điểm (0; 2,5) và song song với trục hoành.
Viết công thức nghiệm tổng quát của phương trình
a. 3x + 2y = 5
b. 5x - 3y = 6
c. 4x - 3y = 5
d. 3x + 2y = 7
a) \(y=\dfrac{5-3x}{2}\)
b) \(y=\dfrac{5x-6}{3}\)
c) \(y=\dfrac{4x-5}{3}\)
d) \(y=\dfrac{7-3x}{2}\)
a. 3x + 2y = 5
<=> 2(1,5x + y) = 5
<=> 1,5x + y = 2,5
<=> \(\left[{}\begin{matrix}x=\dfrac{2,5-y}{1,5}\\y=2,5-1,5x\end{matrix}\right.\)
Viết nghiệm tổng quát và vẽ đường thẳng biểu diễn tập nghiệm của mỗi phương trình sau: 2x + 3y = 5
Cho hai phương trình 2x + y = 4 và 3x + 2y = 5.
a) Tìm nghiệm tổng quát của mỗi phương trình trên.
b) Vẽ các đường thẳng biểu diễn tập nghiệm của hai phương trình trong cùng một hệ trục tọa độ, rồi xác định nghiệm chung của chúng.
a) + Xét phương trình 2x + y = 4 (1) ⇔ y = -2x + 4
Vậy phương trình (1) có nghiệm tổng quát là (x ; -2x + 4) (x ∈ R).
+ Xét phương trình 3x + 2y = 5 (2) ⇔ 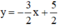
Vậy phương trình (2) có nghiệm tổng quát là : 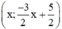 (x ∈ R).
(x ∈ R).
b) Đường thẳng biểu diễn tập nghiệm của phương trình (1) là đường thẳng (d) : y = -2x + 4.
Chọn x = 0 ⇒ y = 4
Chọn y = 0 ⇒ x = 2.
⇒ (d) đi qua hai điểm (0; 4) và (2; 0).
Đường thẳng biểu diễn tập nghiệm của phương trình (2) là đường thẳng (d’) : 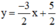
Chọn x = 0 ⇒ y = 2,5.
Chọn y = 0 ⇒ 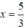
⇒ (d’) đi qua hai điểm (0; 2,5) và 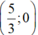
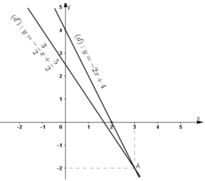
Hai đường thẳng cắt nhau tại A(3; -2).
Vậy (3; -2) là nghiệm chung của hai phương trình (1) và (2).
Viết nghiệm tổng quát và vẽ đường thẳng biểu diễn tập nghiệm của mỗi phương trình sau: x + 2y = 4
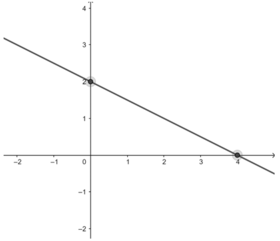
x + 2y = 4
Chọn x = 0 ⇒ y = 2. Đường thẳng đi qua điểm (0; 2)
Chọn y = 0 ⇒ x = 4 . Đường thẳng đi qua điểm (4; 0)
Vậy đường thẳng x + 2y = 4 đi qua hai điểm (0; 2) và (4; 0)
Với mỗi phương trình sau, tìm nghiệm tổng quát của phương trình và vẽ đường thẳng biểu diễn tập nghiệm của nó:
4x – 3y = -1
4x – 3y = -1
⇔ 3y = 4x + 1
⇔ 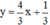
Vậy phương trình có nghiệm tổng quát là 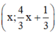 (x ∈ R).
(x ∈ R).
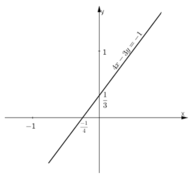
Đường thẳng biểu diễn tập nghiệm phương trình là đường thẳng 4x – 3y = -1.
+ Tại x = 0 thì y = 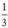
Đường thẳng đi qua điểm 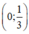 .
.
+ Tại y = 0 thì x = 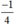
Đường thẳng đi qua điểm 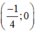 .
.
Vậy đường thẳng 4x – 3y = -1 đi qua  và
và 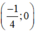 .
.
1 tìm nghiệm tổng quát và vẽ đô thị biểu diễn tập nghiệm của pt
A) x-2y = 5 c) 0x+3y = 4
B) 3y-x = 2 d) 2x+0y = 4
a: x-2y=5
=>2y=x-5
=>y=1/2x-5
Nghiệm tổng quát là: \(\left\{{}\begin{matrix}x\in R\\y=\dfrac{1}{2}x-5\end{matrix}\right.\)
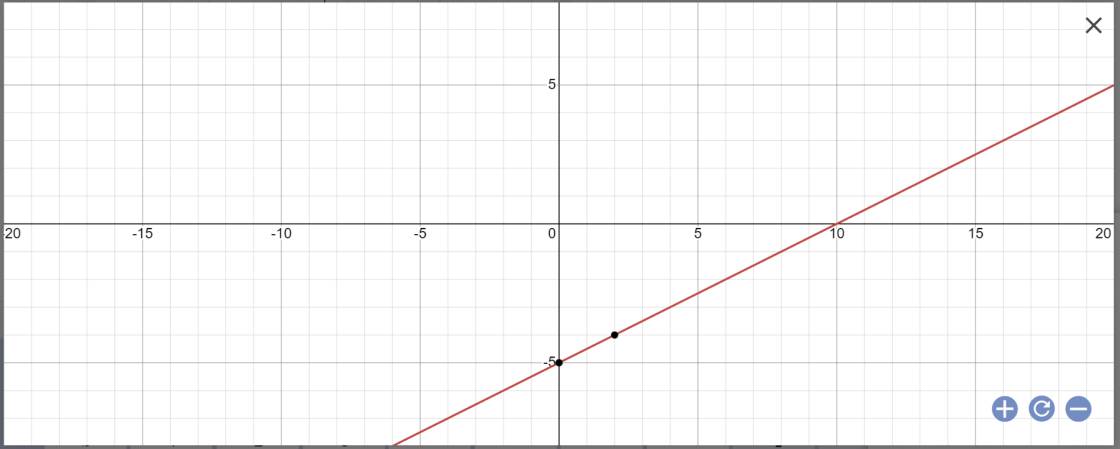
b: 3y-x=2
=>3y=x+2
=>y=1/3x+2
Nghiệm tổng quát là \(\left\{{}\begin{matrix}x\in R\\y=\dfrac{1}{3}x+2\end{matrix}\right.\)
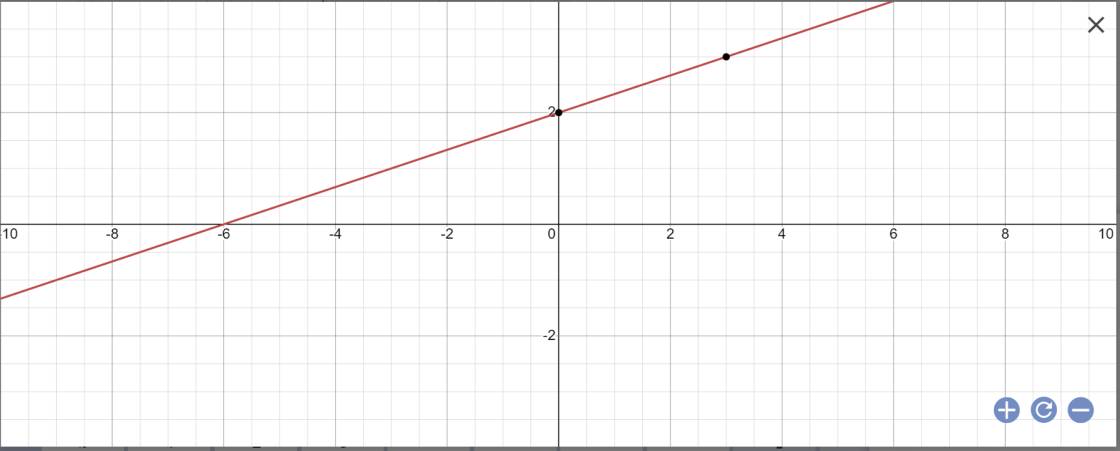
c: 0x+3y=4
=>3y=4
=>y=4/3
=>Nghiệm tổng quát là \(\left\{{}\begin{matrix}x\in R\\y=\dfrac{4}{3}\end{matrix}\right.\)
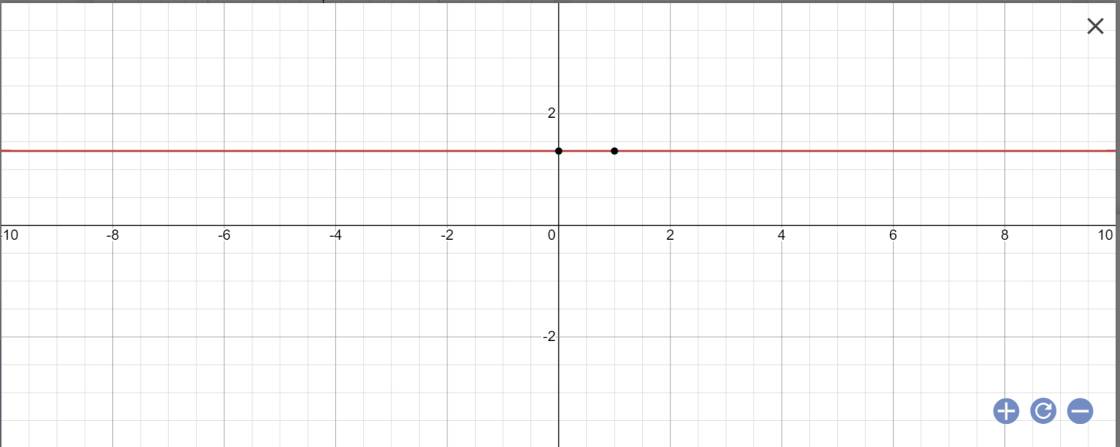
d: 2x+0y=4
=>2x=4
=>x=2
=>Nghiệm tổng quát là \(\left\{{}\begin{matrix}x=2\\y\in R\end{matrix}\right.\)