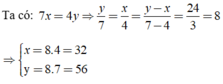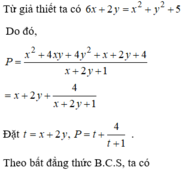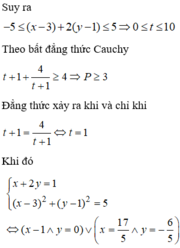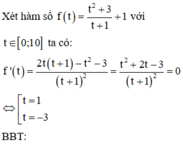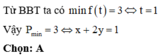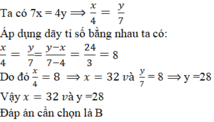Cho 7x=4y và y-x=24, giá trị của x là ...

Những câu hỏi liên quan
Cho 7x=4y và y-x=24. Tính giá trị của x
+ 7x = 4y
\(\Leftrightarrow y=\dfrac{7x}{4}\)
+ y - x = 24
\(\Leftrightarrow y=24+x\)
\(\Rightarrow24+x=\dfrac{7x}{4}\)
\(\Leftrightarrow x=32\)
Đúng 1
Bình luận (0)
\(7x=4y\)
⇒ \(\dfrac{x}{4}=\dfrac{y}{7}\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\dfrac{x}{4}=\dfrac{y}{7}=\dfrac{y-x}{7-4}=\dfrac{24}{3}=8\)
⇒ \(\left\{{}\begin{matrix}x=8.4=32\\y=8.7=56\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Cho 7x = 4y và y - x = 24. Tìm giá trị x, y?
A. y = 4; x = 7
B. x = 32; y = 56
C. x = 56; y = 32
D. x = 4; y = 7
Cho x, y là các số thực thỏa mãn
(
x
−
3
)
2
+
(
y
−
1
)
2
5
. Giá trị nhỏ nhất của biểu thức
P
3
y
2
+...
Đọc tiếp
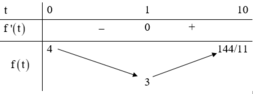
Cho x, y là các số thực thỏa mãn ( x − 3 ) 2 + ( y − 1 ) 2 = 5 . Giá trị nhỏ nhất của biểu thức P = 3 y 2 + 4 x y + 7 x + 4 y − 1 x + 2 y + 1 là
A. 2 3 .
B. 3 .
C. 114 11 .
D. 3
Toán lớp 0 ????? \(\text{ 🤔 }\text{ 🤔 }\text{ 🤔 }\text{ 😅 }\text{ 😅 }\text{ 😅 }\)
Cho x, y là các số thực thỏa mãn
x
−
3
2
+
y
−
1
2
5
. Tìm giá trị nhỏ nhất của biểu thức
P
3
y
2
+
4
x...
Đọc tiếp
Cho x, y là các số thực thỏa mãn x − 3 2 + y − 1 2 = 5 . Tìm giá trị nhỏ nhất của biểu thức P = 3 y 2 + 4 x y + 7 x + 4 y − 1 x + 2 y + 1
A. 3
B. 3
C. 114 11
D. 2 3
Cho 7x = 4y và y-x = 24. Tìm x;y
A. y = 4 ; x = 7
B. x = 32 ; y = 56
C. x = 56 ; y = 32
D. x = 4 ; y = 7
Cho 7x = 4y và y-x= 24. tính x và y
theo t/c đề bài ta có: x/4=y/7 và y-x=24
theo t/c dãy tỉ số bằng nhau ta có: x/4=y/7=y-x/7-4=6
=)x/4=6=)x=6.4=24
=)y/7=6=)y=6.7=42
vậy x=24 và y=42
chú ý là dấu chấm là dấu nhân
Đúng 0
Bình luận (0)
\(7x=4y\) va y-x=24
\(7x=4y\Rightarrow\frac{x}{4}=\frac{y}{7}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{x}{4}=\frac{y}{7}=\frac{y-x}{7-4}=\frac{24}{3}=8\)
Suy ra : \(\frac{x}{4}=8\Rightarrow x=8.4=32\)
\(\frac{y}{7}=8\Rightarrow y=8.7=56\)
Đúng 2
Bình luận (0)
cho 7x=4y và y-x=24.tìm x,y
Theo bài ra ta có :
\(7x=4y\Rightarrow\frac{x}{4}=\frac{y}{7}\)
Áp dụng tính chất của dãy tỉ số bằng nhau , ta có :
\(\frac{x}{4}=\frac{y}{7}=\frac{y-x}{7-4}=\frac{24}{3}=8\)
\(\frac{x}{4}=8\Rightarrow x=32\)
\(\frac{y}{7}=8\Rightarrow y=56\)
Vậy x = 32 ; y = 56
Đúng 0
Bình luận (0)
Ta có:
\(7x=4y\)và y-x=24
=>\(\frac{x}{4}=\frac{y}{7}\)và y-x=24
=>\(\frac{y}{7}=\frac{x}{4}\)và y-x=24
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{y}{7}=\frac{x}{4}=\frac{y-x}{7-4}=\frac{24}{3}=8\)
\(=>\hept{\begin{cases}\frac{y}{7}=8=>y=8.7=56\\\frac{x}{4}=8=>x=8.4=32\end{cases}}\)
Vậy \(\hept{\begin{cases}y=56\\x=32\end{cases}}\)
Đúng 0
Bình luận (0)
Rút gọn rồi tính giá trị của các biểu thức sau:
1) A=2x(x-y)-y(y-2x) với x = -2/3 ; y=-1/3
2)B=5x(x-4y)-4y(y-5x) với x=-1/5 ;y=-1/2
3)C=x.(x^2-y^2)-x^2(x+y)+y(x^2-x) tại x=1/2 và y=-100
4)D=5x(x^2y-3) -x^2y(7x-5x)-7x^2 tại x=-5 và y=-1
\(1)A=2x\left(x-y\right)-y\left(y-2x\right)\)
\(=2x^2-2xy-y^2+2xy\)
\(=2x^2-y^2=2.\left(-\dfrac{2}{3}\right)^2-\left(-\dfrac{1}{3}\right)^2\)
\(=\dfrac{8}{9}-\dfrac{1}{9}=\dfrac{7}{9}\)
\(2)B=5x\left(x-4y\right)-4y\left(y-5x\right)\)
\(=5x^2-20xy-4y^2+20xy\)
\(=5x^2-4y^2=5.\left(-\dfrac{1}{5}\right)^2-4.\left(-\dfrac{1}{2}\right)^2=\dfrac{1}{5}-1=-\dfrac{4}{5}\)
\(3)C=\text{x.(x^2-y^2)-x^2(x+y)+y(x^2-x)}\)
\(=x^3-xy^2-x^3-x^2y+x^2y-xy\)
\(=-xy\left(x+1\right)\)
Đúng 1
Bình luận (0)
\(=\dfrac{1}{2}.100\left(100+1\right)=50.101=5050\)
Đúng 0
Bình luận (0)
cái đoạn\(-xy\left(x+1\right)\)đổi x+1 thành y+1 nha mik đánh nhầm
Đúng 0
Bình luận (0)
1/ cho \(^{5x^2+y^2+4xy+4x+4y-1=0}\)
tìm giá trị lớn nhất của S=2x+y-2 và giá trị x,y
2/cho \(x^2+2xy+7.\left(x+y\right)+2y^2+10=0\)
tìm giá trị lớn nhất của S=x+y+1 và giá trị x,y
3/ cho \(3x^2+y^2+2xy+4=7x+3y\)
tìm giá trị lớn nhất của S=x+y+1