Cô Loan hay thầy gv giúp em với!
tìm : \(ab=a+b=a.b=a:b\)
Giúp em với!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
Tìm tất cả các số nguyên dương ( a, b) thỏa mãn điều kiện
\(\dfrac{a^2+b}{a.b-1}\) là số nguyên dương .
P/s: Em nhờ quý thầy cô giáo gợi ý và giúp đỡ em tham khảo với ạ!
Em cám ơn nhiều lắm ạ!
\(a^2+b⋮ab-1\Rightarrow b\left(a^2+b\right)-a\left(ab-1\right)⋮ab-1\)
\(\Rightarrow a+b^2⋮ab-1\)
Do đó, vai trò của a và b là hoàn toàn như nhau.
TH1: \(a=b\Rightarrow\dfrac{a^2+a}{a^2-1}\in Z\Rightarrow\dfrac{a}{a-1}\in Z\Rightarrow1+\dfrac{1}{a-1}\in Z\)
\(\Rightarrow a=2\Rightarrow a=b=2\)
TH2: \(b>a\Rightarrow b\ge a+1\)
Do \(a^2+b⋮ab-1\Rightarrow a^2+b\ge ab-1\) (nếu \(a< b\) ta sẽ xét với \(a+b^2⋮ab-1\) cho kết quả tương tự nên ko cần TH3 \(a>b\))
\(a^2-1+2\ge ab-b\Rightarrow\left(a-1\right)\left(a+1\right)+2\ge b\left(a-1\right)\)
\(\Rightarrow\left(a-1\right)\left(b-a-1\right)\le2\)
\(\Rightarrow\left(a-1\right)\left(b-a-1\right)=\left\{0;1;2\right\}\)
TH2.1: \(\left(a-1\right)\left(b-a-1\right)=0\Rightarrow\left[{}\begin{matrix}a=1\\b=a+1\end{matrix}\right.\)
- Với \(a=1\Rightarrow\dfrac{b+1}{b-1}\in Z\Rightarrow1+\dfrac{2}{b-1}\in Z\Rightarrow b=\left\{2;3\right\}\)
\(\Rightarrow\left(a;b\right)=\left(1;2\right);\left(1;3\right)\) (và 2 bộ hoán vị \(\left(2;1\right);\left(3;1\right)\) ứng với \(a>b\), lần sau sẽ hoán vị nghiệm luôn ko giải thích lại)
- Với \(b=a+1\Rightarrow\dfrac{a^2+a+1}{a^2+a-1}\in Z\Rightarrow1+\dfrac{2}{a^2+a-1}\in Z\)
\(\Rightarrow a^2+a-1=\left\{1;2\right\}\Rightarrow a=1\Rightarrow b=2\) giống như trên
TH2.2: \(\left(a-1\right)\left(b-a-1\right)=1\Rightarrow\left\{{}\begin{matrix}a-1=1\\b-a-1=1\end{matrix}\right.\) \(\Rightarrow\left(a;b\right)=\left(2;4\right);\left(4;2\right)\)
TH2.3: \(\left(a-1\right)\left(b-a-1\right)=2=2.1=1.2\)
\(\Rightarrow\left(a;b\right)=\left(3;5\right);\left(5;3\right);\left(2;5\right);\left(5;2\right)\)
Vậy các bộ số thỏa mãn là: \(\left(1;2\right);\left(2;1\right);\left(1;3\right);\left(3;1\right);\left(2;2\right);\left(2;5\right);\left(5;2\right);\left(3;5\right);\left(5;3\right)\)
Có tồn tại hay không các số \(a;b;c\in Z\) sao cho
\(a^2+b^2+c^2-ab-bc-ca=30014\) ?
P/s: Em xin phép nhờ quý thầy cô giáo và các bạn gợi ý giúp đỡ em với ạ!
Em cám ơn nhiều lắm ạ!
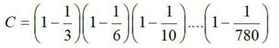
Có anh chị hay thầy cô nào giúp em với ạ.
\(C=\left(1-\dfrac{1}{3}\right)\left(1-\dfrac{1}{6}\right)\left(1-\dfrac{1}{10}\right)...\left(1-\dfrac{1}{780}\right)\)
\(=\dfrac{2}{3}.\dfrac{5}{6}.\dfrac{9}{10}...\dfrac{779}{780}=\dfrac{2.2}{3.2}.\dfrac{5.2}{6.2}.\dfrac{9.2}{10.2}...\dfrac{779.2}{780.2}\)
\(=\dfrac{4}{6}.\dfrac{10}{12}.\dfrac{18}{20}...\dfrac{1558}{1560}=\dfrac{1.4}{2.3}.\dfrac{2.5}{3.4}.\dfrac{3.6}{4.5}...\dfrac{38.41}{39.40}\)
\(=\dfrac{1.2.3...38}{2.3.4...39}.\dfrac{4.5.6...41}{3.4.5...40}=\dfrac{1}{39}.\dfrac{41}{3}=\dfrac{41}{117}\)
\(C=\left(1-\dfrac{2}{6}\right)\left(1-\dfrac{2}{12}\right)\left(1-\dfrac{2}{20}\right)...\left(1-\dfrac{2}{1560}\right)\)
\(=\left(1-\dfrac{2}{2.3}\right)\left(1-\dfrac{2}{3.4}\right)\left(1-\dfrac{2}{4.5}\right)...\left(1-\dfrac{2}{39.40}\right)\)
Ta có: \(1-\dfrac{2}{n\left(n+1\right)}=\dfrac{n\left(n+1\right)-2}{n\left(n+1\right)}=\dfrac{n^2+n-2}{n\left(n+1\right)}=\dfrac{\left(n-1\right)\left(n+2\right)}{n\left(n+1\right)}\)
Do đó:
\(C=\dfrac{1.4}{2.3}.\dfrac{2.5}{3.4}.\dfrac{3.6}{4.5}...\dfrac{38.41}{39.40}\)
\(=\dfrac{1.2.3...38}{2.3.4...39}.\dfrac{4.5.6...41}{3.4.5...40}=\dfrac{1}{39}.\dfrac{41}{3}=\dfrac{41}{117}\)
Cho hai số nguyên dương \(a;b\) với \(b>1\) và thỏa mãn điều kiện \(A=\dfrac{a^2}{2.a.b^2-b^3+1}\) là số nguyên dương. Chứng minh rằng \(A\) là số chính phương.
P/s: Em xin phép nhờ quý thầy cô giáo và các bạn yêu toán gợi ý giúp đỡ em với ạ!
Em cám ơn nhiều lắm ạ!
\(\dfrac{a^2}{2ab^2-b^3+1}=m\in Z^+\Rightarrow a^2-2mb^2a.+mb^3-m=0\)
\(\Rightarrow\Delta=4m^2b^4-4mb^3+4m\) là SCP (1)
Ta dễ dàng chứng minh được:
\(4m^2b^4-4mb^3+4m>\left(2mb^2-b-1\right)^2\)
\(\Leftrightarrow4m\left(b^2+1\right)>\left(b+1\right)^2\)
Đúng do: \(2m.2\left(b^2+1\right)\ge2m\left(b+1\right)^2>\left(b+1\right)^2\)
Tương tự, ta cũng có: \(4m^2b^4-4mb^3+4m< \left(2mb^2-b+1\right)^2\)
\(\Leftrightarrow\left(b-1\right)^2+4m\left(b^2-1\right)>0\) (luôn đúng với b>1;m>0)
\(\Rightarrow\left(2mb^2-b-1\right)^2< 4m^2b^4-4mb^3+4m< \left(2mb^2-b+1\right)^2\)
\(\Rightarrow4m^2b^4-4mb^3+4m=\left(2mb^2-b\right)^2\)
\(\Rightarrow b^2=4m\)
\(\Rightarrow b\) chẵn \(\Rightarrow b=2k\Rightarrow m=k^2\)
Thế vào (1) \(\Rightarrow a^2-8k^4a+8k^5-k^2=0\)
\(\Leftrightarrow\left(a-k\right)\left(a-8k^4+k\right)=0\Rightarrow\left[{}\begin{matrix}a=k\\a=8k^4-k\end{matrix}\right.\)
Vậy nghiệm của pt là: \(\left(a;b\right)=\left(k;2k\right);\left(8k^4-k;2k\right)\) với k nguyên dương
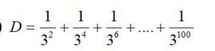
Có anh chị hay thầy cô nào giúp em nốt câu này với ạ, em cảm ơn.
Đề yêu cầu gì vậy em? Rút gọn?
\(D=\dfrac{1}{3^2}+\dfrac{1}{3^4}+\dfrac{1}{3^6}+...+\dfrac{1}{3^{100}}\)
\(\Rightarrow9D=1+\dfrac{1}{3^2}+\dfrac{3}{3^4}+...+\dfrac{1}{3^{98}}\)
\(\Rightarrow9D-D=1-\dfrac{1}{3^{100}}\)
\(\Rightarrow8D=1-\dfrac{1}{3^{100}}\)
\(\Rightarrow D=\dfrac{1}{8}\left(1-\dfrac{1}{3^{100}}\right)\)
Tìm chữ số a và b để \(ababab4\) \(⋮\) \(72\)
Thầy cô giúp em với ạ cuối tuần em nộp bài rồi
Ta thấy tổng các chữ số của số \(\overline{ababab4}\) là \(a+b+a+b+a+b+4\)
\(=3a+3b+4\).
Do \(3a,3b⋮3\) và 4 không chia hết cho 3 nên \(3a+3b+4⋮̸3\). Điều này có nghĩa là số \(\overline{ababab4}\) không thể chia hết cho 3 dù a, b có là chữ số nào. Vì thế, không tồn tại chữ số a, b nào để \(\overline{ababab4}\) chia hết cho 72.
em hỏi xíu là vì sao lại xét dấu hiệu chia hết cho 3 ạ?
giúp mình với !!!
Tìm 2 số huữ tỷ a và b, sao cho :a+b=a.b=a:b
Tìm 2 số a,b (b khác 0) biết a+b = a.b = a:b
Làm ơn giúp mình với
bài của bạn giống bài của Vũ Thị Thúy, mìh đã giải cho bạn ấy rồi đó. bn xem bài của bn ấy nhé
K ĐÚNG NHA
Đặt a + b = ab = a : b = k
Ta có : a/b = k => a = kb
=> kb + b = kbb = k
=> (k + 1) b = kb2 = k
Từ kb2 = k
=> kb2 - k = 0
=> k (b2 - 1) = 0
=> k = 0 hoặc b2 - 1 = 0
=> k = 0 hoặc b = ±1
Trường hợp k = 0 => a = 0
=> 0 + b = 0 => b = 0 (loại vì b ≠ 0)
Trường hợp b = 1
=> a + 1 = a . 1 => a + 1 = a => 1 = 0 (vô lí)
=> b = 1 ko thỏa mãn
Trường hợp b = -1
=> a - 1 = a (-1) => a - 1 = -a => a - 1 +a = 0 => 2a - 1 = 0 => a = 1/2
ta có:a+b=ab
=>a=ab-b=b(a-1)
=>a/b=a-1
mà theo đề:a+b=a/b
=>a-1=a+b
=>a+(-1)=a+b
=>b=-1
thay b=-1 vào a+b=ab
=>a+(-1)=a.(-1)
=>a+(-1)=-a
=>(-a)-a=-1=>-2a=-1=>a=-1/-2=1/2=0,5
vậy a=0,5;b=-1
CTV và GV ơi giúp em vs
Chứng minh rằng ΔABC đồng dạng với một tam giác có ba cạnh lần lượt bằng độ dài đường cao ứng với ba đỉnh của tam giác ABC.
Cô thầy ơi cứu em :(