Đường thẳng y=x-3 đi qua điểm
A.(1;2)
B.(1;-2)
C.(2;2)
D.(3;-2)
Những câu hỏi liên quan
cho đường thẳng y=mx+m-1
a) Tìm m để đường thẳng đã cho đi qua điểm
A(−3;2)
a) Chứng minh đường thẳng đã cho luôn đi qua một điểm cố định
b) Tìm m để đường thẳng đã cho tạo với hai trục tọa độ một tam giác có diện tích bằng 2.
BÀI 5.Cho hai điểmA,Bphân biệt. Hãy vẽ ba đường tròn đi qua hai điểmA,B.Tâm của ba đường tròn này nằm trên đường thẳng nào?
Tâm của ba đường tròn này sẽ nằm trên đường trung trực của AB
Đúng 0
Bình luận (1)
5 tháng 11 2021 lúc 21:42
Câu 24: Đường thẳng 3x – 2y = 5 đi qua điểm
A.(1;-1) B. (5;-5) C. (1;1) D.(-5;5)
cho trước 6 điểm vẽ các đường thẳng đi qua các cặp điểma nếu trong 6 điểm đó k có 3 điểm nào thẳng hàng thì vẽ được bao nhiêu đường thẳng b nếu trong 6 điểm có đúng 3 điểm thẳng hàng thì sẽ vẽ được bao nhiêu đường thẳng
cho đường thẳng d y = (m + 2) x + m Tìm m để d
a, song song với đường thẳng d1 : y = -2 x + 3
b ,vuông góc với đường thẳng d2 : y = 1 / 3 x + 1
C, đi qua điểm N( 1,3)
D, Tìm điểm cố định Mà D luôn đi qua với mọi m
\(a,d//d_1\Leftrightarrow\left\{{}\begin{matrix}m+2=-2\\m\ne3\end{matrix}\right.\Leftrightarrow m=-4\\ b,d\perp d_2\Leftrightarrow\dfrac{1}{3}\left(m+2\right)=-1\Leftrightarrow m+2=-3\Leftrightarrow m=-5\\ c,d.qua.N\left(1;3\right)\Leftrightarrow x=1;y=3\Leftrightarrow3=m+2+m\\ \Leftrightarrow2m=1\Leftrightarrow m=\dfrac{1}{2}\)
Đúng 2
Bình luận (1)
\(d,\) Gọi điểm đó là \(A\left(x_1;y_1\right)\)
\(\Leftrightarrow y_1=\left(m+2\right)x_1+m\\ \Leftrightarrow y_1-mx_1-2x_1-m=0\\ \Leftrightarrow-m\left(x_1+1\right)+y_1-2x_1=0\\ \Leftrightarrow\left\{{}\begin{matrix}x_1+1=0\\y_1-2x_1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_1=-1\\y_1=-2\end{matrix}\right.\)
Vậy \(A\left(-1;-2\right)\) luôn đi qua D với mọi m
Đúng 2
Bình luận (0)
Tìm hệ số góc của đường thường `y=ax+b`, biết
Đường thẳng `y=ax+b` đi qua `P(-1;-3)` và đi qua giao điểm của hai đường thẳng `y=x-7;y=-4x+3`
Tọa độ giao điểm của hai đường thẳng y=x-7 và y=-4x+3 là:
\(\left\{{}\begin{matrix}x-7=-4x+3\\y=x-7\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x+4x=7+3\\y=x-7\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}5x=10\\y=x-7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=2-7=-5\end{matrix}\right.\)
Thay x=2 và y=-5 vào y=ax+b, ta được:
a*2+b=-5
=>2a+b=-5(1)
thay x=-1 và y=-3 vào y=ax+b, ta được:
a*(-1)+b=-3
=>-a+b=-3(2)
Từ (1),(2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}2a+b=-5\\-a+b=-3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3a=-2\\a-b=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-\dfrac{2}{3}\\b=a-3=-\dfrac{2}{3}-3=-\dfrac{11}{3}\end{matrix}\right.\)
Vậy: (d): \(y=-\dfrac{2}{3}x-\dfrac{11}{3}\)
Đúng 1
Bình luận (0)
Lập phương trình đường thẳng y= ax + b,biế
1. Δ đi qua điểm A(3;-2) và B(2;1)
2. Δ đi qua điểm E(3;3) và song song với đường thẳng d : y=-3x+2 3. ΔΔ đi qua điểm G(1;1) và vuông góc với đường thẳng d: y=-x+1
1: Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}3a+b=-2\\2a+b=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-3\\b=1-2a=1-2\cdot\left(-3\right)=7\end{matrix}\right.\)
2: Vì (d)//y=-3x+2 nên a=-3
Vậy: y=-3x+b
Thay x=3 và y=3 vào y=-3x+b, ta được:
b-9=3
hay b=12
Đúng 3
Bình luận (2)
Cho các điểm
A(1;2) ; B(2;2) ; C(3;3 ) . Viết phương trình đường thẳng d đi qua A và vuông
góc với BC .
\(\left\{{}\begin{matrix}2a+b=2\\3a+b=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-a=-1\\2a+b=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=1\\b=0\end{matrix}\right.\)
Vậy: (BC): y=x
Gọi (d): y=ax+b là ptđt cần tìm
Vì (d) vuông góc với (BC) nên a=-1
Vậy: (d): y=-x+b
Thay x=1 và y=2 vào (d), ta được:
b-1=2
hay b=3
Đúng 2
Bình luận (1)
Trong Hình 6 có ba đoạn thẳng được đánh số (1), (2), (3) và hai điểm A, B
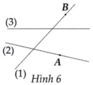
Hãy xác định đường thẳng nào là đường thẳng x, y , z biết
- Đường thẳng x đi qua điểm A;
- Đường thẳng y chứa điểm B;
- Đường thẳng z không đi qua hai điểm A và B
Đường thẳng x là đường thẳng số (2). Đường thẳng y là đường thẳng số (1). Đường thẳng z là đường thẳng số (3)
Đúng 0
Bình luận (0)