Cho tam giác ABC có BD và CE là hai đường phân giác. Cm tam giác ABC cân BD CE
Đọc tiếp
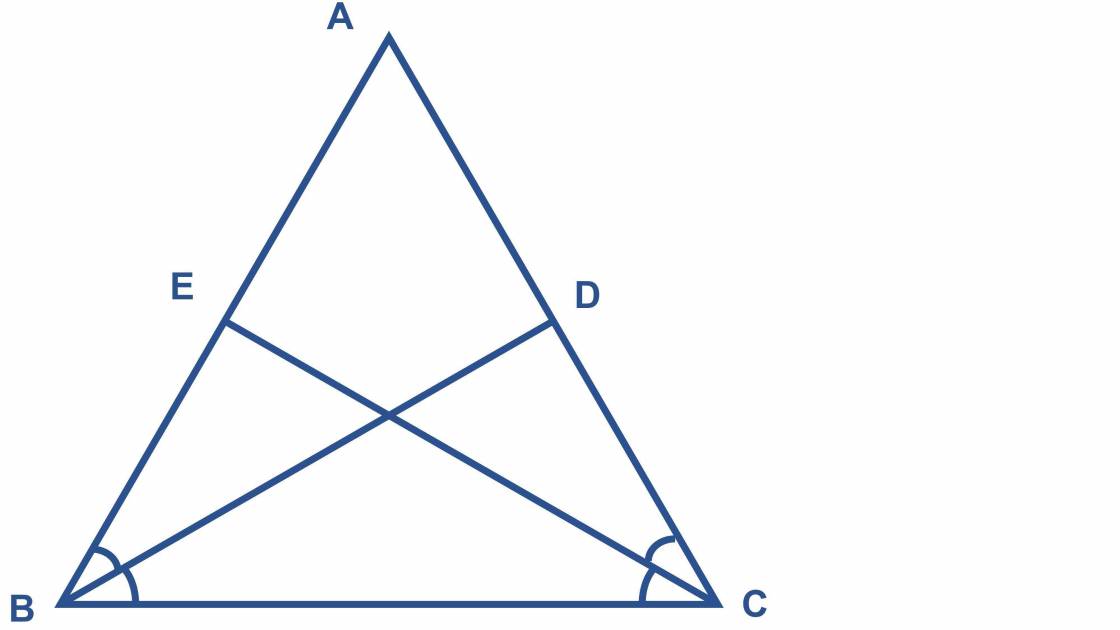
Cho tam giác ABC có BD và CE là hai đường phân giác. Cm tam giác ABC cân <=> BD = CE
Những câu hỏi liên quan
cho tam giác ABC có BD và CE là 2 đường cao hạ từ B,C và BD=CE. H là giao điểm của BD và CE
a) Chứng minh tam giác ABC cân tại A
b) AH là phân giác góc BAC
cho tam giác abc cân tại a có 2 đường cao BD và CE cắt nhâu tại H a, CM: BDCE b, CM: tam giác BHC cân c, CM: AH là đường trung trực của BC d, Trên tia BD lấy điểm K sao cho D là trung điểm BK So sánh góc ECB và góc DKC
Đọc tiếp
cho tam giác abc cân tại a có 2 đường cao BD và CE cắt nhâu tại H a, CM: BD=CE b, CM: tam giác BHC cân c, CM: AH là đường trung trực của BC d, Trên tia BD lấy điểm K sao cho D là trung điểm BK So sánh góc ECB và góc DKC
a: Xét ΔABD vuông tại D và ΔACE vuông tại E có
AB=AC
góc BAD chung
=>ΔABD=ΔACE
=>AD=AE
Xét ΔABC có AE/AB=AD/AC
nên ED//BC
=>BEDC là hình thang
mà BD=CE
nên BEDC là hình thang cân
b: góc ABD+góc DBC=góc ABC
góc ACE+góc ECB=góc ACB
mà góc ABD=góc ACE; góc ABC=góc ACB
nên góc DBC=góc ECB
=>ΔHBC cân tại H
c: AB=AC
HB=HC
=>AH là trung trực của BC
Đúng 0
Bình luận (0)
Cho tam giác ABC Có phân giác BD = phân giác CE. CM tam giác ABC cân
Cho tam giác ABC cân tại A, vẽ các đường phân giác BD và CE
a) CM BD=CE
b) CM ED//BC
tự vẽ hình
a, ta có: góc DCB = góc EBC (t/g ABC cân tại A) => \(\widehat{\frac{DCB}{2}}=\frac{\widehat{EBC}}{2}\Rightarrow DBC=ECB\)
Xét t/g DBC và t/g ECB có:
góc DCB = góc EBC(t/g ABC cận tại A)
BC chung
góc DBC = góc ECB (cmt)
=> t/g DBC=t/g ECB (g.c.g)
=>DB=EC
b, Vì AB=AC (t/g ABC cân tại A), DB=EC (cmt) => AD=AE
=> t/g ADE cân tại A
=> \(\widehat{AED}=\widehat{ADE}=\frac{180^0-\widehat{A}}{2}\)
Mà \(ABC=ACB=\frac{180^o-A}{2}\)
DO đó góc AED=ABC
Mà 2 góc này là 2 góc đồng vị
=> ED//BC
P/s; lười viết kí hiệu góc
Đúng 0
Bình luận (0)
cho tam giác ABC có 2 đườg cao là BD và CE thỏa mãn AC+CE=AB+BD.
CM tam giác ABC cân
Cho tam giác abc cân tại a, hai đường cao BD và CE cắt nhau tại I (d thuộc ac; e thuộc ab).
a) cm BD = CE.
b) CM : tam giác AED là tam giác cân và ed // bc.
c) Biết góc BAC = 70 độ. tính các góc của tam giác ibc.
d) Qua b kẻ tia Bx//CE; qua C kẻ Cy //bd. Bx và Cy cắt nhau tại M. cm IM đi qua trung điểm của BC.
Cho tam giác ABC cân tại A. Kẻ phân giác BD và CE. Có hai tam giác bằng nhau là
các tam giác bằng nhau là:
BDC và CEB
AEC và ADB
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác ABC có BD,CE là các phân giác . CMR : Nếu BD=CE thì tam giác ABC cân tại A
Cho tam giác ABC cân tại A có hai đường trung tuyến BD và CE cắt nhau tại G . Biết BD = CE
a) Chứng minh tam giác GBC là tam giác cân
b) Chứng minh DG + EG > 1/2 BC
Câu này làm thế nào vậy mn
giúp mình với
Đúng 0
Bình luận (0)
xét ΔECB và ΔDBC, ta có :
EC = BD (gt)
\(\widehat{B}=\widehat{C}\) (2 góc đáy của ΔABC cân tại A)
BC là cạnh chung
=> ΔECB = ΔDBC (c.g.c)
=> \(\widehat{GBC}=\widehat{GCB}\) (2 góc tương ứng)
vì ΔGBC có \(\widehat{GBC}=\widehat{GCB}\) nên ⇒ ΔGBC là một tam giác cân (cân tại G)
Đúng 1
Bình luận (1)
cho tam giác abc cân tại a vẽ phân giác góc b cắt ac tại d phân giác góc c cắt ab tại e . i là giao điểm của bd và ce . cm a , tam giác ibc cân. b, bd=ce