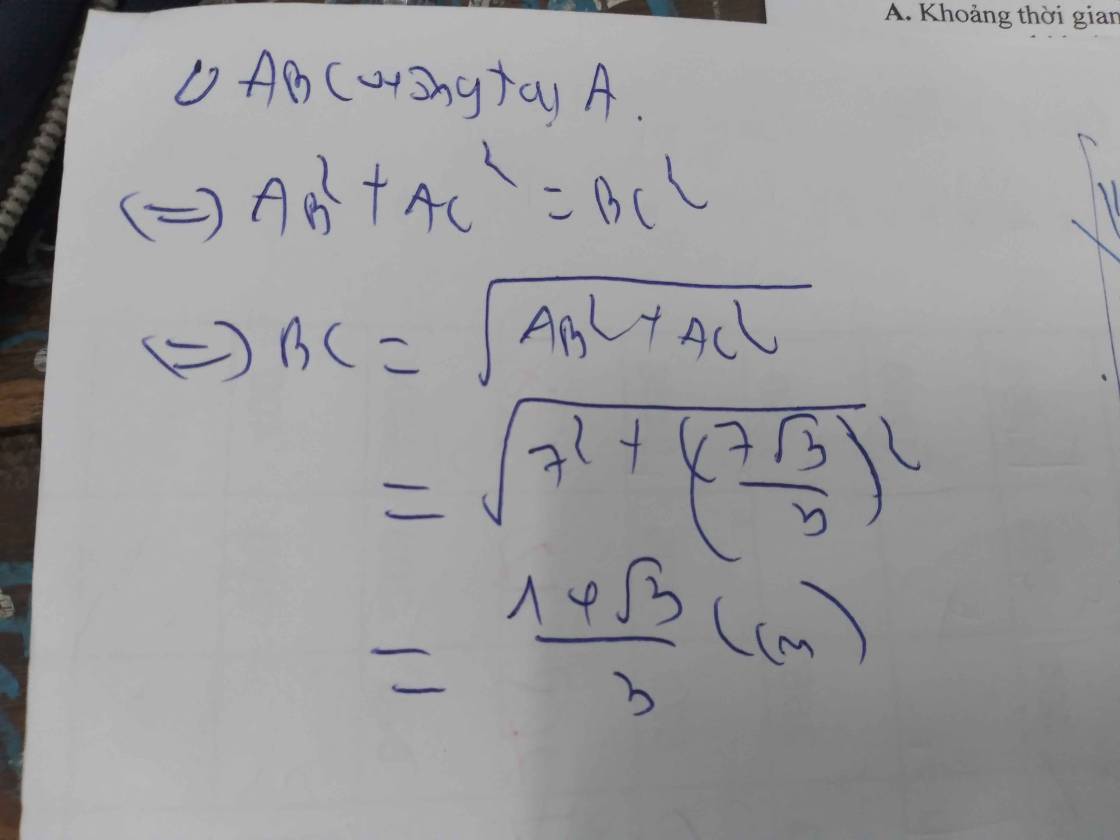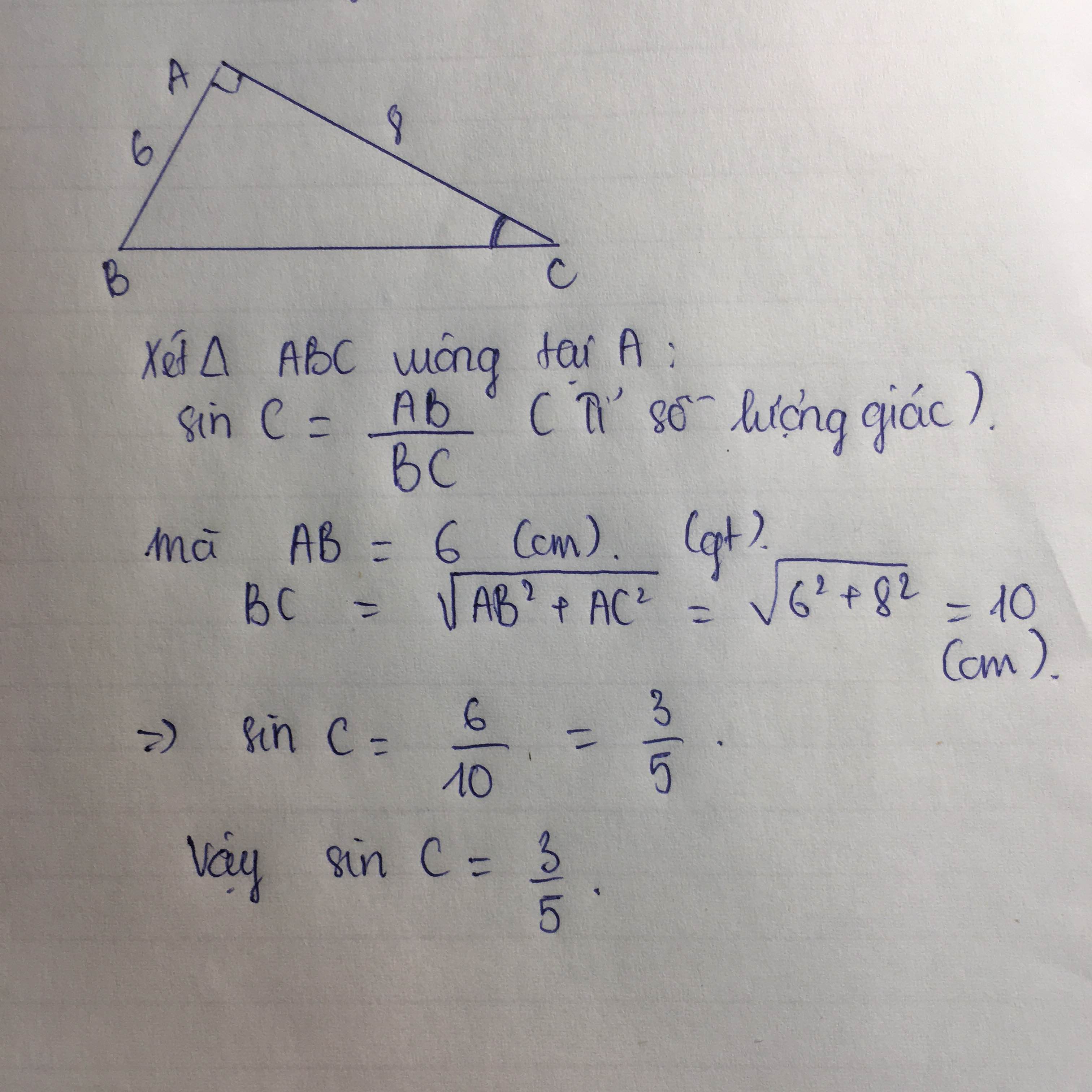Cho tam giác ABC vuông tại A.Biết: B=3C.Tính B,C

Những câu hỏi liên quan
1)Cho tam giác ABC vuông tại A.Biết góc B=60 độ;BC=4.Tính AB,AC,chiều cao AH
2)Cho tam giác ABC vuông tại A.Biết AB=2;góc C=45 độ.Tính AC,BC,chiều cao AH
3)Cho tam giác ABC vuông tại A,Biết AB=3;AC=4.Tính sin C,tan B
Giải giúp mình ạ
Cho tam giác ABC vuông tại A.Biết AC =7cm , góc C =30 độ .giải Tam giác vuông ABC
Cho tam giác ABC cân tại A.Biết góc C =65 độ.Tính góc A
Cho tam giác DEF vuông tại E Biết DE =8cm,DF=17cm
a; Tính EF
b; So sánh các góc của tam giác DEF
1.
Ta có:
\(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)
Mà \(\widehat{B}=\widehat{C}\)
\(\Rightarrow\widehat{A}+\widehat{C}+\widehat{C}=180^0\)
\(\widehat{A}=180^0-2.65^0\)
\(\widehat{A}=50^0\)
2.
Áp dụng định lý pitago, ta có:
\(DF^2=DE^2+EF^2\)
\(\Rightarrow EF=\sqrt{DF^2-DE^2}=\sqrt{17^2-8^2}=\sqrt{225}=15cm\)
Ta có:
\(DF>EF>DE\)
\(\Rightarrow\widehat{E}>\widehat{D}>\widehat{F}\)
Đúng 3
Bình luận (2)
1.
Ta có:
ˆA+ˆB+ˆC=1800A^+B^+C^=1800
Mà ˆB=ˆCB^=C^
⇒ˆA+ˆC+ˆC=1800⇒A^+C^+C^=1800
ˆA=1800−2.650A^=1800−2.650
ˆA=500A^=500
2.
Áp dụng định lý pitago, ta có:
DF2=DE2+EF2DF2=DE2+EF2
⇒EF=√DF2−DE2=√172−82=√225=15cm⇒EF=DF2−DE2=172−82=225=15cm
Ta có:
DF>EF>DEDF>EF>DE
⇒ˆE>ˆD>ˆF
Đúng 3
Bình luận (0)
Cho tam giác ABC, biết 6C=4B=3C.Tính A,B,C?
cho tam giác abc vuông tại a.biết sinb=3/5.tính các tỉ số lượng giác của b
GIẢI:
sinB=3/4 =>cosC=3/5
Ta có: cos^2 C+sin^2 C=1 => sin^2C=1-(3/5)^2=7/16
=>sinC=(√7)/5
=>tanC=sinC/cosC=[(√7)/5]/(3/)=(√7)/5
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A.Biết AB=6:BC=10
a,Tính AC
b,Tinh phân giác góc C cắt AB tại E,Kẻ EM vuông góc với BC
Chứng minh tam giác CEM =tam giác CEA
c,Gọi giao điểm EM và AC tại H
Chứng minh CE vuông góc AB
cho tam giác ABC vuông góc tại A.biết AH vuông góc BC(H thuộc BC),phân giác góc C và góc BAH cắt nhau tại I .tính góc AIC
Cho tam giác ABC vuông tại A.Biết AB=6cm,AC=8cm.Tính sinC
Áp dụng định lý Pytago vào ΔABC vuông tại A ta có:
\(BC^2=AB^2+AC^2=6^2+8^2\Leftrightarrow BC=10\left(cm\right)\)
\(\Rightarrow sinC=\dfrac{AB}{BC}=\dfrac{6}{10}=\dfrac{3}{5}\)
Đúng 0
Bình luận (0)
BC2=AB2+AC2=62+82⇔BC=10(cm)BC2=AB2+AC2=62+82⇔BC=10(cm)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A.Biết \(\frac{AB}{AC}=\frac{5}{7}\),đường cao AH=15cm
a)Tính HB,HC
b)Tính chu vi tam giác ABC
a) Ta thấy: \(AB.AC=BC.AH\)
\(\Leftrightarrow AB^2.AC^2=BC^2.AH^2\)
\(\Leftrightarrow AH^2=\frac{AB^2.AC^2}{BC^2}\)
\(\Leftrightarrow AH^2=\frac{AB^2.AC^2}{AB^2+AC^2}\)
\(\Leftrightarrow\frac{1}{AH^2}=\frac{AB^2+AC^2}{AB^2.AC^2}=\frac{1}{AB^2}+\frac{1}{AC^2}\)
Ta có: \(\frac{AB}{AC}=\frac{5}{7}\Rightarrow AB:AC=\frac{5}{7}\Rightarrow AB=\frac{5}{7}AC\)
Áp dụng công thức trên: \(\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}\Leftrightarrow\frac{1}{15^2}=\frac{1}{\frac{25}{49}AC^2}+\frac{1}{AC^2}\Leftrightarrow\frac{1}{225}=\frac{49}{25}.\frac{1}{AC^2}+\frac{1}{AC^2}\Leftrightarrow\frac{1}{225}=\frac{1}{AC^2}\left(\frac{49}{25}+1\right)\)
\(\Rightarrow\frac{1}{225}=\frac{1}{AC^2}.\frac{74}{25}\Rightarrow\frac{1}{AC^2}=\frac{1}{225}.\frac{25}{74}=\frac{1}{666}\Rightarrow AC^2=666\Rightarrow AC=\sqrt{666}=3\sqrt{74}cm\)
Do đó: \(AB=\frac{5}{7}.3\sqrt{74}=\frac{15\sqrt{74}}{7}cm\)
Xét tam giác ABH có: \(AH^2+BH^2=AB^2\Leftrightarrow15^2+BH^2=\left(\frac{15\sqrt{74}}{7}\right)^2\Leftrightarrow BH^2=\frac{16650}{49}-225=\frac{5625}{49}\)
\(\Rightarrow BH=\frac{\sqrt{5625}}{\sqrt{49}}=\frac{75}{7}cm\)
Xét tam giác ACH có: \(AH^2+HC^2=AC^2\Leftrightarrow15^2+HC^2=666\Leftrightarrow HC^2=666-225=441\)
\(\Rightarrow HC=\sqrt{441}=21cm\)
Vậy: \(BH=\frac{75}{7}cm\) và \(HC=21cm\)
b) Chu vi tam giác ABC là: \(AB+AC+BC=\frac{15\sqrt{74}}{7}+3\sqrt{74}+21+\frac{75}{7}\approx76cm\)
Đúng 0
Bình luận (0)
Vì tam giác ABC vuông tại A => góc B + góc C = 90o
Vì tam giác HAC vuông tại H => góc HAC + góc C = 90o
=> góc HAC = góc B
Xét tam giác HAC và tam giác HBA có:
góc HAC = góc B (cmt)
góc AHC = góc AHB (=90o)
=> tam giác HAC đồng dạng với tam giác HBA (TH3)
=> \(\frac{AC}{AB}=\frac{AH}{BH}=\frac{HC}{AH}=\frac{7}{5}\)
=> \(HC=15.\frac{7}{5}=21\left(cm\right);HB=15.\frac{5}{7}=\frac{75}{7}\left(cm\right)\)
Sau đó tính AB; AC; BC. Ngại là lắm, làm nốt nhá ._.
Đúng 0
Bình luận (0)
a) Ta có: \(\frac{AB}{AC}=\frac{5}{7}\Rightarrow AB:AC=\frac{5}{7}\Rightarrow AB=\frac{5}{7}AC\)
Áp dụng công thức: \(\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}\Leftrightarrow\frac{1}{15^2}=\frac{1}{\frac{25}{49}AC^2}+\frac{1}{AC^2}\Leftrightarrow\frac{1}{225}=\frac{49}{25}.\frac{1}{AC^2}+\frac{1}{AC^2}\Leftrightarrow\frac{1}{225}=\frac{1}{AC^2}\left(\frac{49}{25}+1\right)\)
\(\Rightarrow\frac{1}{225}=\frac{1}{AC^2}.\frac{74}{25}\Rightarrow\frac{1}{AC^2}=\frac{1}{225}.\frac{25}{74}=\frac{1}{666}\Rightarrow AC^2=666\Rightarrow AC=\sqrt{666}=3\sqrt{74}cm\)
Do đó: \(AB=\frac{5}{7}.3\sqrt{74}=\frac{15\sqrt{74}}{7}cm\)
Suy ra: \(CH=21cm\) và \(BH=\frac{75}{7}cm\) ( Áp đụng định lý Pi - ta go )
b) Chu vi tam giác ABC là: AB + AC + BC = \(\frac{15\sqrt{74}}{7}+3\sqrt{74}+21+\frac{75}{7}\approx76cm\)
Cũng k biết đúng k nữa =.=
Đúng 0
Bình luận (0)