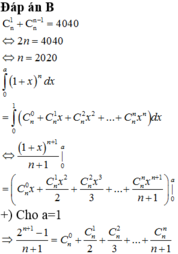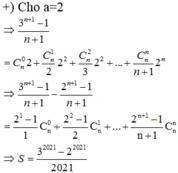Cho S = 1-2+22-23+... - 22013 + 22014 . Khi đó 3S-1=2n Vậy n =

Những câu hỏi liên quan
Cho S = 1 - 2 + 22 -23 +...+22012 - 22013 . Tính 3S - 22014
\(S=1-2+2^2-2^3+...+2^{2012}-2^{2013}\)
\(\Rightarrow2S=2-2^2+2^3-2^4+...+2^{2013}-2^{2014}\)
\(\Rightarrow2S+S=2-2^2+2^3-...-2^{2014}+1-2^2-2^3+...-2^{2013}\)
\(\Rightarrow3S=1-2^{2014}\)\(\Rightarrow3S-2^{2014}=1-2^{2015}\)
Đúng 5
Bình luận (0)
Cho S=1-2+2^2-2^3+2^4-2^5+...+2^{2013}-2^{2014}.S=1−2+22−23+24−25+...+22013−22014. Khi đó 1-3S=2^x.1−3S=2x.
Vậy x=...............................
ta có: \(S=1-2+2^2-2^3+2^4-2^5+...+2^{2013}-2^{2014}\)
\(\Rightarrow2S=2-2^2+2^3-2^4+2^5-2^6+...+2^{2014}-2^{2015}\)
=> 2S + S = -22015 + 1
=> 3S = -22015 + 1
=> 3S - 1 = -22015
=> 1 - 3S = 22015
( cn về S = 1 - 2 + 22 - 23 + 24-25+...+22013 - 22014 mk vx chưa hiểu quy luật của nó lắm, thật lòng xl bn nha! mk chỉ bk z thoy!)
Đúng 0
Bình luận (0)
Tính giá trị của biểu thức sau :
B=22014-22013-22012-....-23-22-3
Cho n là nghiệm của
C
1
n
+
C
n
n
-
1
4040
, khi đó tổng
S
2
1
-
1
1
C
n
0
+...
Đọc tiếp
Cho n là nghiệm của C 1 n + C n n - 1 = 4040 , khi đó tổng S = 2 1 - 1 1 C n 0 + 2 2 - 1 2 C n 1 + 2 3 - 1 3 C n 2 + . . . + 2 n + 1 - 1 n + 1 C n n bằng
A. 3 2022 + 2 2021
B. 3 2021 - 2 2021 2021
C. 3 2020 - 2 2021 2021
D. 3 2021 - 2 2021 2020
Cho n là nghiệm của
C
n
1
+
C
n
n
-
1
4040
. Khi đó tổng
S
2
1
-
1
1
C
n
0
+
2...
Đọc tiếp
Cho n là nghiệm của C n 1 + C n n - 1 = 4040 . Khi đó tổng S = 2 1 - 1 1 C n 0 + 2 2 - 1 2 C n 1 + 2 3 - 1 3 C n 2 + . . . + 2 n + 1 - 1 n + 1 C n n bằng

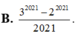
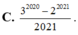
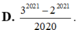
Cho s=1-2+2^2-2^3+......-2^2013+2^2014 Khi đó 3s-1=2^n .vậy n=
Tìm số dư trong phép chia 2 2014 cho
1 + 2 + 2 2 + 2 3 + . . . + 2 2011
cho S = 1-2+2^2-2^3+...-2^2013+2^2014.Khi đó 3S - 1 =2^n. Vậy n =...
2S = 2 - 22 + 23 - 24 +...- 22014 + 22015
=> S + 2S = 1 + 22015 => 3S = 1 + 22015 => 3S - 1 = 22015 => n = 2015
Đúng 0
Bình luận (0)
b) Tìm số dư trong phép chia 2 2014 cho 1 + 2 + 2 2 + 2 3 + . . . + 2 2011
xam xi
M = 1 + 22 + 23 + ... + 22012 / 22014 - 2
Tính M
Đặt N = 1 + 2 + 22 +...+ 22012
2N = 2 + 22 + 23 +...+ 22013
2N - N = (2 + 22 + 23+....+ 22013) - (1 + 2 + 22 +....+ 22012)
N = 22013 - 1
Thay N vào M ta được:
\(M=\dfrac{2^{2013}-1}{2^{2014}-2}=\dfrac{2^{2013}-1}{2\left(2^{2013}-1\right)}=\dfrac{1}{2}\)
Đúng 5
Bình luận (1)
Đặt \(N=1+2+2^2+...+2^{2012}\)
\(2N=2+2^2+2^3+...+2^{2013}\)
\(2N-N=\left(2+2^2+2^3+...+2^{2013}\right)-\left(1+2+2^2+...+2^{2012}\right)\)
\(N=2^{2013}-1\)
Thay N vào M ta được:
\(M=\dfrac{2^{2013-1}}{2^{2014}-2}=\dfrac{2^{2013}-1}{2\left(2^{2013}-1\right)}=\dfrac{1}{2}\)
Đúng 1
Bình luận (0)
Tham khảo link: https://olm.vn/hoi-dap/detail/80564627052.html
Đúng 4
Bình luận (1)