384 trên 208 = a phần 13
hãy cho hai phân số trên bằng nhau
Cho 2 phân số =nhau : 384 phần 208 = a phần 13
khi đó a =
Cho hai phân số bằng nhau : 384 phần 28 = a phần 13. tim a.
;
\(\frac{384}{28}=\frac{96}{7}=\frac{196}{14}\)
=> sai đề
\(\frac{384}{28}\)=\(\frac{a}{13}\)
=>\(\frac{96}{7}\)=\(\frac{a}{13}\)
=>96x13=7xa
=>1248=7xa
=>1248:7=a
=>\(\frac{1248}{7}\)=a
Vậy a=\(\frac{1248}{7}\)
cac ban giup minh voi
cho hai phan so bang nhau 384/208= a/13
Tổ Hai được phân công trồng cây trên một mảnh đất. Các bạn chia mảnh đất thành 12 phần bằng nhau và trồng cây như sau:
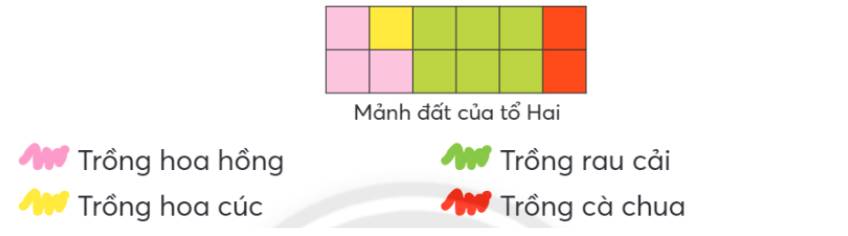
Viết phân số chỉ phần đất trồng mỗi loại cây trên mảnh đất (theo mẫu).
Mẫu: Hoa hồng được trồng trên $\frac{3}{{12}}$ mảnh đất.
Hoa hồng được trồng trên $\frac{3}{{12}}$ mảnh đất.
Hoa cúc được trồng trên $\frac{1}{{12}}$ mảnh đất.
Rau cải được trồng trên $\frac{6}{{12}}$ mảnh đất.
Cà chua được trồng trên $\frac{2}{{12}}$ mảnh đất.
Cho hai phân số: 2/x; 2/x+2. Với giá trị nguyên nào của x thì hai phân số trên bằng nhau.
Nếu:\(\frac{2}{x}=\frac{2}{x+2}\)
=>\(2x+4=2x\)
\(0x=-4\)(vô lí)
Vậy không có giá trị n để thỏa mãn đề bài
cho 2 phân số bằng nhau: 384 phan 208 = a phần 13. khi đó: a =......
rút gọn \(\frac{384}{208}\) = \(\frac{384\div16}{208\div16}\) = \(\frac{24}{13}\)
vậy a = 24
\(\frac{384}{208}=\frac{a}{13}\Leftrightarrow384.13=208.a\Rightarrow a=\frac{384.13}{208}=\frac{4992}{208}=24\)
Vậy a = 24
cho 2 phân số 5 phần 8 và 4 phần 5 tìm phân số a trên b sao cho đem phần số 5 phần 8 cộng a trên b và 4 phần 5 trừ a trên b thì được 2 phân số mà phân số này gấp 2 lần phân số kia
cho 208/384=a-2/24.Vay a=
\(\frac{208}{384}=\frac{a-2}{24}\Leftrightarrow208\times24=\left(a-2\right)384 \)
<=> 384a - 768 = 4992
<=> 384a = 5760
<=> a=5760/384
a=15
Trong mặt phẳng tọa độ, cho hình chữ nhật H có một cạnh nằm trên trục hoành và có hai đỉnh trên một đường chéo là A - 1 ; 0 và C a ; a với a > 0. Biết rằng đồ thị hàm số y = x chia hình H thành hai phần có diện tích bằng nhau, tìm a
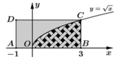
A. a = 1 2
B. a = 3
C. a = 4
D. a = 9
Từ hình vẽ ta suy ra B(a;0)
Hình chữ nhật ABCD có AB = a + 1 và AD = a nên có diện tích S = a (a+1)
Diện tích miền gạch sọc: 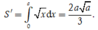
Theo giả thiết, ta có ![]()
Chọn B.