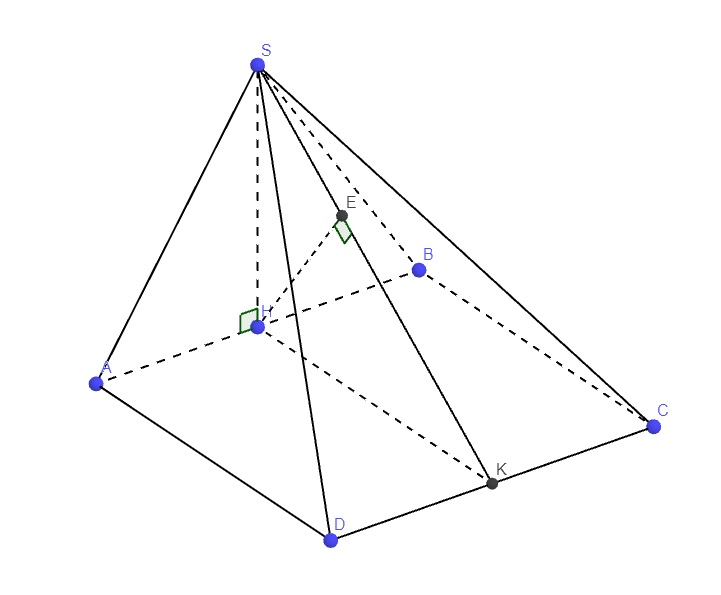
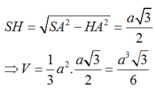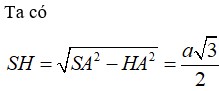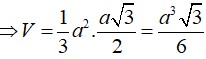Chóp SABCD có (SAD)⏊(ABCD), △SAD đều cạnh a, ABCD là hình vuông, M là trung điểm AB. Tính d(SM,AC)

Những câu hỏi liên quan
Cho hình chóp SABCD có đáy ABCD là hình vuông cạnh a. Hình chiếu vuông góc của S lên mặt phẳng ABCD trùng với trung điểmH của cạnh AB. CHo SH=a√3/3. Gọi K là trung điểm CD
a) CM : (SAD)⊥(SAB)
b) Gọi α là góc giữa SM và (ABCD) . Xác định và tính tan α
c)Xác định và tính góc giữa 2 mặt phẳng (ABCD) và (SCD)
d) Tính khoảng cách từ H đến (SCD)
a.
\(\left\{{}\begin{matrix}SH\perp\left(ABCD\right)\Rightarrow SH\perp AD\\AB\perp AD\left(gt\right)\end{matrix}\right.\) \(\Rightarrow AD\perp\left(SAB\right)\)
Mà \(AD\in\left(SAD\right)\Rightarrow\left(SAD\right)\perp\left(SAB\right)\)
b.
M là điểm nào nhỉ?
c.
\(\left\{{}\begin{matrix}SH\perp\left(ABCD\right)\Rightarrow SH\perp CD\\HK\perp CD\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SHK\right)\)
Mà \(CD=\left(SCD\right)\cap\left(ABCD\right)\)
\(\Rightarrow\widehat{SKH}\) là góc giữa (SCD) và (ABCD)
\(HK=AD=a\Rightarrow tan\widehat{SKH}=\dfrac{SH}{HK}=\dfrac{\sqrt{3}}{3}\Rightarrow\widehat{SKH}=30^0\)
d.
Từ H kẻ \(HE\perp SK\) (E thuộc SK)
\(CD\perp\left(SHK\right)\) theo cmt \(\Rightarrow CD\perp HE\)
\(\Rightarrow HE\perp\left(SCD\right)\Rightarrow HE=d\left(H;\left(SCD\right)\right)\)
Hệ thức lượng:
\(\dfrac{1}{HE^2}=\dfrac{1}{SH^2}+\dfrac{1}{HK^2}\Rightarrow HE=\dfrac{a}{2}\)
Đúng 1
Bình luận (0)
Cho hình chóp SABCD có đáy ABCD là hình vuông cạnh a hai mặt phẳng SAB và SAD cùng vuông góc với mặt đáy gọi M lần lượt là trung điểm của AD tính khoảng cách giữa hai đường thẳng AB và SM biết SC = a căn 3
\(\left\{{}\begin{matrix}\left(SAB\right)\cap\left(SAD\right)=SA\\\left(SAB\right)\perp\left(ABCD\right)\\\left(SAD\right)\perp\left(ABCD\right)\end{matrix}\right.\) \(\Rightarrow SA\perp\left(ABCD\right)\)
Gọi N là trung điểm BC \(\Rightarrow MN||AB\Rightarrow AB||\left(SMN\right)\)
\(\Rightarrow d\left(AB;SM\right)=d\left(AB;\left(SMN\right)\right)=d\left(A;\left(SMN\right)\right)\)
Từ A kẻ \(AH\perp SM\)
\(\left\{{}\begin{matrix}MN||AB\Rightarrow MN\perp AD\\SA\perp\left(ABCD\right)\Rightarrow SA\perp MN\end{matrix}\right.\) \(\Rightarrow MN\perp\left(SAD\right)\Rightarrow MN\perp AH\)
\(\Rightarrow AH\perp\left(SMN\right)\Rightarrow AH=d\left(A;\left(SMN\right)\right)\)
\(AC=a\sqrt{2}\Rightarrow SA=\sqrt{SC^2-AC^2}=a\)
\(AM=\dfrac{AD}{2}=\dfrac{a}{2}\)
Áp dụng hệ thức lượng:
\(\dfrac{1}{AH^2}=\dfrac{1}{SA^2}+\dfrac{1}{AM^2}\Rightarrow AH=\dfrac{SA.AM}{\sqrt{SA^2+AM^2}}=\dfrac{a\sqrt{5}}{5}\)
Đúng 3
Bình luận (0)
Cho hình chóp SABCD. ABCD là hình vuông cạnh a, tam giác SAD đều, (SAD) vuông góc với đáy. I,J là trung điểm của AD và BC. Tính khoảng cách từ a)AD đến SB b)SA đến BD
cho hình chóp SABCD đáy là hình thang vuông tại A,B. AB=BC=a,AD=2a. Tam giác SAD đều. (SAD) vuông góc với (ABCD). Tính thể tích SABCD
Hình chóp SABCD. đay là hình vuông ABCD cạnh a. mặt phẳng (SAD) là tam giác đều và nằm trong mặt phẳng vuông góc với đáy ABCD. Goi M, N, P .lần lượt là trung điểm của SB, BC, CD. Tính thể tích khối chóp CMNP
Gọi I là trung điểm AD \(\Rightarrow SI\perp AD\Rightarrow SI\left(ABCD\right)\Rightarrow d\left(I;\left(ABCD\right)\right)=SI\)
Ta có \(SM\cap\left(ABCD\right)=\left\{B\right\}\) và \(\frac{SB}{MB}=2\) nên \(d\left(M;\left(ABCD\right)\right)=\frac{1}{2}d\left(I;\left(ABCD\right)\right)=\frac{1}{2}SI=\frac{1}{2}\cdot\frac{a\sqrt{3}}{2}=\frac{a\sqrt{3}}{4}\)
\(S_{CNP}=\frac{1}{2}\cdot CN\cdot CP=\frac{1}{2}\cdot\frac{1}{2}CD\cdot\frac{1}{2}\cdot BC=\frac{a^2}{8}\)
\(V_{M.CNP}=\frac{1}{3}\cdot d\left(M;\left(ABCD\right)\right)\cdot S_{CNP}=\frac{a^3\sqrt{3}}{96}\)
Đúng 0
Bình luận (1)
Cho hình chóp S.ABCD đáy ABCD là hình bình hành AB a, AC
a
2
,
B
C
a
3
2
,
∆
SAD vuông cân tại S và (SAD)
⊥
(ABCD). Tính thể tích V của SABCD. A. V
a
3
16
B. V
a...
Đọc tiếp
Cho hình chóp S.ABCD đáy ABCD là hình bình hành AB = a, AC = a 2 , B C = a 3 2 , ∆ SAD vuông cân tại S và (SAD) ⊥ (ABCD). Tính thể tích V của SABCD.
A. V = a 3 16
B. V = a 3 3 24
C. V = a 3 6 2
D. V = a 3 6 6
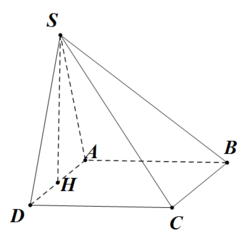
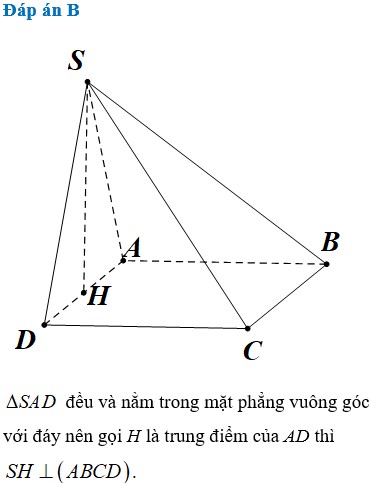
Cho hình chóp SABCD có đáy ABCD là hình vuông cạnh a, tam giác SAD đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính thể tích V của khối chóp SABCD.
Đọc tiếp
Cho hình chóp SABCD có đáy ABCD là hình vuông cạnh a, tam giác SAD đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính thể tích V của khối chóp SABCD.
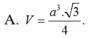
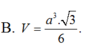
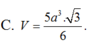
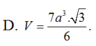
Cho hình chóp SABCD có đáy ABCD là hình vuông cạnh a, tam giác SAD đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính thể tích V của khối chóp SABCD A.
V
a
3
3
4
B.
V
a
3
3
6
C.
V...
Đọc tiếp
Cho hình chóp SABCD có đáy ABCD là hình vuông cạnh a, tam giác SAD đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính thể tích V của khối chóp SABCD
A. V = a 3 3 4
B. V = a 3 3 6
C. V = 5 a 3 3 6
D. V = 7 a 3 3 6
SABCD có ABCD là hình vuông cạnh bằng 2 , tam giác SAB đều , H là trung điểm AB
1, BC⊥ ( SAB)
2, SH ⊥ ( ABCD)
3, ((SBC);(ABCD))
4, ((SAD);(ABCD))
5,((SCD);(ABCD))
1: BC vuông góc AB
BC vuông góc SA
=>BC vuông góc (SAB)
2: ΔSAB đều
mà SH là trung tuyến
nên SH vuông góc AB
=>SH vuông góc (ABCD)
Đúng 1
Bình luận (0)