Cho hai đường thẳng (d1)y=mx+2m và (d2)y=(2m−3)x+2. Để (d1)⊥(d2) thì m bằng :

Những câu hỏi liên quan
Cho đường thẳng d 1 :y = mx + 2m - 1 (với m là tham số) và d 2 : y = x + 1
a) Với m = 2. Hãy vẽ các đường thẳng d 1 và d 2 trên cùng một mặt phẳng tọa độ. Tìm tọa độ gia điểm của hai đường thẳng d 1 và d 2
Với m = 2 thì d 1 : y = 2x + 3; d 2 : y = x + 1
Tập xác định của hàm số R
Bảng giá trị
| x | 0 | - 1 |
| y = 2x + 3 | 3 | 1 |
| x | 0 | - 1 |
| y = x + 1 | 1 | 0 |
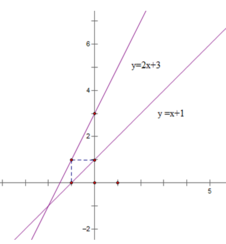
Gọi A ( x 0 ; y 0 ) là tọa độ giao điểm của d1 và d2
Khi đó:
( y 0 = 2 x 0 + 3 và y 0 = x 0 + 1
⇒ 2xo + 3 = x 0 + 1 ⇔ x 0 = -2
⇒ y 0 = x 0 + 1 = -2 + 1 = -1
Vậy tọa độ giao điểm của d 1 và d 2 là (-2; -1)
Đúng 0
Bình luận (0)
Bài 1: Cho hai đường thẳng (d1):y = -2x + 1 và (d2):y = (2m - 3)x + 3 - m. Tìm m để (d1) cắt (d2) tại điểm có tung độ bằng 3.
Do giao điểm có tung độ bằng 3 nên hoành độ thỏa mãn:
\(3=-2x+1\Rightarrow x=-1\)
Thế tọa độ giao điểm vào pt d2 ta được:
\(3=-\left(2m-3\right)+3-m\)
\(\Rightarrow-3m+3=0\Rightarrow m=1\)
Đúng 4
Bình luận (0)
cho hai đường thẳng (d1) y=(2+m)x+1 và (d2) y=(1+2m)x+2
1)tìm m để (d1) và (d2) cắt nhau
2)với m=-1 vẽ d1 và d2 trên cùng mặt phẳng tọa độ Oxy rôi tìm tọa độ giao điểm của 2 đường thẳng d1 và d2 bằng phép tính
Ai giúp mình với ạ
thank nhiều
1: Để hai đường thẳng cắt nhau thì
2m+1<>m+2
hay m<>1
Đúng 0
Bình luận (0)
Cho ba đường thẳng
d
1
:
x
−
2
y
+
1
0
,
d
2
:
m
x
−
3
m
−
2
y
+
2
m
−
2
0
,
d
3
:
...
Đọc tiếp
Cho ba đường thẳng d 1 : x − 2 y + 1 = 0 , d 2 : m x − 3 m − 2 y + 2 m − 2 = 0 , d 3 : x + y − 5 = 0 . Giá trị m để hai đường thẳng d1;d2 cắt nhau tại một điểm nằm trên d3 là
A.m = 0
B.m = 1
C.m = 2
D. không tồn tại m thỏa mãn
Để hai đường thẳng d1; d2 cắt nhau tại một điểm nằm trên d3 khi và chỉ khi 3 đường thẳng d1; d2; d3 đồng quy.
Giao điểm của d1 và d3 là nghiệm hệ phương trình:
x − 2 y + 1 = 0 x + y − 5 = 0 ⇔ x = 3 y = 2 ⇒ A ( 3 ; 2 )
Do 3 đường thẳng này đồng quy nên điểm A thuộc d2. Suy ra:
3m - (3m-2).2 + 2m – 2= 0
⇔ 3m – 6m + 4 + 2m – 2 = 0 ⇔ - m + 2 = 0 ⇔ m= 2
Với m= 2 thì đường thẳng d2 : 2x - 4y + 2= 0 hay x- 2y + 1 =0 . Khi đó, đường thẳng d1 và d2 trùng nhau.
Vậy không có giá trị nào của m thỏa mãn.
ĐÁP ÁN D
Đúng 0
Bình luận (0)
Cho đường thẳng d 1 :y = mx + 2m - 1 (với m là tham số) và d 2 : y = x + 1
b) Tìm giá trị của m để đường thẳng d 1 cắt trục hoành tại điểm có hoành độ bằng – 3.
b) d 1 cắt trục hoành tại điểm có hoành độ bằng – 3 khi:
0 = -3m + 2m - 1 ⇔ -m - 1 = 0 ⇔ m = -1
Vậy với m = -1 thì d 1 cắt trục hoành tại điểm có hoành độ bằng – 3
Đúng 0
Bình luận (0)
Cho hai đường thẳng (d1):y = -2x + 1 và (d2):y = (2m - 3)x + 3 - m. Tìm m để (d1) cắt (d2) tại điểm có tung độ bằng 3. Giá trị của m là:...
Bài 1:Xác định m để ba đường thẳng sau: 1: y -2x, d2: y -x +1, d3 : y -(m +3)x - 2m +1 đồng quy.Bài 2: Trên cùng một mặt phẳng tọa độ cho hàm số d1 : y -2x và d2 : y x+3. a) Tìm tọa độ giao điểm của hai đường thẳng d1 và d2 bằng hai cách.b) Viết phương trình đường thẳng d3 biết đường thẳng này song song với d1 và cắt d2 tại điểm có hoành độ bằng 1.Bài 3 :Xác định các hệ số a, b biết đường thẳng d: y ax +b song song với đường thẳng d1 : y 3.x và cắt trục hoành tại điểm có hoành độ bằng 2/3
Đọc tiếp
Bài 1:Xác định m để ba đường thẳng sau:
1: y= -2x, d2: y = -x +1, d3 : y = -(m +3)x - 2m +1 đồng quy.
Bài 2: Trên cùng một mặt phẳng tọa độ cho hàm số d1 : y = -2x và d2 : y = x+3. a) Tìm tọa độ giao điểm của hai đường thẳng d1 và d2 bằng hai cách.
b) Viết phương trình đường thẳng d3 biết đường thẳng này song song với d1 và cắt d2 tại điểm có hoành độ bằng 1.
Bài 3 :Xác định các hệ số a, b biết đường thẳng d: y ax +b song song với đường thẳng d1 : y = 3.x và cắt trục hoành tại điểm có hoành độ bằng 2/3
Bài 3:
Vì (d)//(d1) nên a=3
Vậy: (d): y=3x+b
Thay \(x=\dfrac{2}{3}\) và y=0 vào (d), ta được:
\(b+2=0\)
hay b=-2
Đúng 0
Bình luận (1)
Cho hai đường thẳng
\(d1:y=mx-2\left(m+2\right)vớim\ne0\)
\(d2:y=\left(2m-3\right)x+\left(m^2-1\right)vớim\ne\frac{3}{2}\)
CMR: với mọi gtri của m, hai đt d1 và d2 không trùng nhau
tìm các gtr m để d1//d2, d1 cắt d2, d1 vuông góc với d2
a) Giả sử d1 trùng d2 => có m để
=>\(\int^{2m-3=m}_{m^2-1=-2m-4}\Leftrightarrow\int^{m=3}_{m^2+2m+3=0\left(vônghiem\right)}\)
=> d1 khong trùng với d2
b)
+d1//d2 => m=3
+d1 cắt d2 => m\(\ne\)3
+d1 vuông góc d2 => m(2m-3) =-1 => 2m2 -3m +1 =0 => m =1 ; m = 1/2
Đúng 0
Bình luận (0)
Cho 2 đường thẳng (d1):
y = m(x+2);(d2):y=(2m-3)x+2 Tìm m để:
a) (d1) và (d2) song song với nhau.
b) (d1) và (d2) trùng với nhau.
c) (d1) và (d2) vuông góc với nhau.
a) \(\left(d_1\right):y=mx+2m\)
\((d_1)\parallel (d_2)\) \(\Rightarrow\left\{{}\begin{matrix}m=2m-3\\2m\ne2\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}m=3\\m\ne1\end{matrix}\right.\Rightarrow m=3\)
b) \(\left(d_1\right)\equiv\left(d_2\right)\Rightarrow\left\{{}\begin{matrix}m=2m-3\\2m=2\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}m=3\\m=1\end{matrix}\right.\Rightarrow\) không có m thỏa
c) \(\left(d_1\right)\bot\left(d_2\right)\Rightarrow m.\left(2m-3\right)=-1\Rightarrow2m^2-3m+1=0\)
\(\Rightarrow\left(m-1\right)\left(2m-1\right)=0\Rightarrow\left[{}\begin{matrix}m=1\\m=\dfrac{1}{2}\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Ta có: (d1): y=m(x+2)
nên y=mx+2m
a) Để (d1)//(d2) thì \(\left\{{}\begin{matrix}m=2m-3\\2m\ne2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m-2m=-3\\m\ne1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=3\\m\ne1\end{matrix}\right.\Leftrightarrow m=3\)
Đúng 0
Bình luận (0)
b) Để (d1) trùng với (d2) thì \(\left\{{}\begin{matrix}m=2m-3\\2m=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=3\\m=1\end{matrix}\right.\Leftrightarrow m\in\varnothing\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời















