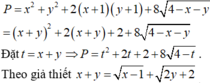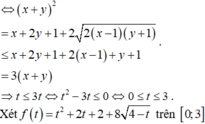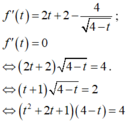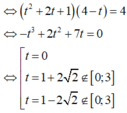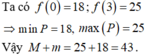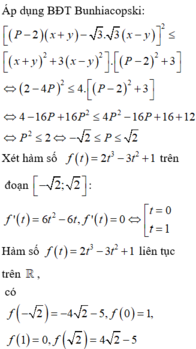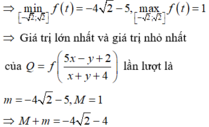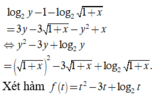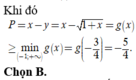Cho các số thực x, y thỏa mãn x2 + y2 = 1. Giá trị nhỏ nhất của S = x + y bằng:

Những câu hỏi liên quan
Cho các số thực x, y thỏa mãn x2 + y2 = 8. Giá trị nhỏ nhất của S = x + y bằng:
\(\left(x+y\right)^2\le2\left(x^2+y^2\right)=16\)
\(\Rightarrow x+y\ge-4\)
\(S_{min}=-4\)
Đúng 0
Bình luận (0)
Cho x , y là các số thực thỏa mãn
x
+
y
x
-
1
+
2
y
+
2
. Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của
P
x
2...
Đọc tiếp
Cho x , y là các số thực thỏa mãn x + y = x - 1 + 2 y + 2 . Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của P = x 2 + y 2 + 2 ( x + 1 ) ( y + 1 ) + 8 4 - x - y . Khi đó, giá trị của M+m bằng.
A. 41
B. 42
C. 43
D. 44
Cho x, y là các số thực dương thỏa mãn x2+ y2=1. Tìm giá trị nhỏ nhất của biểu thức:
P= x + \(\dfrac{1}{x}\) + y + \(\dfrac{1}{y}\)
Điểm rơi: \(x=y=\frac{\sqrt{2}}{2}\)
Ta tách biểu thức được như sau: \(A=x+\frac{1}{x}+y+\frac{1}{y}=(x+\frac{1}{2x})+(y+\frac{1}{2y})+\frac{1}{2}(\frac{1}{2x}+\frac{1}{2y})\)
\(\geq 2\sqrt{x.\frac{1}{2x}}+2\sqrt{y.\frac{1}{2y}}+\frac{1}{2}.\frac{4}{x+y}=2\sqrt{2}+\frac{2}{x+y}\)
Áp dụng bất đẳng thức Bunhiacốpxki, ta lại có:
\((x+y)^2\leq 2(x^2+y^2)=2 \Rightarrow x+y\leq \sqrt{2}\)
\(\Rightarrow A\geq 3\sqrt{2}\)
Dấu bằng xảy ra khi \(x=y=\frac{\sqrt{2}}{2}\)
Đúng 1
Bình luận (0)
đây là những món quà mà bn sẽ nhận đc: 1: áo quần 2: tiền 3: đc nhiều người yêu quý 4: may mắn cả 5: luôn vui vẻ trong cuộc sống 6: đc crush thích thầm 7: học giỏi 8: trở nên xinh đẹp phật sẽ ban cho bn những điều này nếu cậu gửi tin nhắn này cho 25 người,
Đúng 0
Bình luận (0)
Cho x, y là các số thực thỏa mãn
x
+
y
x
-
1
+
2
y
+
2
Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của
P
x
2
+
y
2
+
2
(
x
+
1
)
(
y
+
1
)
+
8
4
-
x
-...
Đọc tiếp
Cho x, y là các số thực thỏa mãn x + y = x - 1 + 2 y + 2 Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của P = x 2 + y 2 + 2 ( x + 1 ) ( y + 1 ) + 8 4 - x - y Tính giá trị M + m
A. 41
B. 44
C. 42
D. 43
Cho các số thực x, y thay đổi thỏa mãn
x
2
+
y
2
-
x
y
1
và hàm số
f
t
2
t
3
-
3
t
2
-
1
. Gọi M, m tương ứng là giá trị lớn nhất và giá trị nhỏ nhất của
Q
f...
Đọc tiếp
Cho các số thực x, y thay đổi thỏa mãn x 2 + y 2 - x y = 1 và hàm số f t = 2 t 3 - 3 t 2 - 1 . Gọi M, m tương ứng là giá trị lớn nhất và giá trị nhỏ nhất của Q = f 5 x - y + 2 x + y + 4 . Tổng M + m bằng
A. - 4 - 3 2
B. - 4 - 5 2
C. - 4 - 4 2
D. - 4 - 2 2
Cho 2 số thực x ; y thỏa mãn 0 < x ≤ 1 , 0 < y ≤ 1 và x + y = 3xy . Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P = x2 + y2 - 4xy
Cho x , y là các số thực dương thỏa mãn x + y + xy = 8 . Tìm giá trị nhỏ nhất của biểu thức A = x2 + y2
Cho x, y là các số thực thỏa mãn
log
2
y
2
1
+
x
3
y
-
1
+
x
-
y
2
+
x
. Giá trị nhỏ nhất của biểu thức
P
x...
Đọc tiếp
Cho x, y là các số thực thỏa mãn log 2 y 2 1 + x = 3 y - 1 + x - y 2 + x . Giá trị nhỏ nhất của biểu thức P = x - y bằng
A. - 3 4
B. - 5 4
C. -2
D. -1
Cho x, y là các số thực thỏa mãn điều kiện x2 + y2= 1 .Tìm giá trị nhỏ nhất của biểu thức P = (3-x) χ (3-y)
( có thể dùng BĐT Bunhia copxki)
Do \(x^2+y^2=1\), đặt \(\left\{{}\begin{matrix}x=sina\\y=cosa\end{matrix}\right.\)
\(P=\left(3-sina\right)\left(3-cosa\right)=9-3\left(sina+cosa\right)+sina.cosa\)
Đặt \(sina+cosa=t\Rightarrow t\in\left[-\sqrt{2};\sqrt{2}\right]\)
\(t^2=1+2sina.cosa\Rightarrow sina.cosa=\dfrac{t^2-1}{2}\)
\(P=9-3t+\dfrac{t^2-1}{2}=\dfrac{1}{2}t^2-3t+\dfrac{17}{2}\)
Xét hàm \(f\left(t\right)=\dfrac{1}{2}t^2-3t+\dfrac{17}{2}\) trên \(\left[-\sqrt{2};\sqrt{2}\right]\)
\(f'\left(t\right)=t-3=0\Rightarrow t=3\notin\left[-\sqrt{2};\sqrt{2}\right]\)
\(f\left(-\sqrt{2}\right)=\dfrac{19+6\sqrt{2}}{2}\) ; \(f\left(\sqrt{2}\right)=\dfrac{19-6\sqrt{2}}{2}\)
\(\Rightarrow P_{min}=f\left(\sqrt{2}\right)=\dfrac{19-6\sqrt{2}}{2}\) khi \(t=\sqrt{2}\)
Đúng 1
Bình luận (0)