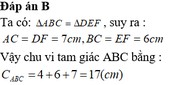cho tam giác abc=tam giác def có ab=3cm,df=4cm,ef=5cm.tính chu vi của mỗi tam giác

Những câu hỏi liên quan
Bài 1:Cho tam giác ABC có A80 độ,B40 độ.Tia phân giác của góc C cắt AB tại D.Tính số đo góc CDA;CDB.Bài 2:Cho tam giác ABCtam giác DEF có AB3cm,DF 4cm,EF5cm.Tính chu vi của mỗi tam giác.Bài 3:Cho tam giác ABC có ABAC,D là trung điểm của BC(D thuộc BC).Chứng minh:a)Tam giác ABD tam giác ACD b)BADCAD c)AD vuông góc BCLƯU Ý:NHỮNG BÀI TRÊN KO CÓ BÀI NÀO CÓ HÌNH CẢ
Đọc tiếp
Bài 1:Cho tam giác ABC có A=80 độ,B=40 độ.Tia phân giác của góc C cắt AB tại D.Tính số đo góc CDA;CDB.
Bài 2:Cho tam giác ABC=tam giác DEF có AB=3cm,DF= 4cm,EF=5cm.Tính chu vi của mỗi tam giác.
Bài 3:Cho tam giác ABC có AB=AC,D là trung điểm của BC(D thuộc BC).Chứng minh:
a)Tam giác ABD= tam giác ACD b)BAD=CAD c)AD vuông góc BC
LƯU Ý:NHỮNG BÀI TRÊN KO CÓ BÀI NÀO CÓ HÌNH CẢ
Bài 3:
a: Xét ΔABD và ΔACD có
AB=AC
AD chung
BD=CD
Do đó: ΔABD=ΔACD
b: Ta có: ΔABD=ΔACD
nên \(\widehat{BAD}=\widehat{CAD}\)
c: Ta có: ΔABC cân tại A
mà AD là đường trung tuyến
nên AD là đường cao
Đúng 0
Bình luận (0)
Cho tam giác abc = tam giác def có AB= 3cm,DF= 4cm,EF=5cm. Tính chu vi mỗi tam giác ? mn giúp mình với
\(C_{ABC}=C_{DEF}=12\left(cm\right)\)
Đúng 0
Bình luận (0)
Cho tam giác ABC = tâm giác DEF . Biết AB=3cm , AC=4cm , EF=5cm. Tính chu vi của mỗi tam giác.
\(C_{ABC}=C_{DEF}=12\left(cm\right)\)
Đúng 0
Bình luận (0)
Xét tam giác ABC:
BC=EF=5cm
=> Chu vi của tam giác ABC là:
AB+AC+BC=3+4+5=12(cm)
Xét tam giác DEF:
AB=DE=3cm
AC=DF=4cm
=> Chu vi tam giác DEF là:
DE+DF+EF=3+4+5=12
Vậy chu vi tam giác ABC: 12(cm)
Chu vi tam giác DEF:12(cm)
Đúng 1
Bình luận (0)
Cho tam giác ABC bằng tam giác DEF biết AB=3cm AC=4cm EF=6cm tính chu vi tam giác nói trên
Cho tam giác ABC= tam giác DEF biết AB=3cm Ac=4cm EF=6cm tính chu vi tam giác nói trên
Vì tam giác ABC = tam giác DEF => AB = DE,BC =EF, AC = DF. Vậy chu vi của tam giác DEF = 3+4+6 =13cm.
Đúng 0
Bình luận (0)
Ta có:tam giác ABC = tam giác DEF (gt)
\(\Rightarrow\)AB = DE
AC = DF
BC = EF
Mà theo đề ta có : AB = 3cm \(\rightarrow\) DE =3cm ; AC = 4cm \(\rightarrow\)DF =4cm ; EF = 6cm\(\rightarrow\)BC = 6cm
nên ta có chu vi của tam giác ABC là:
AB + AC + BC = 3 + 4 + 6 = 13 (cm)
Vì tam giác ABC = tam giác DEF
Do đó: tam giác DEF có chu vi là : 13 (cm)
Đúng 0
Bình luận (0)
Cho △ A B C = △ D E F
Biết AB = 4cm; EF = 6cm; DF = 7cm. Tính chu vi tam giác ABC
A. 15 cm
B. 17 cm
C. 16 cm
D. 8,5 cm
cho tam giác DEF đồng dạng với tam giác ABC .tính các cạnh của tam giác ABC biết DE=3cm,DF=5cm,EF=7cm và chu vi tam giác ABC =20cm
Ai bt ko giúp mình với
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AB}{3}=\dfrac{AC}{5}=\dfrac{BC}{7}=\dfrac{AB+BC+CA}{3+5+7}=\dfrac{20}{15}=\dfrac{4}{3}\)
Do đó: AB=4(cm); AC=20/3(cm); BC=28/3(cm)
Đúng 0
Bình luận (0)
ta có:\(\dfrac{DE}{AB}=\dfrac{DF}{AC}=\dfrac{EF}{BC}\)
\(\Leftrightarrow\dfrac{3}{AB}=\dfrac{5}{AC}=\dfrac{7}{BC}\)
áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\dfrac{3+5+7}{AB+AC+BC}=\dfrac{15}{20}=\dfrac{3}{4}\)
<=>\(\dfrac{AB+AC+BC}{DE+EF+DF}=\dfrac{4}{3}\)
<=>AB=\(\dfrac{4}{3}.DE=\dfrac{4}{3}.3=4\)
AC=\(\dfrac{4}{3}.DF=\dfrac{4}{3}.5=\dfrac{20}{3}\)
BC=\(\dfrac{4}{3}.EF=\dfrac{4}{3}.7=\dfrac{28}{3}\)
VẬY...
Đúng 1
Bình luận (0)
cho tam giác ABC =tam giác DEF biết ab=4cm , AC=6cm,EF=5cm
tính chu vi mỗi tam giác trên
ΔABC=DEFΔABC=DEF
=> AB=DE=3cm; BC=EF=5cm; AC=DF=4cm.
Diện tích ΔABCΔABC=Diện tích ΔDEFΔDEF=3+5+4=12 (cm)
Đ/S:12
ai k mik 3 cái mik k lại 9 cái
#mai