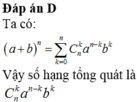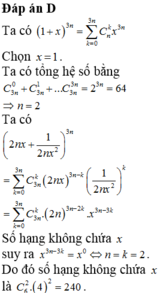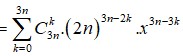Các câu khai triển giải bằng công thức số hạng tổng quát giúp em ạ

Những câu hỏi liên quan
Câu 123 giải giúp em bằng công thức số hạng tổng quát ạ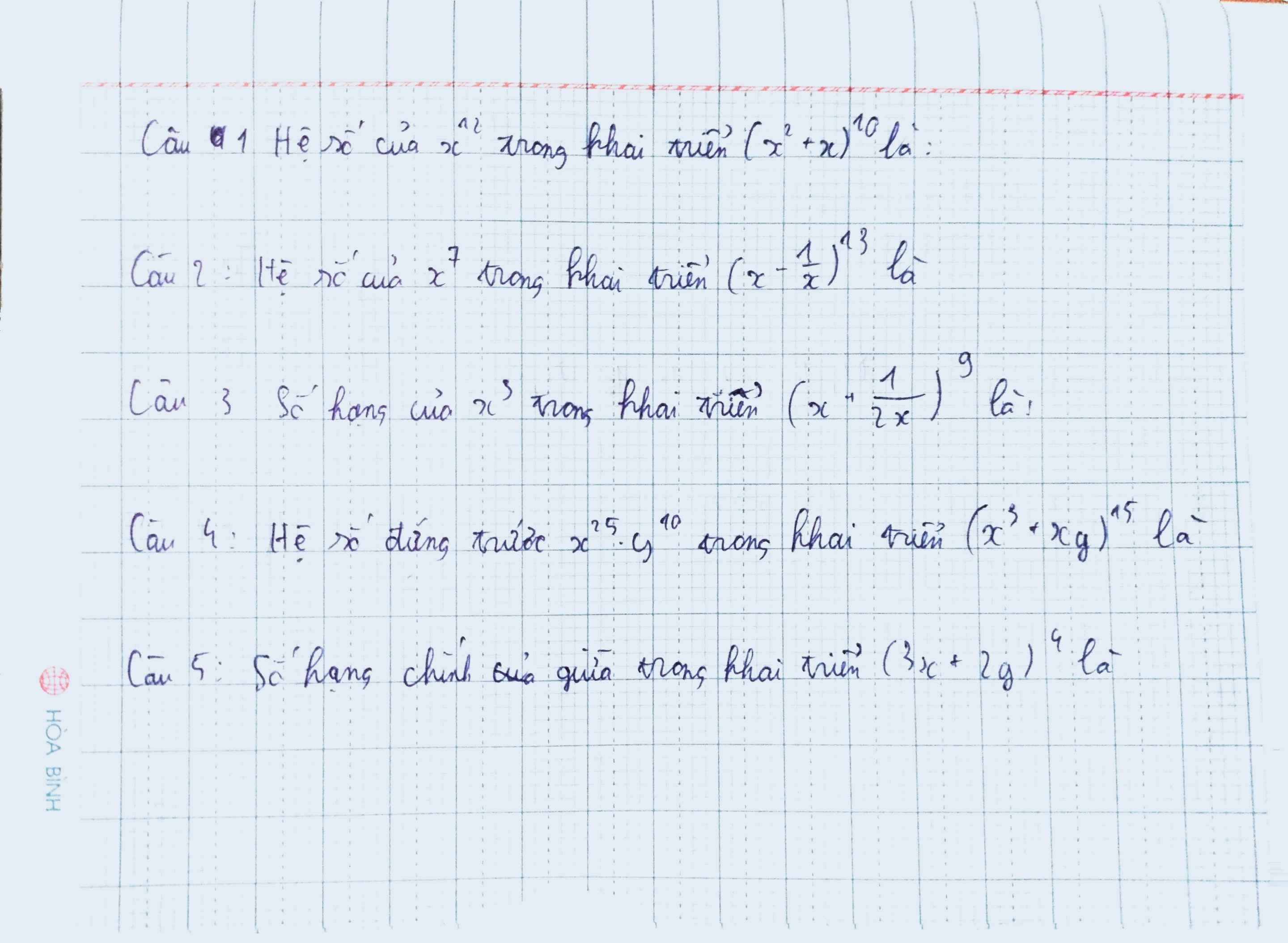
1.
\(\left(x^2+x\right)^{10}=\sum\limits^{10}_{k=0}C^k_{10}.\left(x^2\right)^{10-k}.x^k=\sum\limits^{10}_{k=0}C^k_{10}.x^{20-k}\)
\(\Rightarrow20-k=12\Rightarrow k=8\)
\(\Rightarrow\) Hệ số của \(x^{12}\) trong khai triển \(\left(x^2+x\right)^{10}\) là: \(C^8_{10}=45\)
Đúng 1
Bình luận (0)
2.
\(\left(x-\dfrac{1}{x}\right)^{13}=\sum\limits^{13}_{k=0}C^k_{13}.x^{13-k}.\dfrac{1}{x^k}=\sum\limits^{13}_{k=0}C^k_{13}.x^{13-2k}\)
\(\Rightarrow13-2k=7\Rightarrow k=3\)
\(\Rightarrow\) Hệ số của \(x^7\) trong khai triển \(\left(x-\dfrac{1}{x}\right)^{13}\) là: \(C^3_{13}=286\)
Đúng 1
Bình luận (0)
3.
\(\left(x+\dfrac{1}{2x}\right)^9=\sum\limits^9_{k=0}C^k_9.x^{9-k}.\dfrac{1}{2^k.x^k}=\sum\limits^9_{k=0}\dfrac{C^k_9}{2^k}.x^{9-2k}\)
\(\Rightarrow9-2k=3\Rightarrow k=3\)
\(\Rightarrow\) Hệ số của \(x^3\) trong khai triển \(\left(x+\dfrac{1}{2x}\right)^9\) là: \(\dfrac{C^3_9}{2^3}=\dfrac{21}{2}\)
Đúng 1
Bình luận (1)
Xem thêm câu trả lời
Tìm hệ số của số hạng chứa x trong khai triển (2+3x) mũ 5 ( sử dụng công thức tổng quát Nhị Thức Newton)
SHTQ của \(\left(3x+2\right)^5\) là \(C^k_5\cdot\left(3x\right)^{5-k}\cdot2^k=C^k_5\cdot3^{5-k}\cdot2^k\cdot x^{5-k}\)
Hệ số của số hạng chứa x tương ứng với 5-k=1
=>k=4
=>Hệ số là \(C^4_5\cdot3^{5-4}\cdot2^4=240\)
Đúng 1
Bình luận (0)
Trong khai triển
a
+
b
n
,
số hạng tổng quát của khai triển là: A.
C
n
k
+
1
a
n
−
k
+
1
b...
Đọc tiếp
Trong khai triển a + b n , số hạng tổng quát của khai triển là:
A. C n k + 1 a n − k + 1 b k + 1
B. C n k + 1 a k + 1 b n − k + 1
C. C n k + 1 a n − k b n − k
D. C n k + 1 a n − k b k
Đáp án D
Ta có: a + b n = ∑ k = 0 n C n k a n − k b k ⇒ số hạng tổng quát là C n k a n − k b k
Đúng 0
Bình luận (0)
Trong khai triển
a
+
b
n
, số hạng tổng quát của khai triển là
Đọc tiếp
Trong khai triển a + b n , số hạng tổng quát của khai triển là
![]()
![]()
![]()
![]()
Biết tổng hệ số của ba số hạng đầu tiên trong khai triển
(
x
3
-
2
x
)
n
theo công thức nhị thức Niu-tơn bằng 161. Hệ số của số hạng chứa
x
2
bằng A. 13440. B. -15360. C. 15360. D.-13440
Đọc tiếp
Biết tổng hệ số của ba số hạng đầu tiên trong khai triển ( x 3 - 2 x ) n theo công thức nhị thức Niu-tơn bằng 161. Hệ số của số hạng chứa x 2 bằng
A. 13440.
B. -15360.
C. 15360.
D.-13440
Tìm số hạng tổng quát trong khai triển
a
+
b
n
A.
C
n
k
a
k
+
1
b
k
B.
C
n...
Đọc tiếp
Tìm số hạng tổng quát trong khai triển a + b n
A. C n k a k + 1 b k
B. C n k a k b k
C. C n k + 1 a n - k b k
D. C n k a n - k b k
Tổng các hệ số nhị thức Niu – tơn trong khai triển
1
+
x
3
n
bằng 64. Số hạng không chứa x trong khai triển
2
n
x
+
1
2
n
x...
Đọc tiếp
Tổng các hệ số nhị thức Niu – tơn trong khai triển 1 + x 3 n bằng 64. Số hạng không chứa x trong khai triển 2 n x + 1 2 n x 2 3 n là
A. 360
B. 210
C. 250
D. 240
Tổng các hệ số nhị thức Niu – tơn trong khai triển (1+x)3n bằng 64. Số hạng không chứa x trong khai triển
2
n
x
+
1
2
n
x
2
3...
Đọc tiếp
Tổng các hệ số nhị thức Niu – tơn trong khai triển (1+x)3n bằng 64. Số hạng không chứa x trong khai triển 2 n x + 1 2 n x 2 3 n là:
A. 360
B. 210
C. 250
D. 240
Ta có: 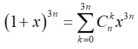
Chọn x=1. Ta có tổng hệ số bằng: ![]()
Lại có: 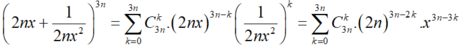
Số hạng không chứa x suy ra ![]()
Do đó số hạng không chứa x là: ![]()
Chọn D.
Đúng 0
Bình luận (0)
Tổng các hệ số nhị thức Niu – tơn trong khai triển
(
1
+
x
)
3
n
bằng 64. Số hạng không chứa x trong khai triển
(
2
n
x
+
1
2
n...
Đọc tiếp
Tổng các hệ số nhị thức Niu – tơn trong khai triển ( 1 + x ) 3 n bằng 64. Số hạng không chứa x trong khai triển ( 2 n x + 1 2 n x 2 ) 3 n là
A. 360
B. 210
C. 250
D. 240