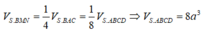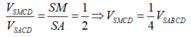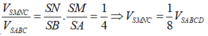Cho hình chóp S.ABCD có M,N lần lượt là trung điểm của SA, AC; P thuộc AB sao cho 2PB = AB, I thuộc SC sao cho SC= 3SI. Tìm giao điểm a. SI và (MNP) b. AC và (MNP) c. SB và (MNP) Giúp e chi tiết bài này vs ạ^^

Những câu hỏi liên quan
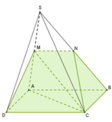
cho hình chóp s.abcd có ABCD là hình bình hành. M,N,P,Q lần lượt là trung điểm của SA,SB,SC,SD. Tí số thể tích của khối chóp S.MNPQ và khối chóp S.ABCD
Theo công thức Simsons ta có:
\(\dfrac{V_{SMNPQ}}{V_{SABCD}}=\dfrac{2V_{SMNP}}{2V_{SABC}}=\dfrac{SM}{SA}.\dfrac{SN}{SB}.\dfrac{SP}{SC}=\dfrac{1}{2}.\dfrac{1}{2}.\dfrac{1}{2}=\dfrac{1}{8}\)
Đúng 2
Bình luận (1)
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của SA, SC. Biết thể tích của khối chóp S.BMN là
a
3
. Tính thể tích khối chóp S.ABCD A.
a
3
B. 4
a
3
C. 8
a
3
D. 16
a
3
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của SA, SC. Biết thể tích của khối chóp S.BMN là a 3 . Tính thể tích khối chóp S.ABCD
A. a 3
B. 4 a 3
C. 8 a 3
D. 16 a 3
Cho hình chóp S.ABCD có đáy là hình. Gọi M, N, P lần lượt là trung điểm của AD BC SA. Tìm thiết diện của hình chóp vs mp(MNP)
Đáy là hình gì bạn?
Mỗi dữ liệu quan trọng thì lại không có :(
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
cho hình chóp s.abcd đáy abcd là hình thang AD//BC, O là giao điểm của ac và bd gọi M,N lần lượt là trung điểm SA,SD.xác định thiết diện hình chóp cắt bởi mặt phẳng omn
Bài 1: cho hình chóp S.ABCD có đáy ABCD là hình thang , BAD=ABC= 90 độ. Cạnh AB=BC=a, AD=2a, SA vuông góc ( ABCD ), Sa=2a. Gọi M,N lần lượt là trung điểm của SA và SD. Tính theo a thể tích khối chóp S.BCNM
Bài 2: cho hình chóp tứ giác đều S.ABCD có AB = a; SA = a\(\sqrt{2}\) . Gọi M,N lần lượt là trung điểm của SA,SB,SD. Tính theo a thể tích của khối tứ diện A.MNP
Cho khối chóp S.ABCD có đáy là hình vuông. Gọi M, N lần lượt là trung điểm của SA, SB. Tính tỉ số
V
N
B
C
M
A
D
V
S
.
A
B
C
D
A.
5...
Đọc tiếp
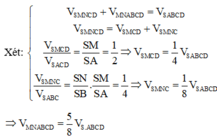
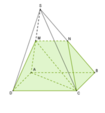
Cho khối chóp S.ABCD có đáy là hình vuông. Gọi M, N lần lượt là trung điểm của SA, SB. Tính tỉ số V N B C M A D V S . A B C D
A. 5 8 .
B. 1 2
C. 3 4
D. 5 4
Cho khối chóp S.ABCD có đáy là hình vuông. Gọi M, N lần lượt là trung điểm của SA, SB. Tính tỉ số
V
N
B
C
M
A
D
V
S
....
Đọc tiếp
Cho khối chóp S.ABCD có đáy là hình vuông. Gọi M, N lần lượt là trung điểm của SA, SB. Tính tỉ số V N B C M A D V S . A B C D
A. 5 8
B. 1 2
C. 3 4
D. 5 4
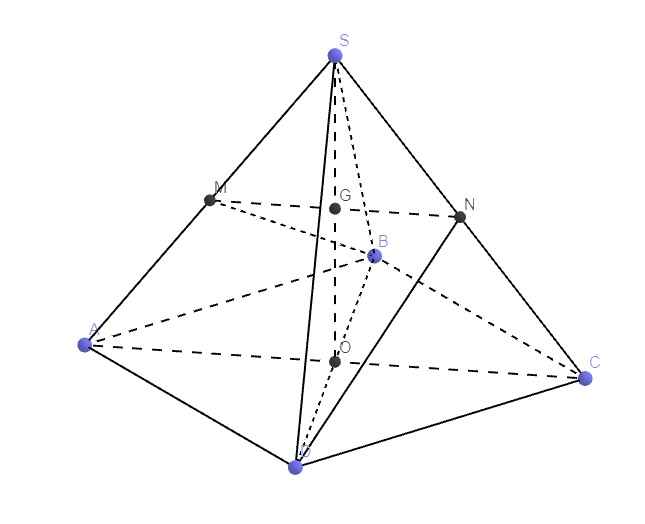
Cho hình chóp đều S.ABCD, đáy là hình vuông tâm O cạnh a. Gọi M,N lần lượt là lần lượt là trung điểm của SA,SC. Biết BM vuống góc DN. Tính thể tích hình chóp S.ABCD.
Em cảm ơn ạ !!!
Gọi O là tâm đáy và G là giao điểm của SO và MN
Do MN là đường trung bình tam giác SAC \(\Rightarrow\) G là trung điểm SO
\(\overrightarrow{BO}=\dfrac{1}{2}\overrightarrow{BD}\) ; \(\overrightarrow{OG}=\dfrac{1}{2}\overrightarrow{OS}\) ; \(\overrightarrow{GM}=\dfrac{1}{2}\overrightarrow{NM}=\dfrac{1}{4}\overrightarrow{CA}\) ; \(\overrightarrow{GN}=\dfrac{1}{2}\overrightarrow{MN}=\dfrac{1}{4}\overrightarrow{AC}\)
Ta có:
\(\left\{{}\begin{matrix}\overrightarrow{BM}=\overrightarrow{BO}+\overrightarrow{OG}+\overrightarrow{GM}\\\overrightarrow{DN}=\overrightarrow{DO}+\overrightarrow{OG}+\overrightarrow{GN}\end{matrix}\right.\)
\(\overrightarrow{BM}.\overrightarrow{CN}=0\Rightarrow\left(\overrightarrow{BO}+\overrightarrow{OG}+\overrightarrow{GM}\right)\left(\overrightarrow{CO}+\overrightarrow{OG}+\overrightarrow{GN}\right)=0\)
\(\Leftrightarrow\left(\dfrac{1}{2}\overrightarrow{BD}+\dfrac{1}{2}\overrightarrow{OS}+\dfrac{1}{4}\overrightarrow{CA}\right)\left(\dfrac{1}{2}\overrightarrow{DB}+\dfrac{1}{2}\overrightarrow{OS}+\dfrac{1}{4}\overrightarrow{AC}\right)=0\)
\(\Leftrightarrow-\dfrac{1}{4}BD^2+\dfrac{1}{4}OS^2-\dfrac{1}{4}AC^2=0\) (3 vecto \(\overrightarrow{OS};\overrightarrow{BD};\overrightarrow{CA}\) đôi một vuông góc nên tích vô hướng giữa các cặp đều bằng 0)
\(\Leftrightarrow SO^2=2AC^2\Rightarrow SO=AC\sqrt{2}=2a\)
\(V=\dfrac{1}{3}SO.AB^2=\dfrac{2}{3}a^3\)
Đúng 0
Bình luận (6)
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N lần lượt là trung điểm SA, AB. Thiết diện tạo bởi mặt phẳng (OMN) và hình chóp S.ABCD là hình gì ?
A. Hình bình hành.
B. Hình thang.
C. Hình vuông.
D. Tam giác.
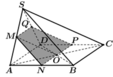
Tham khảo hình vẽ bên.
Gọi P, Q lần lượt là trung điểm của CD, SD. Khi đó thiết diện tạo bởi mặt phẳng (OMN) với hình chóp là hình thang MNPQ. Thật vậy:
![]()
Chọn B.
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD, đáy ABCD là hình chữ nhật,
A
B
S
A
a
,
A
D
a
2
,
S
A
vuông góc với đáy. Gọi M, N lần lượt là trung điểm của AD và SC, gọi I là giao điểm của BM và AC. Tỷ số
V
A
M
N
I
V...
Đọc tiếp
Cho hình chóp S.ABCD, đáy ABCD là hình chữ nhật, A B = S A = a , A D = a 2 , S A vuông góc với đáy. Gọi M, N lần lượt là trung điểm của AD và SC, gọi I là giao điểm của BM và AC. Tỷ số V A M N I V S . A B C D là?
A. 1/24
B. 1/12
C. 1/6
D.1/7
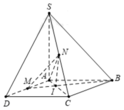
Đáp án A
Vì A M / / B C ⇒ I M I B = M A B C = 1 2 ⇒ d I ; A D d B ; A D = 1 3
|
Suy ra S Δ I M A = 1 2 d I ; A D . A M = 1 2 . 1 3 d B ; A D . 1 2 A D = S A B C D 12
Mà N là trung điểm của S C ⇒ d N ; A B C D = 1 2 d S ; A B C D
Vậy V A M N I V S . A B C D = d N ; A B C D d S ; A B C D . S Δ I M A S A B C D = 1 2 . 1 12 = 1 24
Đúng 0
Bình luận (0)