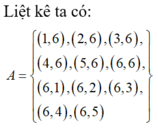Gieo con súc sắc 3 lần Tính xác suất của biến cố gieo có đúng 1 lần ra 6 chấm

Những câu hỏi liên quan
gieo một con súc sắc đồng chất cân đối ba lần liên tiếp tính xác suất của biến cố " tổng số chấm ba lần gieo không chia hết cho 5"
Khi gieo con súc sắc 1 lần xác suất để xuất hiện mặt 1 chấm là 1/6. Gieo
con súc sắc 250 lần. Tính xác suất để trong 250 lần gieo đó mặt 1 chấm xuất hiện từ 45 đến 49
lần
Gieo ngẫu nhiên một con súc sắc 3 lần liên tiếp. Gọi a,b,c lần lượt là số chấm xuất hiện ở 3 lần gieo. Xác suất của biến cố “ số
a
b
c
¯
chia hết cho 45” là
A
.
1
216
B
.
1
54
C
.
1
72...
Đọc tiếp
Gieo ngẫu nhiên một con súc sắc 3 lần liên tiếp. Gọi a,b,c lần lượt là số chấm xuất hiện ở 3 lần gieo. Xác suất của biến cố “ số a b c ¯ chia hết cho 45” là
A . 1 216
B . 1 54
C . 1 72
D . 1 108
Chọn C
Không gian mẫu: “ gieo ngẫu nhiên một con súc sắc 3 lần liên tiếp”
![]()
Biến cố A: “ số a b c ¯ chia hết cho 45”
a b c ¯ chia hết cho 45 ⇔ a b c ¯ chia hết cho cả 5 và 9
Vì
a
b
c
¯
chia hết cho 5 nên ![]() là số chấm xuất hiện của súc sắc khi gieo).
là số chấm xuất hiện của súc sắc khi gieo).
Vì a b c ¯ chia hết cho 9 mà c = 5 => a + b + 5 chia hết cho 9.
Các cặp số (a;b) sao cho ![]() mà a+b+5 chia hết cho 9 là: (1;3), (3;1), (2;2)
mà a+b+5 chia hết cho 9 là: (1;3), (3;1), (2;2)
Do đó: n(A) = 3.

Đúng 0
Bình luận (0)
gieo 1 con súc sắc cân đối và đồng chất 1 lần. tính xác xác suất của biến cố ''Số chấm xuất hiện chia hết cho 2''
Gọi T là biến cố "Số chấm xuất hiện chia hết cho 2".
\(\Rightarrow\left|\Omega\right|=6\)
\(\left|\Omega_T\right|=3\)
\(\Rightarrow P\left(T\right)=\dfrac{\left|\Omega_T\right|}{\left|\Omega\right|}=\dfrac{1}{2}\)
Đúng 0
Bình luận (0)
Gieo ngẫu nhiên một con súc sắc cân đối và đồng chất 2 lần. Tính xác suất của các biến cố
A: “ Mặt 6 chấm xuất hiện ở lần gieo đầu tiên”
B: “Số chấm ở 2 lần gieo như nhau”
C: “Tổng số chấm xuất hiện ở hai lần gieo bằng 9”
Xem thêm câu trả lời
Gieo con súc sắc hai lần. Biến cố A là biến cố để sau hai lần gieo có ít nhất một mặt 6 chấm: A. A{(1,6),(2,6),(3,6),(4,6),(5,6),(6,6)(6,1),(6,2),(6,3),(6,4),(6,5)} B. A{(6,1),(6,2),(6,3),(6,4),(6,5)} C. A {(1,6),(2,6),(3,6),(4,6),(5,6)} D. A{(1,6),((2,6),(3,6),(4,6),(5,6),(6,6)}
Đọc tiếp
Gieo con súc sắc hai lần. Biến cố A là biến cố để sau hai lần gieo có ít nhất một mặt 6 chấm:
A. A={(1,6),(2,6),(3,6),(4,6),(5,6),(6,6)(6,1),(6,2),(6,3),(6,4),(6,5)}
B. A={(6,1),(6,2),(6,3),(6,4),(6,5)}
C. A= {(1,6),(2,6),(3,6),(4,6),(5,6)}
D. A={(1,6),((2,6),(3,6),(4,6),(5,6),(6,6)}
Gieo con súc sắc hai lần. Biến cố A là biến cố để sau hai lần gieo có ít nhất một mặt 6 chấm:
Đọc tiếp
Gieo con súc sắc hai lần. Biến cố A là biến cố để sau hai lần gieo có ít nhất một mặt 6 chấm:

![]()
![]()
![]()
Một con súc sắc được gieo ba lần. Quan sát số chấm xuất hiện:
a) Xây dựng không gian mẫu.
b) Xác định các biến cố sau:
A. "Tổng số chấm trong ba lần gieo là 6";
B. "Số chấm trong lần gieo thứ nhất bằng tổng các số chấm của lần gieo thứ hai và thứ ba".
a) Ω = {(i, j, k) |1 ≤ i, j, k ≤ 6} gồm các chỉnh hợp chập 3 của 6 (số chấm).

Đúng 0
Bình luận (0)
Gieo một con xúc sắc 4 lần. Tìm xác suất của biến cố B: “ Mặt 3 chấm xuất hiện đúng một lần” A.
P
(
A
)
5
324
B.
P
(
A
)
5
32
C.
P
(
A
)
3
−
5
6
4
D.
P...
Đọc tiếp
Gieo một con xúc sắc 4 lần. Tìm xác suất của biến cố B: “ Mặt 3 chấm xuất hiện đúng một lần”
A. P ( A ) = 5 324
B. P ( A ) = 5 32
C. P ( A ) = 3 − 5 6 4
D. P ( A ) = 2 − 5 6 4
Gọi B i là biến cố “ mặt 3 chấm xuất hiện lần thứ i” với i =1;2; 3; 4
Khi đó: B i ¯ là biến cố “ Mặt 3 chấm không xuất hiện lần thứ i”
Ta có: A = B 1 ¯ . B 2 . B 3 . B 4 ∪ B 1 . B 2 ¯ . B 3 . B 4 ∪ B 1 . B 2 . B 3 ¯ . B 4 ∪ B 1 . B 2 . B 3 . B 4 ¯
Suy ra :
P A = P B 1 P B 2 P B 3 P B 4 + P B 1 P B 2 P B 3 P B 4 + P B 1 P B 2 P B 3 P B 4 + P B 1 P B 2 P B 3 P B 4
Mà : P ( B i ) = 1 6 ⇒ P ( B i ¯ ) = 1 − 1 6 = 5 6 .
Do đó: P ( A ) = 4. 1 6 3 . 5 6 = 5 324 .
Chọn đáp án A
Đúng 0
Bình luận (0)