Tìm nghiệm nguyên dương nhỏ nhất của pt: x²-15y²=1

Những câu hỏi liên quan
tìm nghiệm nguyên dương nhỏ nhất của hệ pt
a, x=5y+3 và x=11x+7
b, x+2y+3z=20 và 3x+5y+4z=37
Tìm nghiệm nguyên của PT: 6x+15y+10z=3
tìm nghiệm nguyên của pt
6x+15y+10z=3
Tìm nghiệm nguyên dương nhỏ nhất của bpt
f
(
x
)
|
x
+
1
|
+
|
x
-
4
|
-
7
0
A. x 4 B. x 5 C. x 6 D. x 7
Đọc tiếp
Tìm nghiệm nguyên dương nhỏ nhất của bpt
f ( x ) = | x + 1 | + | x - 4 | - 7 > 0
A. x = 4
B. x = 5
C. x= 6
D. x = 7
Chọn C
Ta có
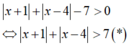
Bảng xét dấu
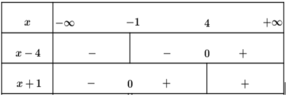
+ Trường hợp x ≤ - 1,(8) trở thành: -x-1-x+ 4 > 7 hay x < -4
So với trường hợp đang xét ta có tập nghiệm S1 = (- ∞,-4)
+ Trường hợp -1 < x ≤4,
( *) trở thành: x+1-x+4> 7
hay 5> 7 (vô lý)
Do đó, tập nghiệm ![]()
+ Trường hợp x > 4
(*) trở thành: x+ 1+ x-4> 7 hay x> 5
So với trường hợp đang xét ta có tập nghiệm S3 = (5, +∞)
Vậy ![]()
Do đó; x= 6 thỏa YCBT
Đúng 0
Bình luận (0)
22. Tìm nghiệm dương nhỏ nhất của PT: \(3\sin^2x+2\sin x\cos x-\cos^2x=0\)
23. Giải PT: \(\sqrt{3}\cos x+2\sin^2\left(\dfrac{x}{2}-\dfrac{\pi}{1}\right)=1\)
\(\sqrt{3}cosx+2sin^2\left(\dfrac{x}{2}-\pi\right)=1\)
\(\Leftrightarrow\sqrt{3}cosx+2sin^2\dfrac{x}{2}=1\)
\(\Leftrightarrow\sqrt{3}cosx-cosx=0\Leftrightarrow cosx=0\Leftrightarrow x=\dfrac{\pi}{2}+k\pi\) ( k thuộc Z )
Vậy ...
Đúng 0
Bình luận (0)
22.
Nhận thấy \(cosx=0\) không phải nghiệm, chia 2 vế cho \(cos^2x\)
\(3tan^2x+2tanx-1=0\)
\(\Leftrightarrow\left[{}\begin{matrix}tanx=-1\\tanx=\dfrac{1}{3}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{4}+k\pi\\x=arctan\left(\dfrac{1}{3}\right)+k\pi\end{matrix}\right.\)
Nghiệm dương nhỏ nhất của pt là: \(x=arctan\left(\dfrac{1}{3}\right)\)
Đúng 0
Bình luận (0)
22. PT đã cho tương đương
3 - 4cos2x + 2 sinxcosx = 0
⇔ 3 - 2 - 2cos2x + sin2x = 0
⇔ 1 - 2cos2x + sin2x = 0
⇔ 1 + sin2x = 2cos2x
⇔ sin\(\dfrac{\pi}{2}\) + sin2x = 2cos2x
⇔ \(2sin\left(\dfrac{\pi}{4}+x\right).cos\left(\dfrac{\pi}{4}-x\right)\) = 2cos2x
Do \(\left(\dfrac{\pi}{4}-x\right)+\left(\dfrac{\pi}{4}+x\right)=\dfrac{\pi}{2}\)
⇒ \(sin\left(\dfrac{\pi}{4}+x\right)=cos\left(\dfrac{\pi}{4}-x\right)\)
Vậy sin2\(\left(x+\dfrac{\pi}{4}\right)\) = cos2x
Cái này là hiển nhiên ????
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
1. tìm nghiệm nguyên dương của pt: 5(x+y+z+t) +10 = 2xyzt. bài này lm mãi k ra :)) :P
2. tìm nghiệm nguyên dương của pt: y^4 +y^2 = x^4 + x^3 + x^2 +x
xin câu tl chi tiết ak...
Mấy bạnn giải chii tiết raa giúp mik với nhaa Câu 1: nghiệm dương nhỏ nhất của pt tan x=tan (6π/5) A. x=π/5 B. x=6π/5 C. x=6/5 D. x=6π Câu 2: tìm nghiệm thuộc đoạn [0;π] của pt cot 2x=cot(π/2-x) A. 2 B. 3 C.1 D.4 Câu 3: tìm tổng các nghiệm thuộc khoảng (-π/2;π/2) của pt 4sin²2x-1=0 A.0 B. π/6 C. π/3 D. π Câu 4: tìm tổng các nghiệm của pt cos(x+π/4)=1/2 trong khoảng (-π;π) A. π/2 B. -π/2 C. -3π/2 D. π/4
1) Tìm giá trị nhỏ nhất của biểu thức A = 2 2 2 2013 x x với x là số nguyên.
2) Tìm nghiệm nguyên dương của phương trình x y z xyz .
a) Cho 3 số x,y,z thỏa mãn: x+y+z0 tìm giá trị lớn nhất cuarBxy+yz+zxb)đa thức f(x) x2+px+q với pin Z,qin ZCmr tồn tại số nguyên k để f(k) f(2008).f(2009)c)tìm 3 số nguyên dương x,y thỏa mãn 3xy+x+15y - 440d)Cho số tự nhiên a(29)2009 , b là tổng các chữ số của b, d là tổng các chữ số của c. tính de)Cho pt ẩn x frac{2x-m}{x-2}+frac{x-1}{x+2}3Tìm m để pt có nghiệm dương
Đọc tiếp
a) Cho 3 số x,y,z thỏa mãn: x+y+z=0 tìm giá trị lớn nhất cuarB=xy+yz+zx
b)đa thức f(x) = x2+px+q với \(p\in Z,q\in Z\)Cmr tồn tại số nguyên k để f(k)= f(2008).f(2009)
c)tìm 3 số nguyên dương x,y thỏa mãn 3xy+x+15y - 44=0
d)Cho số tự nhiên a=(29)2009 , b là tổng các chữ số của b, d là tổng các chữ số của c. tính d
e)Cho pt ẩn x \(\frac{2x-m}{x-2}+\frac{x-1}{x+2}=3\)Tìm m để pt có nghiệm dương
1. cho các số thực dương x,y,z t/mãn: x2 + y2 + z2 = 1
Cmr: \(\frac{x}{y^2+z^2}\) + \(\frac{y}{x^2+z^2}+\frac{z}{x^2+y^2}\ge\) \(\frac{3\sqrt{3}}{2}\)
2. Cho x,y thỏa mãn \(\hept{\begin{cases}xy\ge0\\x^2+y^2=1\end{cases}}\)
Tìm GTNN,GTLN của \(S=x\sqrt{1+y}+y\sqrt{1+x}\)
3. Cho \(\hept{\begin{cases}xy\ne0\\xy\left(x+y\right)=x^2+y^2-xy\end{cases}}\)
Tìm GTLN của \(A=\frac{1}{x^3}+\frac{1}{y^3}\)
4. Cho tam giác ABC; đường thẳng đi qua trọng tâm G và tâm đường tròn nội tiếp I vuông góc với đường phân giác trong của góc C. Gọi a,b,c là độ dài 3 canh tương ứng với 3 đỉnh A,B,C.
Cmr: \(\frac{1}{a}+\frac{1}{b}\le\frac{2}{c}\)
Đúng 0
Bình luận (0)
ui má. đúng mấy bài tập thầy tui cho ôn. giờ đang loay hoay
Đúng 0
Bình luận (0)



















