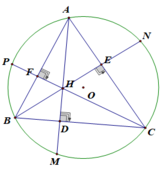
Cho tam giác ABC nhọn, có AD, BE và CF là các đường cao cắt nhau tại H. Biết N đối xứng H qua E, P đối xứng H qua F và M đối xứng H qua D. CMR: \(\frac{AM}{AD}+\frac{BN}{BE}+\frac{CP}{CF}=4\)

Những câu hỏi liên quan
Cho tam giác ABC nhọn có 3 đường cao AD,BE,CF đồng quy tại H. M,N,P lần lượt là các điểm đối xứng của H qua BC,AC và AB.Tính AM/AD+BN/BE+CP/CF
Cho tam giác ABC có 3 đường cao AD, BE, CF cắt nhau tại H.Gọi M, N, S theo thứ tự là điểm đối xứng của H qua BC, CA, AB.
CMR \(\frac{AM}{AD}+\frac{BN}{BE}+\frac{CS}{CF}=4\)
Lời giải:
\(\frac{AM}{AD}+\frac{BN}{BE}+\frac{CS}{CF}=4\Leftrightarrow \frac{DM}{AD}+\frac{EN}{BE}+\frac{FS}{CF}=1\)
\(\Leftrightarrow \frac{HD}{AD}+\frac{EH}{BE}+\frac{HF}{CF}=1\) \((\star)\)
Gọi diện tích của các tam giác \(AFH, BFH, BHD, DHC, EHC, AEH\) lần lượt là \(a,b,c,d,e,f\)
Ta có :
\(\left\{\begin{matrix} \frac{DH}{AD}=\frac{S_{BHD}}{S_{BAD}}=\frac{S_{CHD}}{S_{ADC}}\\ \frac{EH}{BE}=\frac{S_{AEH}}{S_{ABE}}=\frac{S_{CHE}}{S_{EBC}}\\ \frac{HF}{CF}=\frac{S_{BFH}}{S_{BFC}}=\frac{S_{FAH}}{S_{FAC}}\end{matrix}\right.\)\(\Leftrightarrow \left\{\begin{matrix} \frac{DH}{AD}=\frac{c}{a+b+c}=\frac{d}{e+f+d}=\frac{c+d}{a+b+c+d+e+f}\\ \frac{EH}{BE}=\frac{f}{a+b+f}=\frac{e}{e+c+d}=\frac{e+f}{a+b+c+d+e+f}\\ \frac{HF}{CF}=\frac{b}{b+c+d}=\frac{a}{a+f+e}=\frac{a+b}{a+b+c+d+e+f}\end{matrix}\right.\)
\(\Rightarrow \frac{DH}{AD}+\frac{EH}{BE}+\frac{HF}{CF}=1\)
Ta có \((\star)\) nên phép cm hoàn tất.
Đúng 0
Bình luận (0)
Cho tam giác ABC có 3 đường cao AD, BE, CF cắt nhau tại H.Gọi M, N, S theo thứ tự là điểm đối xứng của H qua BC, CA, AB.
CMR \(\frac{AM}{AD}+\frac{BN}{BE}+\frac{CS}{CF}\)=4
Cho tam giác ABC nhọn có ba dường cao AD, BE, CF đồng quy tại H. M,N,P lần lượt là các điểm đối xứng của H qua BC, AC và AB. Tính AM / AD + BN / BE + CP / CF
Cho tam giác nhọn ABC có ba đường cao AD, BE, CF đồng quy tai H. M, N, P lần lượt là các điểm đối xứng của H qua BC, AC và AB . TÍnh AM/AD + BN/BE + CP/CF
1, Cho tam giác ABC nhọn có AB,AC, các đường cao AD;BE;CF cắt nhau tại H.
b, Gọi M là điểm đối xứng của H qua D. Giao điểm của EF với AM là N. CMR: HN.AD=AN.DM
cho tam giác nhọn ABC,đường cao AD. Gọi M là điểm đối xứng với d qua AB, N là điểm đối xứng với d qua AB, N là điểm đối xứng với với D qua AC. MN cắt AC và và AB tương tự tại E và F CMR: AD,BE,CF đồng quy
Cho tam giác ABC có ba góc nhọn nội tiếp (O) ,các đường cao AD ,BE,CF cắt nhau tại H và cắt đường tròn lần lượt tại M,N,P
cm H và M đối xứng nhau qua AB
Sửa đề: M đối xứng H qua BC
Gọi AD là đường kính, I là giao của HD và BC
góc ABD=1/2*sđ cung AD=90 độ
=>BD//CH
góc ACD=1/2*sđ cung AD=90 độ
=>CD//BH
mà BD//CH
nên BHCD là hình bình hành
=>BC căt HD tại trung điểm của mỗi đường
=>I là trung điểm chung của HD và BC và BH//CD
góc AMD=1/2*sđ cung AD=90 độ
=>MD vuông góc AM
=>MD//BC
=>BCDM là hình thang cân
=>góc MBC=góc DCB=góc HBC
=>BC là phân giác của góc HBM
mà BC là trung tuyến của ΔHBM
nên ΔHMB cân tại B
=>BC là trug trực của MH
=>M đối xứng H qua BC
Đúng 1
Bình luận (0)
Cho tam giác ABC có 3 góc nhọn nội tiếp đường tròn (O). Các đường cao AD, BE, CF cắt nhau tại H và cắt đường tròn (O) lần lượt tại M, N, P. Chứng minh rằng:
d) H và M đối xứng nhau qua BC
d) Tam giác ADB vuông tại D có: ∠(A1) + ∠(ABC) = 90o (1)
Tam giác BCF vuông tại F có: ∠(C1) + ∠(ABC) = 90o (2)
Từ (1)và (2) ⇒ ∠(A1) = ∠(C1)
Mặt khác, ta có: ∠( A 1 ) = ∠( C 2 ) ( 2 góc nội tiếp cùng chắn cung BM)
⇒ ∠( C 1 ) = ∠( C 2 )
⇒ CD là tia phân giác của góc HCM
Xét tam giác HCM có: CD vừa là tia phân giác vừa là đường cao (CD⊥HD)
⇒ Δ HCM cân tại C
⇒ CD cũng là trung tuyến của của HM hay H và M đối xứng với nhau qua D.
Đúng 0
Bình luận (0)













