a/ Kéo dài SM cắt CD ở N

\(\left(SBM\right)\equiv\left(SBN\right)\)

\(\left(SBN\right)\cap\left(ABCD\right)=BN\)

\(BN\cap CD=\left\{N\right\}\Rightarrow CD\cap\left(SBM\right)=\left\{N\right\}\)

b/ Tương tự như câu a, ta sẽ tiếp tục sử dụng (SNB) bởi (SNB)=(SMB)

\(AC\cap BN=\left\{H\right\}\Rightarrow H=\left(SAC\right)\cap\left(SBN\right)\)

\(\Rightarrow\left(SAC\right)\cap\left(SBN\right)=SH\Rightarrow\left(SAC\right)\cap\left(SBM\right)=SH\)

c/ \(SH\cap BM=\left\{I\right\}\Rightarrow I=BM\cap\left(SAC\right)\)

d/ \(SC\subset\left(SCD\right)\)

\(AB\cap CD=\left\{K\right\}\Rightarrow\left(ABM\right)\cap\left(SCD\right)=MK\) (câu d luôn :v)

\(\Rightarrow MK\cap SC=\left\{P\right\}\Rightarrow P=\left(ABM\right)\cap SC\)

Nối BC và AD kéo dài cắt nhau tại F

\(\Rightarrow SF=\left(SBC\right)\cap\left(SAD\right)\)

Trong mp (SCD), nối CM kéo dài cắt SD tại G

\(\Rightarrow AG=\left(AMC\right)\cap\left(SAD\right)\)

Trong mp (SCD), nối SM kéo dài cắt CD tại E

\(\Rightarrow AE=\left(SAM\right)\cap\left(ABCD\right)\)

Trong mp (ABCD), nối BE cắt AC tại H

\(\Rightarrow SH=\left(SBM\right)\cap\left(SAC\right)\)

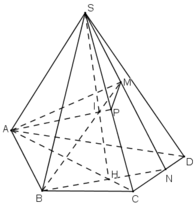
a) SM, CD cùng thuộc (SCD) và không song song.

Gọi N là giao điểm của SM và CD.

⇒ N ∈ CD và N ∈ SM

Mà SM ⊂ (SMB)

⇒ N ∈ (SMB)

⇒ N = (SMB) ∩ CD.

b) N ∈ CD ⊂ (ABCD)

⇒ BN ⊂ (ABCD)

⇒ AC; BN cùng nằm trong (ABCD) và không song song

Gọi giao điểm của AC và BN là H.

+ H ∈ AC ⊂ (SAC)

+ H ∈ BN ⊂ (SBM)

⇒ H ∈ (SAC) ∩ (SBM)

Dễ dàng nhận thấy giao điểm thứ hai của (SAC) và (SBM) là S

⇒ (SAC) ∩ (SBM) = SH.

c) Trong mp(SBM), gọi giao điểm của BM và SH là I, ta có:

I ∈ BM

I ∈ SH ⊂ (SAC).

⇒ I = BM ∩ (SAC).

) Trong mp(SAC), gọi giao điểm của AI và SC là P.

+ P ∈ AI, mà AI ⊂ (AMB) ⇒ P ∈ (AMB)

⇒ P = (AMB) ∩ SC.

Lại có P ∈ SC, mà SC ⊂ (SCD) ⇒ P ∈ (SCD).

⇒ P ∈ (AMB) ∩ (SCD).

Lại có: M ∈ (SCD) (gt)

⇒ M ∈ (MAB) ∩ (SCD)

Vậy giao điểm của (MAB) và (SCD) là đường thẳng MP.

a) Trong (SCD) kéo dài SM cắt CD tại N, Chứng minh N thuộc (SBM)

b) (SBM) ≡ (SBN). Giao tuyến cần tìm là SO

c) Trong (SBN) ta có MB giao SO tại I

d) Trong (ABCD) , ta có AB giao CD tại K, Trong (SCD), ta có KQ giao SC tại P

Từ đó suy ra được giao tuyến của hai mặt phẳng (SCD) và (ABM) là KQ.

Gọi I = DM  SC (cùng trong (SDC))

Chọn (BID) chứa BM 

I  (BID)  (SAC)

Gọi E= BD  AC (cùng trong (ABCD))

E thuộc BD con (BID)

E thuộc AC con (SAC)

=> E thuộc (BID)  (SAC)

(BID)  (SAC) = IE

Gọi H=IE  BM (cùng trong (BID))

H thuộc BM

H thuộc IE con (SAC)

=> H = BM  (SAC)