giải phương trình : x4-5x3+8x2-5x+1
mn giúp e vs . cần gấp lắm ạ :"(
Phương trình x 4 − 5 x 3 + 8 x 2 − 10 x + 4 = 0 có bao nhiêu nghiệm nguyên?
A. 4
B. 1
C. 2
D. 0
x 4 − 5 x 3 + 8 x 2 − 10 x + 4 = 0 ⇔ ( x 4 + 4 x 2 + 4 ) − 5 x 3 + 4 x 2 − 10 x = 0
⇔ x 2 + 2 2 − 5 x 3 + 10 x + 4 x 2 = 0 ⇔ x 2 + 2 2 − 5 x x 2 + 2 + 4 x 2 = 0
Đặt t = x 2 + 2 ta được t 2 − 5 t x + 4 x 2 = 0 ⇔ t − x t − 4 x = 0
Hay phương trình đã cho ⇔ x 2 − x + 2 x 2 − 4 x + 2 = 0
⇔ x 2 − x + 2 = 0 ( V N ) x 2 − 4 x + 2 = 0 ⇔ x = 2 ± 2
Vậy phương trình không có nghiệm nguyên
Đáp án cần chọn là: D
giúp vs ạ
1.xác định hệ số a,b,c của phương trình bâc hai 4x2+ 5x-2019=0
2. tính chu vi hình tròn có bán kính bằng 5cm
3.cho hàm số y=(5m+10)x2 tìm m để hàm số đồng biến khi x>0
4.Vẽ đồ thị hàm số (P):y=X2
5 Giải phương trình trùng phương x4- 8x2-9 =0
6 tính tổng và tính tích các nghiệm của PT 2x3-3x-2=0
5:
=>x^4-9x^2+x^2-9=0
=>x^2-9=0
=>x=3; x=-3
4: 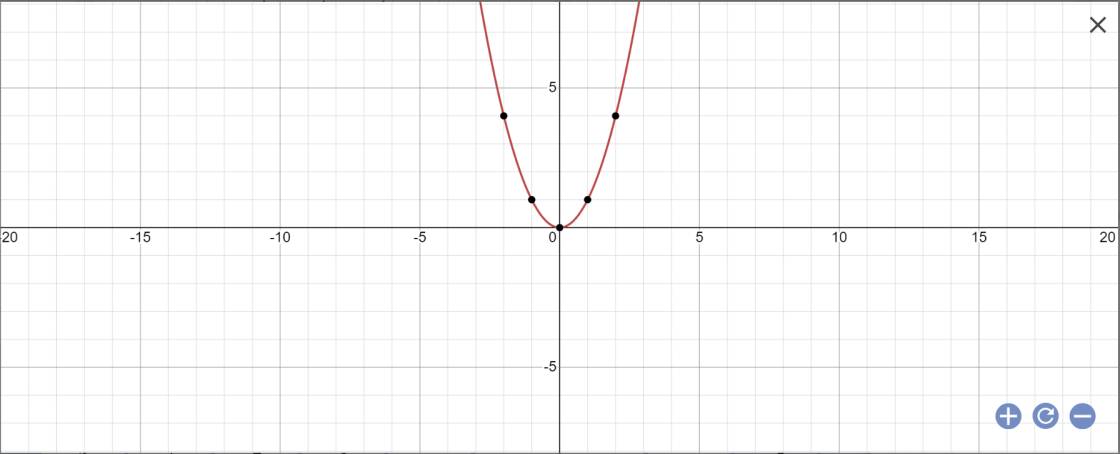
3: HS đồng biến khi x>0
=>5m+10>0
=>m>-2
Giải bất phương trình
x4-10x^3+35x^2+24>0
Mng giúp e vs ak e đag cần gấp e cảm ơn ak
\(x^4-10x^3+35x^2+24>0\)
\(\Leftrightarrow x^4-2.5.x^3+\left(5x\right)^2+10x^2+24>0\)
\(\Leftrightarrow\left(x^2-5x\right)^2+10x^2+24>0\)
\(\Leftrightarrow x^2\left(x-5\right)^2+10x^2+24>0\)(luôn đúng)
Vậy nghiệm của bất phương trình \(x\in R\)
Ta có 27^5=3^3^5=3^15
243^3=3^5^3=3^15
Vậy A=B
2^300=2^(3.100)=2^3^100=8^100
3^200=3^(2.100)=3^2^100=9^100
Vậy A<B
Giúp mik vs mik cần gấp ạ Đề toán 8 - Ôn tập
Câu 1: Giải các phương trình sau:
a. 7x + 21 = 0
b. 3x – 2 = 2x – 3
c. 5x – 2x – 24 = 0
Câu 2: Giải các phương trình sau:
a. (2x + 1)(x – 1) = 0
b. (2x – 3)(-x + 7) = 0
c. (x + 3)3 – 9(x + 3) = 0
Câu 3: Giải các phương trình sau:

Câu 1:
a) Ta có: 7x+21=0
\(\Leftrightarrow7x=-21\)
hay x=-3
Vậy: S={-3}
b) Ta có: 3x-2=2x-3
\(\Leftrightarrow3x-2-2x+3=0\)
\(\Leftrightarrow x+1=0\)
hay x=-1
Vậy: S={-1}
c) Ta có: 5x-2x-24=0
\(\Leftrightarrow3x=24\)
hay x=8
Vậy: S={8}
Câu 2:
a) Ta có: \(\left(2x+1\right)\left(x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+1=0\\x-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=-1\\x=1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{2}\\x=1\end{matrix}\right.\)
Vậy: \(S=\left\{-\dfrac{1}{2};1\right\}\)
b) Ta có: \(\left(2x-3\right)\left(-x+7\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-3=0\\-x+7=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=3\\-x=-7\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=7\end{matrix}\right.\)
Vậy: \(S=\left\{\dfrac{3}{2};7\right\}\)
c) Ta có: \(\left(x+3\right)^3-9\left(x+3\right)=0\)
\(\Leftrightarrow\left(x+3\right)\left[\left(x+3\right)^2-9\right]=0\)
\(\Leftrightarrow\left(x+3\right)\left(x+3-3\right)\left(x+3+3\right)=0\)
\(\Leftrightarrow x\left(x+3\right)\left(x+6\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x+3=0\\x+6=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-3\\x=-6\end{matrix}\right.\)
Vậy: S={0;-3;-6}
Trong mặt phẳng Õy cho đường tròn (C) qua phép quay tâm O(0;0) góc quay -pi/2 là đường tròn phương trình GIÚP EM VS Ạ E CẦN GẤP LẮM

tìm điều kiện xác định và giải phương trình giúp mik vs gấp lắm ạ
b: ĐKXD: x<>1/5; x<>3
PT\(\Leftrightarrow\dfrac{3}{5x-1}-\dfrac{2}{x-3}=\dfrac{-4}{\left(5x-1\right)\left(x-3\right)}\)
=>3x-9-10x+2=-4
=>-7x-7=-4
=>-7x=3
=>x=-3/7
a: ĐKXĐ: x<>2/3; x<>-2/3
\(PT\Leftrightarrow\left(3x+2\right)^2-6\left(3x-2\right)=9x\)
=>9x^2+12x+4-18x+12-9x=0
=>9x^2-15x+16=0
=>\(x\in\varnothing\)
c: ĐKXĐ: x<>1/4; x<>-1/4
PT =>-3(4x+1)=2(4x-1)-6x-8
=>-12x-3=8x-2-6x-8
=>-12x-3=2x-10
=>-14x=-7
=>x=1/2
d: ĐKXĐ: x<>0; x<>2
\(\Leftrightarrow\dfrac{5-x}{4x\left(x-2\right)}+\dfrac{7}{8x}=\dfrac{x-1}{2x\left(x-2\right)}+\dfrac{1}{8\left(x-2\right)}\)
=>2(5-x)+7(x-2)=4(x-1)+x
=>10-2x+7x-14=4x-4+x
=>5x-4=5x-4
=>0x=0(luôn đung)
Vậy: S=R\{0;2}
e: DKXĐ: x<>0
PT \(\Leftrightarrow\dfrac{\left(x+1\right)\left(x^2-x+1\right)-\left(x-1\right)\left(x^2+x+1\right)}{\left(x^2+x+1\right)\left(x^2-x+1\right)}=\dfrac{3}{x\left(x^2+x+1\right)\left(x^2-x+1\right)}\)
=>x(x^3+1-x^3+1)=3
=>2x=3
=>x=3/2
tìm điều kiện xác định và giải phương trình giúp mik vs gấp lắm ạ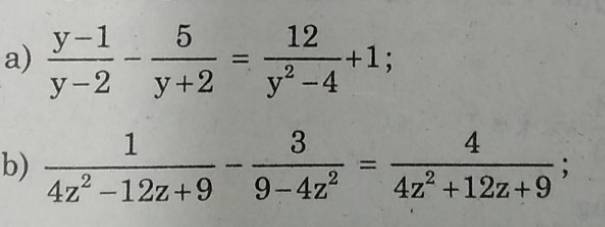
\(a,\dfrac{y-1}{y-2}-\dfrac{5}{y+2}=\dfrac{12}{y^2-4}+1\left(ĐKXĐ:x\ne\pm2\right)\)
\(\Leftrightarrow\dfrac{\left(y-1\right)\left(y+2\right)}{\left(y-2\right)\left(y+2\right)}-\dfrac{5\left(y-2\right)}{\left(y-2\right)\left(y+2\right)}-\dfrac{12}{\left(y-2\right)\left(y+2\right)}-\dfrac{\left(y-2\right)\left(y+2\right)}{\left(y-2\right)\left(y+2\right)}=0\)
\(\Leftrightarrow\dfrac{y^2+y-2}{\left(y-2\right)\left(y+2\right)}-\dfrac{5y-10}{\left(y-2\right)\left(y+2\right)}-\dfrac{12}{\left(y-2\right)\left(y+2\right)}-\dfrac{y^2-4}{\left(y-2\right)\left(y+2\right)}=0\)
\(\Leftrightarrow\dfrac{y^2+y-2-5y+10-12-y^2+4}{\left(y-2\right)\left(y+2\right)}=0\)
\(\Rightarrow-4y=0\)
\(\Leftrightarrow y=0\left(tm\right)\)
\(b,\dfrac{1}{4z^2-12z+9}-\dfrac{3}{9-4z^2}=\dfrac{4}{4z^2+12z+9}\left(ĐKXĐ:z\ne\pm\dfrac{3}{2}\right)\)
\(\Leftrightarrow\dfrac{1}{\left(2z-3\right)^2}+\dfrac{3}{\left(2z-3\right)\left(2z+3\right)}-\dfrac{4}{\left(2z+3\right)^2}=0\)
\(⇔\dfrac{\left(2z+3\right)^2}{\left(2z-3\right)^2\left(2z+3\right)^2}+\dfrac{3\left(2z-3\right)\left(2z+3\right)}{\left(2z-3\right)^2\left(2z+3\right)^2}-\dfrac{4\left(2z-3\right)^2}{\left(2z-3\right)^2\left(2z+3\right)^2}=0\)
\(\Leftrightarrow\dfrac{4z^2+12z+9}{\left(2z-3\right)^2\left(2z+3\right)^2}+\dfrac{12z^2-27}{\left(2z-3\right)^2\left(2z+3\right)^2}-\dfrac{16z^2-48z+36}{\left(2z-3\right)^2\left(2z+3\right)^2}=0\)
\(\Leftrightarrow\dfrac{4z^2+12z+9+12z^2-27-16z^2+48z-36}{\left(2z-3\right)^2\left(2z+3\right)^2}=0\)
\(\Rightarrow60z-54=0\)
\(\Leftrightarrow60z=54\)
\(\Leftrightarrow z=\dfrac{9}{10}\left(tm\right).\)
\(a,\dfrac{y-1}{y-2}-\dfrac{5}{y+2}=\dfrac{12}{y^2-4}+1\left(dkxd:y\ne\pm2\right)\)
\(\Leftrightarrow\dfrac{\left(y-1\right)\left(y+2\right)-5\left(y-2\right)-12-y^2+4}{y^2-4}=0\)
\(\Leftrightarrow y^2+2y-y-2-5y+10-12-y^2+4=0\)
\(\Leftrightarrow-4y=0\)
\(\Leftrightarrow y=0\left(tmdk\right)\)
Vậy \(S=\left\{0\right\}\)
\(b,\dfrac{1}{4z^2-12z+9}-\dfrac{3}{9-4z^2}=\dfrac{4}{4z^2+12z+9}\)
\(\Leftrightarrow\dfrac{1}{\left(2z-3\right)^2}-\dfrac{3}{\left(2z-3\right)\left(2z+3\right)}=\dfrac{4}{\left(2z+3\right)^2}\left(dkxd:z\ne\pm\dfrac{3}{2}\right)\)
\(\Leftrightarrow\left(2z+3\right)^2-3\left(4z^2-9\right)-4\left(2z-3\right)^2=0\)
\(\Leftrightarrow4z^2+12z+9-12z^2+27-4\left(4z^2-12z+9\right)=0\)
\(\Leftrightarrow4z^2+12z+9-12z^2+27-16z^2+48z-36=0\)
\(\Leftrightarrow-24z^2+60z=0\)
\(\Leftrightarrow-12z\left(2z-5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}-12z=0\\2z-5=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}z=0\left(tmdk\right)\\z=\dfrac{5}{2}\left(tmdk\right)\end{matrix}\right.\)
Vậy \(S=\left\{0;\dfrac{5}{2}\right\}\)
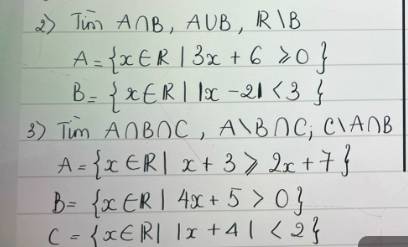
giúp e vs ạ, e cần gấp lắm ạ
`2)`
`@` Xét `3x+6 >= 0<=>x >= -2`
`=>A=[-2;+oo)`
`@` Xét `|x-2| < 3`
`<=>-3 < x-2 < 3`
`<=>-1 < x < 5=>B=(-1;5)`
Có: `A nn B=(-1;5)`
`A uu B=[-2;+oo)`
`R \\ B=(-oo;-1]uu[5;+oo)`
_______
`3)`
`@` Xét `x+3 >= 2x+7<=>x <= -4=>A=(-oo;-4]`
`@` Xét `4x+5 > 0<=>x > -5/4=>B=(-5/4;+oo)`
`@` Xét `|x+4| < 2<=>-2 < x+4 < 2<=>-6 < x < -2 =>C=(-6;-2)`
Có: `A nn B nn C=\emptyset`
`A \\ B nn C=(-6;-4]`
`C \\ A nn B=\emptyset`.

giúp e vs ạ, e cần gấp lắm ạ
Bài 4:
Theo định lý sin ta có:
\(\dfrac{AC}{sinB}=\dfrac{BC}{sinA}\)
\(\Rightarrow BC=a=\dfrac{b\cdot sinA}{sinB}=\dfrac{2\cdot sin60^o}{sin45^o}=\sqrt{6}\)
\(\Rightarrow\widehat{C}=180^o-60^o-45^o=75^o\)
\(\dfrac{AC}{sinB}=\dfrac{AB}{sinC}\)
\(\Rightarrow AB=c=\dfrac{b\cdot sinC}{sinB}=\dfrac{2\cdot sin75^o}{sin45^o}=1+\sqrt{3}\)
Diện tích tam giác ABC là:
\(S_{ABC}=\dfrac{1}{2}\cdot AC\cdot AB\cdot sinA=\dfrac{1}{2}\cdot2\cdot\left(1+\sqrt{3}\right)\cdot sin75^o=\dfrac{\sqrt{6}+2\sqrt{2}}{2}\) (đvdt)
Bán kình hình tròn tam giác ABC khi đó là:
\(S_{ABC}=\dfrac{abc}{4R}\)
\(\Rightarrow R=\dfrac{abc}{4S_{ABC}}=\dfrac{2\cdot\left(1+\sqrt{3}\right)\cdot\sqrt{6}}{4\cdot\left(\dfrac{\sqrt{6}+2\sqrt{2}}{2}\right)}=3-\sqrt{3}\)
Bài 3:
a) Xét tam giác ABC theo định lý côsin ta có:
\(cosC=\dfrac{a^2+b^2-c^2}{2ab}=\dfrac{8^2+10^2-13^2}{2\cdot8\cdot10}=-0,03125\)
\(\Rightarrow\widehat{C}=cos^{-1}-0,03125\approx91^o>90^o\)
Nên tam giác ABC có góc C là góc tù
c) Theo hệ thức Heron ta có diện tích tam giác ABC là:
\(S_{ABC}=\sqrt{p\cdot\left(p-a\right)\cdot\left(p-b\right)\cdot\left(p-c\right)}\)
\(\Rightarrow S_{ABC}=\sqrt{\dfrac{8+10+13}{2}\cdot\left(\dfrac{8+10+13}{2}-8\right)\cdot\left(\dfrac{8+10+13}{2}-10\right)\cdot\left(\dfrac{8+10+13}{2}-13\right)}\)
\(\Rightarrow S_{ABC}\approx40\) (đvdt)
b) Bán kính đường tròn ngoại tiếp tam giác ABC là:
\(S_{ABC}=\dfrac{abc}{4R}\)
\(\Rightarrow R=\dfrac{abc}{4S_{ABC}}=\dfrac{8\cdot10\cdot13}{4\cdot40}=6,5\)