x2 phần a2y2=1 phần a2y2 + b2x2 và x2+y2=1 . CM x2010 phần a1005 + y2010 phần b1005 =2 phần (a+b)1005

Những câu hỏi liên quan
Phân tích đa thức thành nhân tử bằng hằng đẳng thức
a) a2y2+b2x2- 2abxy
b) 100 - (3x-y)2
\(a,a^2y^2+b^2x^2-2abxy\\ =\left(ay\right)^2-2abxy+\left(bx\right)^2\\ =\left(ay-bx\right)^2=\left(bx-ay\right)^2\\ ---\\ b,100-\left(3x-y\right)^2\\ =10^2-\left(3x-y\right)^2\\ =\left(10-3x+y\right)\left(10+3x-y\right)\)
Đúng 3
Bình luận (0)
a) \(=\left(ay\right)^2-2abxy+\left(bx\right)^2\)
\(=\left(ay-bx\right)^2\)
b) \(100-\left(3x-y\right)^2\)
\(=10^2-\left(3x-y\right)^2\)
\(=\left(10-3x+y\right)\left(10+3x-y\right)\)
Đúng 2
Bình luận (0)
Thực hiện phép tính
a) (-x3+2x4-4-x2+7x):(x2+x-1)
b) y phần 2x2-xy + 4x phần y2-2xy
c) 6x+48 phần 7x-7 : x2-64 phần x2-2x+1
a: \(\dfrac{2x^4-x^3-x^2+7x-4}{x^2+x-1}\)
\(=\dfrac{2x^4+2x^3-2x^2-3x^3-3x^2+3x+4x^2+4x-4}{x^2+x-1}\)
=2x^2-3x+4
b: \(=\dfrac{y}{x\left(2x-y\right)}+\dfrac{4x}{y\left(y-2x\right)}\)
\(=\dfrac{y^2-4x^2}{xy\left(2x-y\right)}=\dfrac{-\left(2x-y\right)\left(2x+y\right)}{xy\left(2x-y\right)}=\dfrac{-2x-y}{xy}\)
c: \(=\dfrac{6\left(x+8\right)}{7\left(x-1\right)}\cdot\dfrac{\left(x-1\right)^2}{\left(x-8\right)\left(x+8\right)}=\dfrac{6\left(x-1\right)}{7\left(x-8\right)}\)
Đúng 0
Bình luận (0)
cho x và y là 2 đại lượng tỉ lệ thuận. Tính x1 và y1 biết y1-x1=-1 phần 4 và x2=4 phần 5 và y2=8 phần 15
Giải phươn trình sau
a) x2-4=(x-2)(3x+1)
b) x-1 phần 4 + x+1 phần 3 = x-1 phần 2
c) x phần x+3 - x+2 phần x-3 - -16 phần x2-9 = 0
a: =>(x-2)(3x+1)-(x-2)(x+2)=0
=>(x-2)(3x+1-x-2)=0
=>(x-2)(2x-1)=0
=>x=1/2 hoặc x=2
b: =>3(x-1)+4(x+1)=6(x-1)
=>3x-3+4x+4=6x-6
=>7x+1=6x-6
=>x=-7
c: =>x(x-3)-(x+2)(x+3)+16=0
=>x^2-3x-x^2-5x-6+16=0
=>10-8x=0
=>x=5/4
Đúng 0
Bình luận (0)
Giải phương trình
a) 1 phần x-1 - 3x2 phần x3+1 = 2x phần x2+x+1
b) x phần 3 + x = x phần 6 + 2x+1 phần 2
a:
Sửa đề: \(\dfrac{1}{x-1}-\dfrac{3x^2}{x^3-1}=\dfrac{2x}{x^2+x+1}\)
=>x^2+x+1-3x^2=2x(x-1)
=>-2x^2+x+1-2x^2+2x=0
=>-4x^2+3x+1=0
=>4x^2-3x-1=0
=>4x^2-4x+x-1=0
=>(x-1)(4x+1)=0
=>x=1(loại) hoặc x=-1/4(nhận)
b: =>2x+6x=x+3(2x+1)
=>x+6x+3=8x
=>7x+3=8x
=>-x=-3
=>x=3(nhận)
Đúng 0
Bình luận (0)
Parabol (P):
y
x
2
chia đường tròn (C):
x
2
+
y
2
2
thành hai phần (tham khảo hình vẽ bên) có tỷ số diện tích (phần nhỏ chia phần lớn) bằng A.
3
π
+
2
12
π
B.
3...
Đọc tiếp
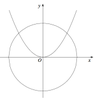
Parabol (P): y = x 2 chia đường tròn (C): x 2 + y 2 = 2 thành hai phần (tham khảo hình vẽ bên) có tỷ số diện tích (phần nhỏ chia phần lớn) bằng
A. 3 π + 2 12 π
B. 3 π + 2 9 π - 2
C. 9 π - 2 12 π
D. 9 π - 2 18 π + 12
Cho tỉ lệ thức:x/y=3/5
Tính giá trí các biểu thức:
A=3x + y (phần) 4x-y
B=x2-3x+y2( phần) x2+3xy-y2
Tìm x
1 phần 1.3 + 1 phần 3.5+ 1 phần 5.7+..+1 phần x+(X+2)=1005 phần 2011
Cho parabol
(
P
)
:
y
2
2
x
và đường tròn
(
C
)
:
x
2
+
y
2
8
.
(P) chia (C) thành hai phần. Tìm tỉ số diện tích của hai phần đó. A.
9
π
+
2
3...
Đọc tiếp
Cho parabol ( P ) : y 2 = 2 x và đường tròn ( C ) : x 2 + y 2 = 8 . (P) chia (C) thành hai phần. Tìm tỉ số diện tích của hai phần đó.
A. 9 π + 2 3 π - 2
B. 9 π - 2 3 π - 2
C. 9 π + 2 3 π + 2
D. 9 π - 2 3 π + 2
















