\(sorry\)

bạn vòa đường link này là dc https://olm.vn/hoi-dap/detail/11276671901.html

Ta có : x, y là hai số nguyên tố ( chẵn và lẻ )

Vì y² do tổng của hai số bất kì ( x² + 45 ) nên y² phải là số nguyên tố lẻ ( nếu y² là số nguyên tố chẵn, tức là 2 thì vô lí ! )

Vậy x² là số nguyên tố chẵn ( chỉ có một số nguyên tố chẵn, là 2 )

Ta được :

2² + 45 = y²

⇒⇒y² = 49

giúp mình vs

Bài a

Bài b:

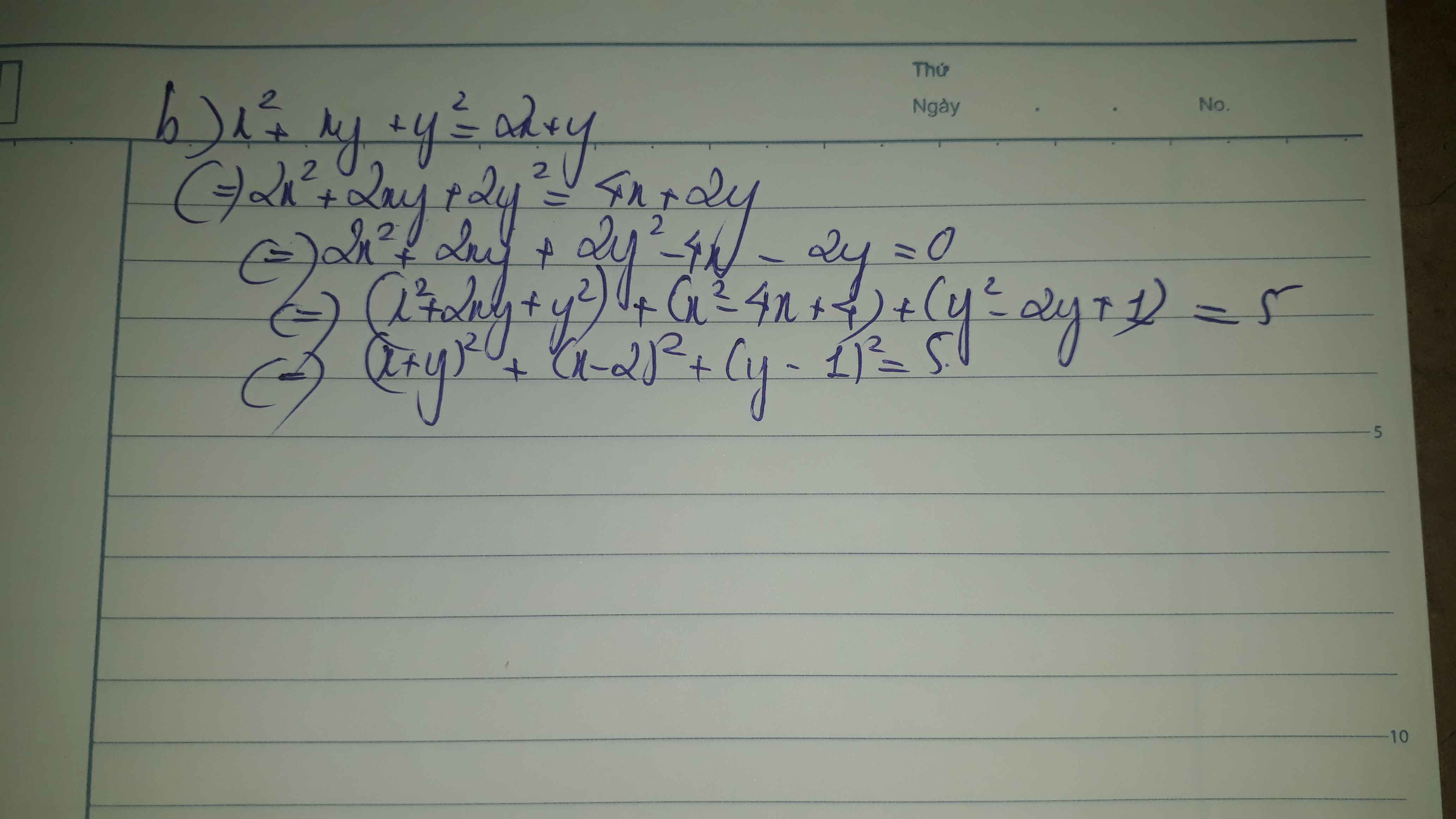
Đến đoạn này bạn xét như bài a nhé.

Bài c cũng tương tự câu b, bạn nhân 2 vào cả 2 vế, chuyển vế đổi dấu và ghép vế trái lại thành tổng các bình phương, vế phải là một số tự nhiên. Đến đoạn này cũng xét như bài a.

Còn bài d và bài e thì mình chưa biết làm thế nào, nhưng mình nghĩ vế trái sẽ là bình phương của tổng hoặc hiệu của x và y, vế phải là bình phương của tổng hoặc hiệu của y và một số nào đó. Tuy nhiên chắc là sẽ phải nhân thêm một số nào đó bởi vì nếu không nhân khi làm sẽ ra phân số, không xét được.

a) \(6xy+4x-9y-7=0\)

  \(\Leftrightarrow2x.\left(3y+2\right)-9y-6-1=0\)

\(\Leftrightarrow2x.\left(3y+x\right)-3.\left(3y+2\right)=1\)

\(\Leftrightarrow\left(2x-3\right).\left(3y+2\right)=1\)

Mà \(x,y\in Z\Rightarrow2x-3;3y+2\in Z\)

Tự làm típ

\(A=x^3+y^3+xy\)

\(A=\left(x+y\right)\left(x^2-xy+y^2\right)+xy\)

\(A=x^2-xy+y^2+xy\)( vì \(x+y=1\))

\(A=x^2+y^2\)

Áp dụng bất đẳng thức Bunhiakovxky ta có :

\(\left(1^2+1^2\right)\left(x^2+y^2\right)\ge\left(x\cdot1+y\cdot1\right)^2=\left(x+y\right)^2=1\)

\(\Leftrightarrow2\left(x^2+y^2\right)\ge1\)

\(\Leftrightarrow x^2+y^2\ge\frac{1}{2}\)

Hay \(x^3+y^3+xy\ge\frac{1}{2}\)

Dấu "=" xảy ra \(\Leftrightarrow x=y=\frac{1}{2}\)

LOADING...

bài 2 nhân p vs x+y+xy rồi t định áp dụng bđt (x+y+z)(1/x+1/y+1/z)>=9 nhưng vướng