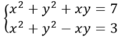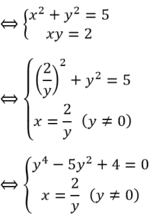Tìm nghiệm nguyên:x2+y2=3-xy
Những câu hỏi liên quan
1 tháng 9 2021 lúc 16:55
Giải phương trình nghiệm nguyên:
x2-y2=1998
https://hoc24.vn/cau-hoi/chung-minh-rang-phuong-trinh-sau-khong-co-nghiem-nguyena-x2-y21998b-x2y21994.262907021445
Đúng 1
Bình luận (3)
y2 = x2 - 1998
x2 = 1998 + y2
y = \(\sqrt{x^2-1998}\)
x = \(\sqrt{1998+y^2}\)
y = x - \(\sqrt{1998}\)
x = y + \(\sqrt{1998}\)
Đúng 1
Bình luận (1)
3 tháng 8 2021 lúc 15:20
giải phương trình nghiệm nguyên:
x2-x=y2-1
Số nghiệm của hệ phương trình
x
2
+
y
2
+
x
y
7...
Đọc tiếp
Số nghiệm của hệ phương trình x 2 + y 2 + x y = 7 x 2 + y 2 - x y = 3 là:
A. 2
B. 1
C. 3
D. 4
2x2+xy-y2-5=0 tìm nghiệm dương
Giải pt nghiệm nguyên:
1) 3(x2-xy+y2)=7(x+y)
2) 5(x2+xy+y2)=7(x+2y)
Tìm nghiệm nguyên của phương trình : x2 - xy +y2 = x-y
<=>x^2+y^2-x-y-xy=0
<=>2x^2+2y^2-2x-2y-2xy=0
<=>(x-y)^2+(x-1)^2+(y-1)^2=2
mà 2=0+1+1=1+0+1=1+1+0
(phần này tách số 2 ra thành tổng 3 số chính phương)
Xét trường hợp 1:
(x-y)^2=0
(x-1)^2=1
(y-1)^2=1
Giải ra ta được x=2, y=2
Tương tự xét các trường hợp còn lại.
Kết quả: 5 nghiệm: (2;2) ; (1;0) ; (1;2) ; (0;1) ; (2;1)
Đúng 0
Bình luận (0)
x2 - xy + y2 = x - y
<=> x2 - xy + y2 - x + y = 0
<=> x ( x - y) + y2 - ( x - y) = 0
<=> (x-1)(x-y)y2 =0
Đúng 0
Bình luận (0)
Cho hệ phương trình:
2
x
2
+
x
y
−
y
2
0
x
2
−...
Đọc tiếp
Cho hệ phương trình: 2 x 2 + x y − y 2 = 0 x 2 − x y − y 2 + 3 x + 7 y + 3 = 0 . Các cặp nghiệm (x; y) sao cho x, y đều là các số nguyên là:
A. (2; −2), (3; −3).
B. (−2; 2), (−3; 3).
C. (1; −1), (3; −3).
D. (−1; 1), (−4; 4).
Phương trình 1 ⇔ x + y 2 x - y = 0 ⇔ x = − y 2 x = y
Trường hợp 1: x = - y thay vào (2) ta được x 2 - 4 x + 3 = 0 ⇔ x = 1 x = 3
Suy ra hệ phương trình có hai nghiệm là (1; −1), (3; −3).
Trường hợp 2: 2 x = y thay vào (2) ta được - 5 x 2 + 17 x + 3 = 0 phương trình này không có nghiệm nguyên.
Vậy các cặp nghiệm (x; y) sao cho x, y đều là các số nguyên là (1; −1) và (3; −3).
Đáp án cần chọn là: C
Đúng 0
Bình luận (0)
Biết cặp số (x; y) là nghiệm của hệ
x
+
y
2
m
x
2
+
y
2
2
m...
Đọc tiếp
Biết cặp số (x; y) là nghiệm của hệ x + y = 2 m x 2 + y 2 = 2 m + 2 . Tìm giá trị của m để P = xy – 3 (x + y) đạt giá trị nhỏ nhất.
A. m = - 7 2
B. m = −7
C. m = 7
D. m = 7 2
Tìm các giá trị
a
,
b
∈
ℝ
để hệ phương trình
x
y
-
1
x
y...
Đọc tiếp
Tìm các giá trị a , b ∈ ℝ để hệ phương trình x y - 1 x y + 1 = a x 2 + y 2 = b (x>0) có nghiệm duy nhất.
A. a=0;b=1
B. a=1,b=2
C. a=0; 0 < b ≤ 1
D. a=0;b=2
Tìm nghiệm nguyên của phương trình sau:
(x2 - x +1)(y2 + xy) = 3x - 1
bài này dễ quá 😖 mấy a/c giúp e với