
a, Rút gọn b,Tìm GTLN
cho A= /x-7/-/x+5/
a, rút gọn A
b, tìm GTLN của A
Cho : B = 0,(21) - x - ( x -0,(4) )
a. Rút gọn B
b. Tìm GTLN của B
cho P \(=\frac{20-x-\sqrt{x}}{\sqrt{x}+5}\)
a) rút gọn P
b) Tìm x để P đạt GTLN. tính GTLN đó
Ta có P=\(\frac{20-x-5\sqrt{x}+4\sqrt{x}}{\sqrt{x}+5}\)
P=\(\frac{\sqrt{x}\left(4-\sqrt{x}\right)+5\left(4-\sqrt{x}\right)}{\sqrt{x}+5}\)
P=\(\frac{\left(\sqrt{x}+5\right).\left(4-\sqrt{x}\right)}{\sqrt{x}+5}\)
P=\(4-\sqrt{x}\)
b) Ta có P=\(4-\sqrt{x}\)\(\le\)4 với mọi x\(\ge0\)
=> P đạt GTLN là 4 khi \(\sqrt{x}=0\)
=> x=0
Rút gọn và tìm GTLN: A = 4(x+2) - (2x+1)(2x-1)
\(A=4\left(x+2\right)-\left(2x+1\right)\left(2x-1\right)\)
\(A=4x+8-4x^2+1\)
\(A=-\left(4x^2-4x+4\right)+13\)
\(A=-\left(2x+2\right)^2+13\)
Vì \(-\left(2x+2\right)^2\le0\forall x\)
\(\Rightarrow-\left(2x+2\right)^2+13\le13\forall x\)
\(\Rightarrow A_{max}=13\)khi và chỉ khi \(-\left(2x+2\right)^2=0\Rightarrow x=-1\)
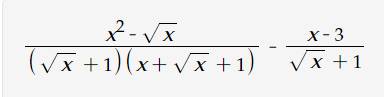
rút gọn và tìm gtln của nó
ĐKXĐ: x>=0
\(A=\dfrac{\sqrt{x}\left(x\sqrt{x}-1\right)}{\left(\sqrt{x}+1\right)\left(x+\sqrt{x}+1\right)}-\dfrac{x-3}{\sqrt{x}+1}\)
\(=\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{\sqrt{x}+1}-\dfrac{x-3}{\sqrt{x}+1}\)
\(=\dfrac{x-\sqrt{x}-x+3}{\sqrt{x}+1}=\dfrac{-\sqrt{x}+3}{\sqrt{x}+1}\)
\(=\dfrac{-\sqrt{x}-1+4}{\sqrt{x}+1}=-1+\dfrac{4}{\sqrt{x}+1}\)
\(\dfrac{4}{\sqrt{x}+1}< =\dfrac{4}{1}=4\)
=>\(\dfrac{4}{\sqrt{x}+1}-1< =4-1=3\)
Dấu = xảy ra khi x=0
1 cho biểu thức A=5x(xy^2-2xy)-5x^2y^2. Rút gọn A .b) Tính GT của A khi x=-1/2 ,y=2
2. Tìm GTLN của bt A = |x-7|-|x-9|.Q= |x-2|+|x-8| b) tìm GTLN của bt P= 9-2|x-3|
Cho P= (1/(√x+2))-(5/(x-√x-6))-((√x-2)/(3-√x))
a, Rút gọn P
b, tìm GTLN của P
\(M=\frac{3x^2+3}{x^4+2x^3+7x^2+2x+6}\)
a)Rút gọn M
b)Tìm GTLN của M
a, \(M=\frac{3\left(x^2+1\right)}{\left(x^4+x^2\right)+\left(2x^3+2x\right)+\left(6x^2+6x\right)}=\frac{3\left(x^2+1\right)}{x^2\left(x^2+1\right)+2x\left(x^2+1\right)+6\left(x^2+1\right)}=\frac{3\left(x^2+1\right)}{\left(x^2+2x+6\right)\left(x^2+1\right)}=\frac{3}{x^2+2x+6}\)
b, ta có: \(M=\frac{3}{x^2+2x+6}=\frac{3}{\left(x^2+2x+1\right)+5}=\frac{3}{\left(x+1\right)^2+5}\)
Vì \(\left(x+1\right)^2\ge0\Rightarrow\left(x+1\right)^2+5\ge5\Rightarrow\frac{1}{\left(x+1\right)^2+5}\le\frac{1}{5}\Rightarrow M=\frac{3}{\left(x+1\right)^2+5}\le\frac{3}{5}\)
Dấu "=" xảy ra <=>x+1=0 <=> x=-1
rút gọn A=((1/x- căn x) +(1/căn x -1)) / ((căn x+1)/(căn x -1)^2)
tìm GTLN của P=A-16 căn x
`A=(1/(x-sqrtx)+1/(sqrtx-1)):(sqrtx+1)/(sqrtx-1)^2`
`=((sqrtx+1)/(x-sqrtx)).(sqrtx-1)^2/(sqrtx+1)`
`=(sqrtx-1)^2/(x-sqrtx)`
`=(sqrtx-1)/sqrtx`