a)gọi M = giao điểm của CE và DF 
xét tg EBC và tg FCD có: 
AB= BC <> AB/2 = BC/2 <> EB = FC ( E,F lần lượt là trung điểm của AB,BC ) 
^EBC = ^FCD = 90* ( ABCD là hình vuông) 
BC= DC ( ABCD là hình vuông ) 
=> tg EBC = tg FCD 
=> ^ECB = ^FDC 
mà ^FDC + ^DFC = 90* ( do tg DFC vuông tại C) 
<> ^ECB + ^DFC = 90* 
=> tg KMC vuông tại M 
hay DF vuông góc EC 

b) Kẻ AH // EC ( H la trung diem CD ) 
EC vuong DF tai M ( tu cau a ) 
=> AH vuong DF tai K 
* xet 2 tg vuong CMD va HKD co 
^CMD = ^HKD = 90¤ 
^DHK = ^DCM ( 2 goc dong vi) 
=> tgCMD ~ tg HKD 
HD/CD = KD/MD = 1/2 
=> KD = KM 
* xet 2 tg vuong AKD va AKM co 
AK chung 
goc AKD = goc AKM = 90¤ 
KM = KD 
=> tg AKM = tg AKD 
=> AD = AM

a) Gọi M = giao điểm của CE và DF

xét tg EBC và tg FCD có:

AB= BC <> AB/2 = BC/2 <> EB = FC ( E,F lần lượt là trung điểm của AB,BC )

^EBC = ^FCD = 90* ( ABCD là hình vuông)

BC= DC ( ABCD là hình vuông )

=> tg EBC = tg FCD

=> ^ECB = ^FDC

mà ^FDC + ^DFC = 90* ( do tg DFC vuông tại C)

<> ^ECB + ^DFC = 90*

=> tg KMC vuông tại M

hay DF vuông góc EC

b) Kẻ AH // EC ( H la trung diem CD )

EC vuông DF tại M ( tu cau a )

=> AH vuông DF tai K

xét 2 tg vuông CMD và HKD có

^CMD = ^HKD = 90¤

^DHK = ^DCM ( 2 góc đồng vị )

=> tgCMD ~ tg HKD

HD/CD = KD/MD = 1/2

=> KD = KM

xét 2 tg vuông AKD và AKM có

AK chung

góc AKD = góc AKM = 90¤

KM = KD

=> tg AKM = tg AKD

=> AD = AM

Học tốt 🐱

a: Xét ΔCDF vuông tại C và ΔBCE vuông tại B có

CD=BC

CF=BE

Do đó: ΔCDF=ΔBCE
=>góc CDF=góc BCE

=>góc BCE+góc MFC=góc DFC+góc CDF=90 độ

=>CE vuông góc với DF

b: Gọi Klà trung điểm của CD và N là giao của AK và DF

Xét tứ giác AECK có

AE//CK

AE=CK

Do dó: AECK là hình bình hành

SUy ra: AK=CE và AK//CE

=>AK vuông góc với DF

Xét ΔDMC có

K là trung điểm của DC

KN//MC

Do đó: N là trung điểm của DM

Xét ΔAMD có

AN vừa là đường cao, vừa là đường trung tuyến

nên ΔAMD cân tại A

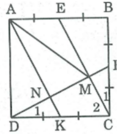
Xét  ∆ BEC và ∆ CFD , ta có: BE = CF (gt)

∠ B =  ∠ C = 90 0

BC = CD (gt)

Suy ra:  ∆ BEC =  ∆ CFD (c.g.c) ⇒ ∠C1 = ∠D1

Lại có:  ∠ C 1  +  ∠ C 2  =  90 0

Suy ra:  ∠ D 1  +  ∠ C 2  =  90 0

Trong ΔDCM có  ∠ D 1  +  ∠ C 2  =  90 0

Suy ra:  ∠ (DMC) =  90 0

Vậy CE ⊥ DF

a: Xét ΔCDF vuông tại C và ΔBCE vuông tại B có

CD=BC

CF=BE

Do đó: ΔCDF=ΔBCE
=>góc CDF=góc BCE

=>góc BCE+góc MFC=góc DFC+góc CDF=90 độ

=>CE vuông góc với DF

b: Gọi Klà trung điểm của CD và N là giao của AK và DF

Xét tứ giác AECK có

AE//CK

AE=CK

Do dó: AECK là hình bình hành

SUy ra: AK=CE và AK//CE

=>AK vuông góc với DF

Xét ΔDMC có

K là trung điểm của DC

KN//MC

Do đó: N là trung điểm của DM

Xét ΔAMD có

AN vừa là đường cao, vừa là đường trung tuyến

nên ΔAMD cân tại A

Bài 3: 

a: Xét ΔCDF vuông tại C và ΔBCE vuông tại B có

CD=BC

CF=BE

Do đó: ΔCDF=ΔBCE
=>góc CDF=góc BCE

=>góc BCE+góc MFC=góc DFC+góc CDF=90 độ

=>CE vuông góc với DF

b: Gọi Klà trung điểm của CD và N là giao của AK và DF

Xét tứ giác AECK có

AE//CK

AE=CK

Do dó: AECK là hình bình hành

SUy ra: AK=CE và AK//CE

=>AK vuông góc với DF

Xét ΔDMC có

K là trung điểm của DC

KN//MC

Do đó: N là trung điểm của DM

Xét ΔAMD có

AN vừa là đường cao, vừa là đường trung tuyến

nên ΔAMD cân tại A

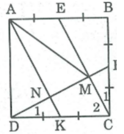
Gọi K là trung điểm của DC, AK cắt DF tại N.

* Xét tứ giác AKCE, ta có: AB // CD hay AE // CK

AE = 1/2 AB (gt)

CK = 1/2 CD (theo cách vẽ)

AB = CD ( Vì ABCD là hình vuông)

Suy ra: AE = CK nên tứ giác AKCE là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau) ⇒ AK// CE

DF ⊥ CE (chứng minh trên) ⇒ AK ⊥ DF hay AN ⊥ DM

* Trong ∆ DMC, ta có: DK = KC và KN // CM

Nên DN = MN (tính chất đường trung bình của tam giác)

Tam giác ADM có AN là đường cao đồng thời là đường trung tuyến

Suy ra:  ∆ ADM cân tại A

Vậy AD = AM.