Xét ∆ BEC và ∆ CFD , ta có: BE = CF (gt)
∠ B = ∠ C = 90 0
BC = CD (gt)
Suy ra: ∆ BEC = ∆ CFD (c.g.c) ⇒ ∠C1 = ∠D1
Lại có: ∠ C 1 + ∠ C 2 = 90 0
Suy ra: ∠ D 1 + ∠ C 2 = 90 0
Trong ΔDCM có ∠ D 1 + ∠ C 2 = 90 0
Suy ra: ∠ (DMC) = 90 0
Vậy CE ⊥ DF

Xét ∆ BEC và ∆ CFD , ta có: BE = CF (gt)
∠ B = ∠ C = 90 0
BC = CD (gt)
Suy ra: ∆ BEC = ∆ CFD (c.g.c) ⇒ ∠C1 = ∠D1
Lại có: ∠ C 1 + ∠ C 2 = 90 0
Suy ra: ∠ D 1 + ∠ C 2 = 90 0
Trong ΔDCM có ∠ D 1 + ∠ C 2 = 90 0
Suy ra: ∠ (DMC) = 90 0
Vậy CE ⊥ DF
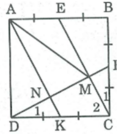
Cho hình vuông ABCD, gọi E, F thứ tự là trung điểm của AB, BC.
a) CMR: CE vuông góc với DF.
b) Gọi M là giao điểm của CE và DF. Chứng minh rằng: AM=AD
Cho hình vuông ABCD. Gọi E, F theo thứ tự là trung điểm của AB, BC. Gọi M là giao điểm của CE và DF. Chứng minh rằng AM = AB
Cho hình vuông ABCD. Gọi E, F theo thứ tự là trung điểm của AB, BC. Gọi M là giao điểm của CE và DF. Chứng minh rằng AM = AD.
cho hình vuông abcd , gọi e,f thứ tự là trung điểm của ab và bc . cmr ce vuông góc với df
Cho hình vuông ABCD . Gọi E, F theo thứ tự là trung điểm của AB, BC.
a) CMR : CF vuông góc với DF.
b) Gọi M là giao điểm của CE và DF . CMR : AM = AD
Cho hình vuông ABCD. Gọi E, F, K lần lượt là trung điểm của AB, BC, CD. 1) Chứng minh: AECK là hình bình hành 2) Chứng minh: DF vuông góc với CE tại M. 3) AK cắt DF tại N. Chứng minh N là trung điểm của DM
4) Chứng minh: AM = AB
Cho hình vuông ABCD. E, F theo thứ tự là trung điểm AB, BC.
a. CMR: CE vuông góc với DF.
b. M là giao điểm CE, DF. CMR: MA = MB.
Cho hình vuông ABCD. Gọi E,F lần lượt là trung điểm của AB,BC. I là giao điểm của CE và DF
chứng minh :
1 CE=DF, CE vuông góc với DF
2 kẻ AH vuông góc với DE, AH cắt CD tại G. Chứng minh:a, GC=AE=GD
b, AB=AI
Bài 3: Hình vuông ABCD. E thuộc AB: EA=EB, F thuộc CB: FC=FB. CMR:
a) CE vuông góc với DF
b) CE cắt DF tại M. CMR: AM=AD
Bài 4: Hình vuông ABCD, AB=BC=CD=DA=4cm. I là trung điểm của AD, E đối xứng với A qua BI, BE cắt CD ở F. Tính DF=?
Bài 5: Hình vuông ABCD. E, F, I theo thứ tự là trung điểm của BC, CD, DA. H, K theo thứ tự là giao điểm của IB, DE với AF. CMR:
a) AH=HK
b) IB vuông góc với AF
c) BA=BK