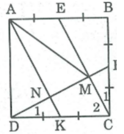
Gọi K là trung điểm của DC, AK cắt DF tại N.
* Xét tứ giác AKCE, ta có: AB // CD hay AE // CK
AE = 1/2 AB (gt)
CK = 1/2 CD (theo cách vẽ)
AB = CD ( Vì ABCD là hình vuông)
Suy ra: AE = CK nên tứ giác AKCE là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau) ⇒ AK// CE
DF ⊥ CE (chứng minh trên) ⇒ AK ⊥ DF hay AN ⊥ DM
* Trong ∆ DMC, ta có: DK = KC và KN // CM
Nên DN = MN (tính chất đường trung bình của tam giác)
Tam giác ADM có AN là đường cao đồng thời là đường trung tuyến
Suy ra: ∆ ADM cân tại A
Vậy AD = AM.









