Bài 4: Cho hình bình hành ABCD có AB 2AD. Gọi E, F thứ tự là trung điểm của AB và CD. a. Các tứ giác AEFD, AECF là hình gì? Vì sao? b. gọi M là giao điểm của AF và DE, gọi N là giao điểm của BF và CE. Chứng minh rằng tứ giác EMFN là hình chữ nhật. c. Hình bình hành ABCD cần thêm điều kiện gì thì EMFN là hình vuông?Bài 5: Cho tam giác ABC vuông tại A, D là trung điểm của BC. Gọi M, N lần lượt là hình chiếu của điểm D trên cạnh AB, AC. a. Chứng minh tứ giác ANDM là hình chữ nhật. b. Gọi I, K...
Đọc tiếp
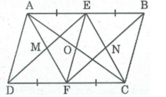
Bài 4: Cho hình bình hành ABCD có AB = 2AD. Gọi E, F thứ tự là trung điểm của AB và CD.
a. Các tứ giác AEFD, AECF là hình gì? Vì sao?
b. gọi M là giao điểm của AF và DE, gọi N là giao điểm của BF và CE. Chứng minh rằng tứ giác EMFN là hình chữ nhật.
c. Hình bình hành ABCD cần thêm điều kiện gì thì EMFN là hình vuông?
Bài 5: Cho tam giác ABC vuông tại A, D là trung điểm của BC. Gọi M, N lần lượt là hình chiếu của điểm D trên cạnh AB, AC.
a. Chứng minh tứ giác ANDM là hình chữ nhật.
b. Gọi I, K lần lượt là điểm đối xứng của N, M qua D. Tứ giác MNKI là hình gì? Vì sao?
c. Kẻ đường cao AH của tam giác ABC (H thuộc BC). Tính số đo góc MHN.
Bài 6. Cho tam giác ABC vuông tại A, đường trung tuyến AM. Gọi D là trung điểm của AB, E là điểm đối xứng với M qua D.
a. Chứng minh rằng điểm E đối xứng với điểm M qua AB.
b. Các tứ giác AEMC, AEBM là hình gì? Vì sao?
c. Cho BC = 4cm, tính chu vi tứ giác AEBM.