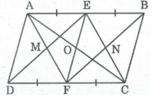
Gọi O là giao điểm của AC và EF
Tứ giác AECF là hình bình hành ⇒ OE = OF
Tứ giác EMFN là hình bình hành nên hai đường chéo cắt nhau tại trung điểm của mỗi đường.
Suy ra: MN đi qua trung điểm O của EF.
Vậy AC, EF, MN đồng quy tại O.
cho hình bình hành ABCD gọi E,F theo thứ tự là trung điểm của AB,CD Gọi M là giao điểm của AF và DE, N là giao điểm BF và CE
a) CMR EMFN là hình bình hành
b) Các Đường thẳng AC, EF, MN Đồng quy
Cho hình bình hành ABCD. Gọi E, F là trung điểm AB,CD. Gọi M là giao điểm của AF và DE, N là giao điểm BF và CE. Chứng minh:
a) EMFN là hình bình hành
b) Các đường thẳng AC, EF, MN đồng quy
Cho hình bình hành ABCD. Gọi E, F là trung điểm AB,CD. Gọi M là giao điểm của AF và DE, N là giao điểm BF và CE. Chứng minh:
a) EMFN là hình bình hành
b) Các đường thẳng AC, EF, MN đồng quy
Cho Hình bình hành ABCD . Gọi E,F theo thứ tự là trung điển của AB,CD
Gọi M là giao điểm của F và DE ,N là giao điển của BF và CE
a) C/m : EMFN là hình bình hành
b)c/m các đường thẳng AC , EF , MN đồng quy
Hình bình hành:
1. Cho tứ giác ABC, gọi E, F là trung điểm của AB và CD; M, N, P, Q lần lượt là trung điểm các đoạn AF, CE, BF và DE. C Chứng minh rằng MNPQ là hình bình hành.
2. Cho hình bình hành ABCD. Các điểm E, F thuộc đường chéo AC sao cho AE = EF = FC. Gọi M là giao điểm của BF và CD; N là giao điểm của DE và AB. Chứng minh rằng:
a. M, N theo thứ tự là trung điểm của CD, AB.
b. EMFN là hình bình hành.
Cho hình hình hành ABCD. Gọi E, F theo thứ tự là trung điểm của AB, CD. Gọi M là giao điểm của AF và DE, N là giao điểm của BF và CE. Chứng minh rằng: EMNF là hình bình hành
cho hình bình hành ABCD gọi EF thứ tự tại trung điểm Của AB và CD, M là giao điểm của AF, DE, N là giao điểm của BF và CE. CMR:
a) DE=BF
b)tứ giác EMFN là hình bình hành
c) các đường thẳng AC, FE, MN đồng quy
d) gọi I, K lần lượt là giao điểm của AF và CE với BD. CMR: BK = KI = ID
Cho tứ giác ABCD. Gọi E, F theo thứ tự là trung điểm của AB và CD; M, N, P, Q lầ lượt là trung điểm của các đoạn thẳng AF, CE, BF và DE. Gọi I là giao điểm của MP và EF. Chứng minh rằng:
a) I là trung điểm của MP
b) MNPQ là hình bình hành
Cho hình bình hành ABCD. Gọi E, F thứ tự là trung điểm của AB và CD. M là giao điểm của AF và DE, N là giao điểm của BF và CE.
a) CMR: Tứ giác EMFN là hình bình hành
b) CMR: AC, EF, MN đồng quy
c) Gọi I, K lần lượt là giao điểm của AF và CE với BD. CMR: BK=KI=ID
