
Những câu hỏi liên quan
Cho hình bình hành ABCD có AB = 2AD. Gọi E là trung điểm AD, F là trung điểm CD. Gọi M là giao điểm của AF và DE, N là giao điểm của BF và CE. AECF là hình bình hành, AEDF là hình bình hành. Chứng minh rằng MN = EF
Ai giúp e vs ạ 8h30 e phải nộp rùi please
Xét tứ giác AECF có
AE//CF
AE=CF
Do đó: AECF là hình bình hành
Đúng 0
Bình luận (0)
hình bình hành abcd có điểm e f lần lượt là trung điểm AB,AC. M là giao điểm của DE,AF. N là giao điểm của BF,CE. Chưng minh EMFN là hình bình hành
Cho hình bình hành ABCD, ab=2ad. gọi E,F theo thứ tự là trung điểm của AB và CD
a) c/m tứ giác AECF là hình bình hành
b) c/m AF vuông góc DE
c) Gọi M là giao điểm của AF và DE, N là giao điểm của BF và CE.c/m EF=MN
d) Tính tỷ số diện tích của tam giác BEF và diện tích hình bình hành ABCD
Xem chi tiết
Cho hình bình hành ABCD có E, F theo thứ tự là trung điểm của AB, CD. Gọi giao điểm của AC với DE và BF theo thứ tự là M và N. Chứng minh rằng tứ giác EMFN là hình bình hành.
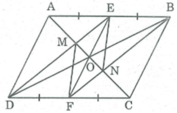
Xét ∆ EOM và ∆ FON có: ∠ (MEO) = ∠ (NFO) (so le trong do DE//BF)
OE = OF (tính chất hình bình hành)
∠ (MOE)= ∠ (NOF) (đối đỉnh )
Suy ra: ∆ EOM = ∆ FON (g.c.g) ⇒ OM = ON
Vậy tứ giác EMFN là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường).
Đúng 1
Bình luận (0)
Cho hình bình hành ABCD có E, F thuộc AC sao cho AE=EF=FC. Gọi M là giao điểm của BF và CD.N là giao điểm của DE và AB. CM
a) M, N lần lượt là trung điểm của CD và AB
b) Tứ giác EMFN là hình bình hành
Cho hình hình hành ABCD. Gọi E, F theo thứ tự là trung điểm của AB, CD. Gọi M là giao điểm của AF và DE, N là giao điểm của BF và CE. Chứng minh rằng: EMNF là hình bình hành
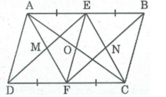
+) Ta có:
AE = 1/2 AB; CF = 1/2. CD ( vì E và F lần lượt là trung điểm của AB, CD).
Và AB = CD (tính chất hình bình hành)
Suy ra: AE = CF
+) Lại có: AB // CD ( vì ABCD là hình bình hành) nên AE //CF
Tứ giác AECF có hai cạnh đối AE, CF song song và bằng nhau nên là hình bình hành
⇒ AF //CE hay EN // FM (1)
Xét tứ giác BFDE ta có:
AB // CD (gt) hay BE // DF
BE = 1/2 AB (gt)
DF = 1/2 CD (gt)
AB = CD (tính chất hình bình hành)
Suy ra: BE = DF
Tứ giác BFDE là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau) ⇒ BF//DE hay EM // FN (2)
Từ (1) và (2) suy ra tứ giác EMFN là hình bình hành (theo định nghĩa hình bình hành)
Đúng 0
Bình luận (0)
Hình bình hành:1. Cho tứ giác ABC, gọi E, F là trung điểm của AB và CD; M, N, P, Q lần lượt là trung điểm các đoạn AF, CE, BF và DE. C Chứng minh rằng MNPQ là hình bình hành.2. Cho hình bình hành ABCD. Các điểm E, F thuộc đường chéo AC sao cho AE EF FC. Gọi M là giao điểm của BF và CD; N là giao điểm của DE và AB. Chứng minh rằng:a. M, N theo thứ tự là trung điểm của CD, AB.b. EMFN là hình bình hành.
Đọc tiếp
Hình bình hành:
1. Cho tứ giác ABC, gọi E, F là trung điểm của AB và CD; M, N, P, Q lần lượt là trung điểm các đoạn AF, CE, BF và DE. C Chứng minh rằng MNPQ là hình bình hành.
2. Cho hình bình hành ABCD. Các điểm E, F thuộc đường chéo AC sao cho AE = EF = FC. Gọi M là giao điểm của BF và CD; N là giao điểm của DE và AB. Chứng minh rằng:
a. M, N theo thứ tự là trung điểm của CD, AB.
b. EMFN là hình bình hành.
cho hình bình hành ABCD. E;F thuộc AC sao cho AE=EF=FC. gọi m là giao điểm của BF với CD. gọi N là giao điểm của DE và AB. chứng minh :
a/ M;N là trung điểm của CD;AB
b/ EMFN là hình bình hành
do ABCD là hình bình hành
=>AD//BC
=>\(\widehat{DAC}=\widehat{BCA}\)(so le)
Xét \(\Delta ADE\) và \(\Delta CBF\) có:
AD=BC( do ABCD là hình bình hành)
\(\widehat{DAC}=\widehat{BCA}\)(cmt)
AE=CF(gt)
=>\(\Delta ADE\)=\(\Delta CBF\)(c.g.c)
=>\(\widehat{AED}=\widehat{CFB}\)
Ta có:
\(\widehat{AED}=\widehat{NEC}(đối dỉnh) \)
\(\widehat{BFC}=\widehat{AFM}(đối đỉnh)\)
=>\(\widehat{NEC}=\widehat{AFM}\)
Mà hai góc này ở vị trí so le trong
=>DN//MB
=>EN//BF(1)
Lại có:
AE=EF(2)
=>AN=NB=> N là trung điểm của AB
MB//DN=>MF//DE(3)
Lại có: CF=EF(4)
Từ (3),(4)
=>CM=MD
=> M là trung điểm của CD
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD có E, F lần lượt là trung điểm của AB và CD. Gọi giao điểm của AC với DE và BF theo thứ tự là M và N
a) CM: các tứ giác DEBF, EMFN là hình bình hành
b) Hình bình hành ABCD cần thêm điều kiện gì để tứ giác MENF là hình thoi














