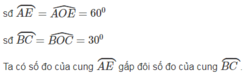Cho đường tròn $O$ đường kính $AB$ và dây cung $AC$. Chứng tỏ rằng $\text{sđ } \widehat{BAC}=\frac{1}{2} \text{sđ } \overgroup{BC}$.

Những câu hỏi liên quan
Cho đường tròn (O) đường kính AB và dây cung AC. Chứng minh rằng góc BAC = 1/2 sđ cung BC.
Cho đường tròn (O) đường kính AB và dây cung AC. Chứng minh rằng góc BAC = 1/2 sđ cung BC.
Giúp mình với!
Cho đường tròn (O) đường kính AB và dây cung AC. Chứng minh rằng góc BAC = 1/2 sđ cung BC.
Giúp mình với!
Ta có OA = OC = bán kính đường tròn (O)
=> Tam giác OAC cân tại O => \(\widehat{A_1}=\widehat{C_1}\)
Do \(\widehat{O_1}\) là góc ngoài tại O của tam giác OAC
=> \(\widehat{O_1}\) = \(\widehat{A_1}+\widehat{C_1}\) = 2.\(\widehat{A_1}\) hay \(\widehat{A_1}\) = \(\dfrac{1}{2}\).\(\widehat{O_1}\) (đpcm)
Đúng 1
Bình luận (0)
Cho đường tròn (O) đường kính AB và dây cung AC. Chứng minh rằng góc BAC = 1/2 sđ cung BC.
Giúp mình với!
Cho đường tròn (O) đường kính AB và dây cung AC. Chứng minh rằng góc BAC = 1/2 sđ cung BC.
Giúp mình với!
Trên đường tròn tâm O đường kính AB=2R , lấy điểm C sao cho sđ cung BC=60° . Hai tiếp tuyến với đường tròn vẽ từ B và C cắt nhau tại D .
a) Tính sđ góc BOC và sđ cung nhỏ AC .
b) chứng minh tứ giác OBDC nội tiếp .
c) Tia AC cắt tia BD tại E . Chứng minh D là trung điểm của BE .
d) Biết R=15cm . Tính diện tích hình quạt giới hạn bởi cung nhỏ AC( biết π=3,14)
Trên đường tròn tâm O đường kính AB=2R , lấy điểm C sao cho sđ cung BC=60° . Hai tiếp tuyến với đường tròn vẽ từ B và C cắt nhau tại D . a) Tính sđ góc BOC và sđ cung nhỏ AC . b) chứng minh tứ giác OBDC nội tiếp . c) Tia AC cắt tia BD tại E . Chứng minh D là trung điểm của BE . d) Biết R=15cm . Tính diện tích hình quạt giới hạn bởi cung nhỏ AC( biết π=3,14)
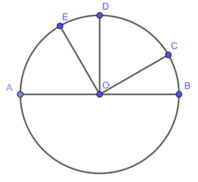
Cho đường tròn tâm O đường kính AB. Các điểm C, D, E cùng thuộc một cung AB sao cho sđ
∠
BC
1
6
sđ
∠
BA; sđ
∠
BD
1
2
sđ
∠
BA; sđ
∠
BE
2
3
sđ
∠
BA. So sánh hai cung nhỏ AE và BC.
Đọc tiếp
Cho đường tròn tâm O đường kính AB. Các điểm C, D, E cùng thuộc một cung AB sao cho sđ ∠ BC = 1 6 sđ ∠ BA; sđ ∠ BD = 1 2 sđ ∠ BA; sđ ∠ BE = 2 3 sđ ∠ BA. So sánh hai cung nhỏ AE và BC.
BT1: Trên đường tròn (O; R) lấy A,B,C sao cho dây AC=R, dây BC= R √ 2, tia CO nằm giữa tia CA và CB. Tính sđ các GÓC: AOC, COB, AOB. Tính sđ cung BC
BT2: Cho tam giác ABC cân tại A, góc A nhọn. Đường tròn (O), đường kính BC cắt AB, AC tại D và E.
CM: BE = CD ⇒ góc BDE = góc DEC.
CM: cung CE = cung BD