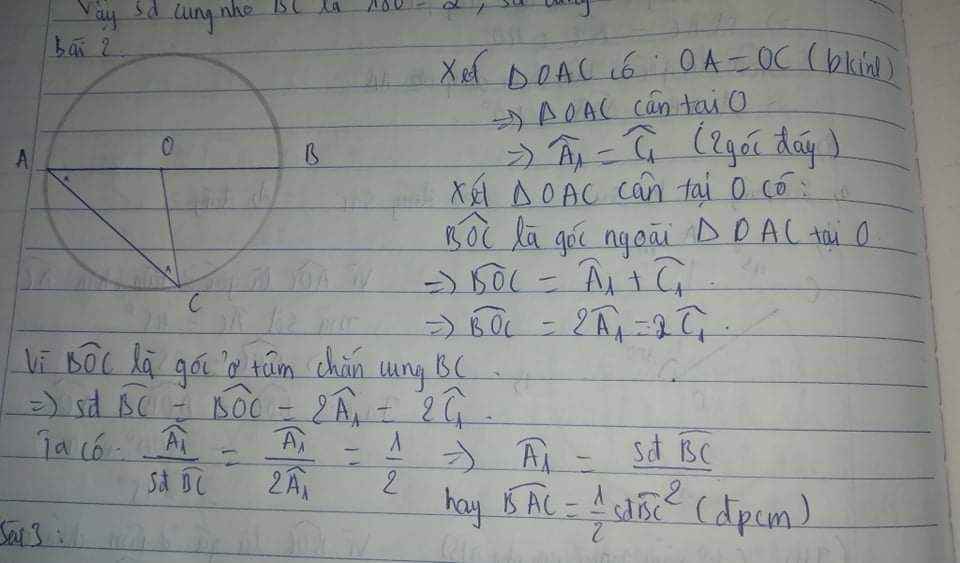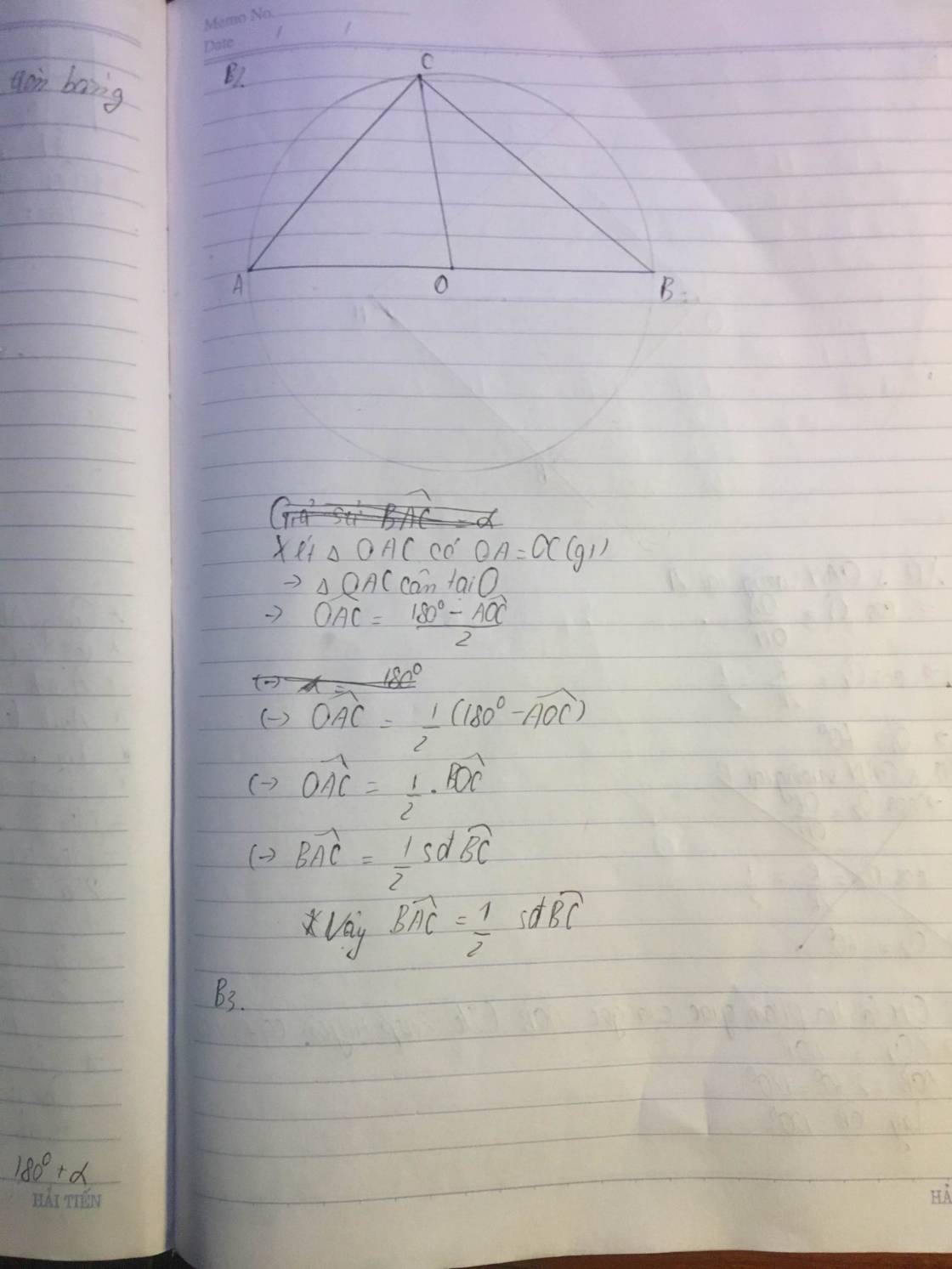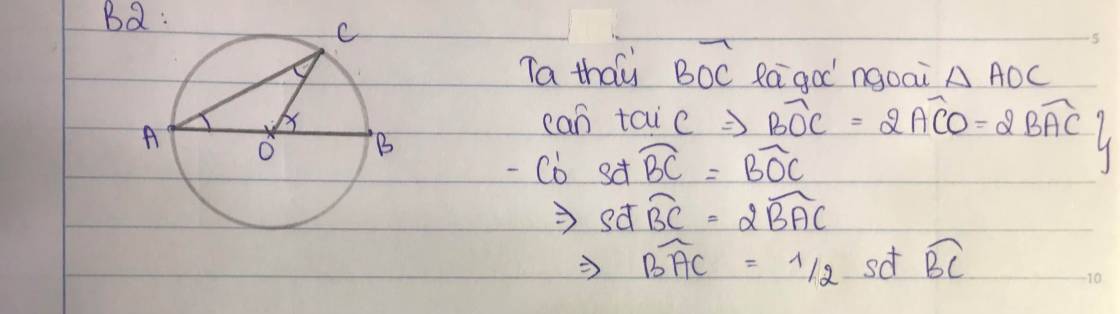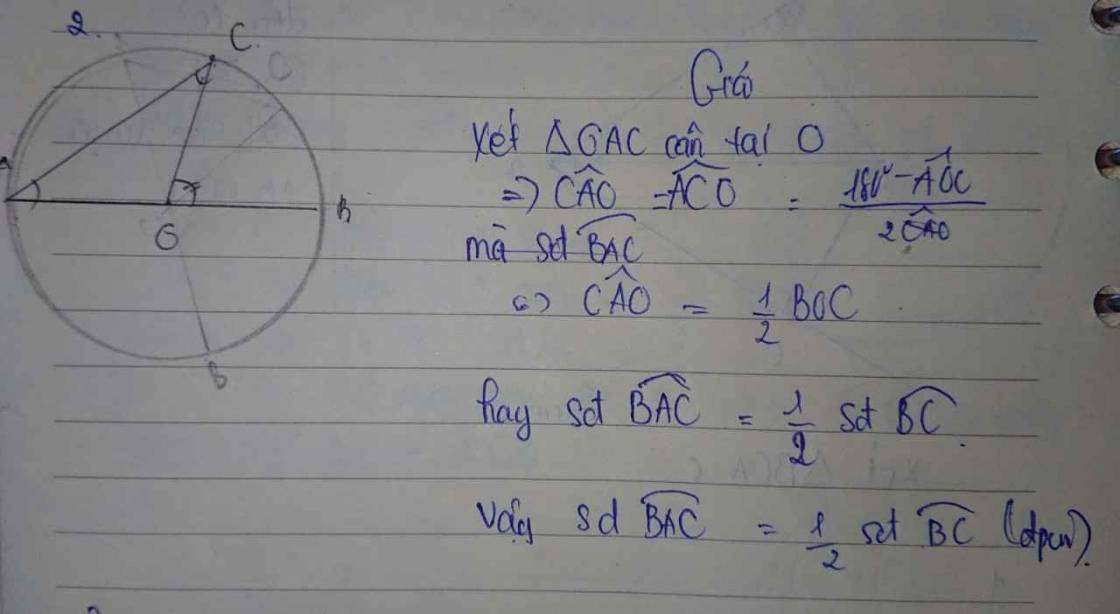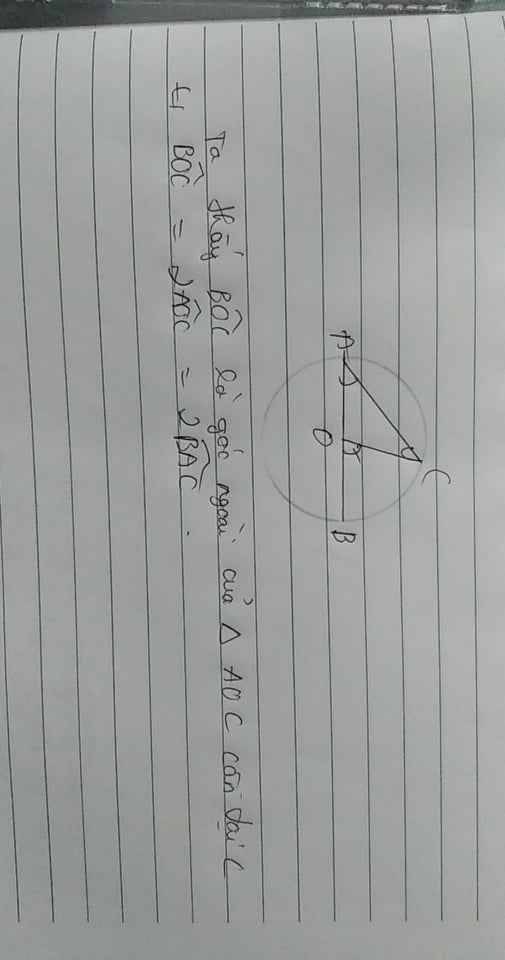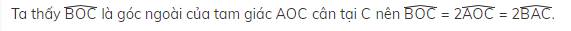Xét tam giascOAC cân tại O nên ta có góc \(\widehat{CAO}=\widehat{ACO}\)
mà ta có \(sd \widebat{BC}=\widehat{BOC}=\widehat{OCA}+\widehat{CAO}=2\widehat{CAO}=2\widehat{CAB}\)
vajay ta cos dpcm
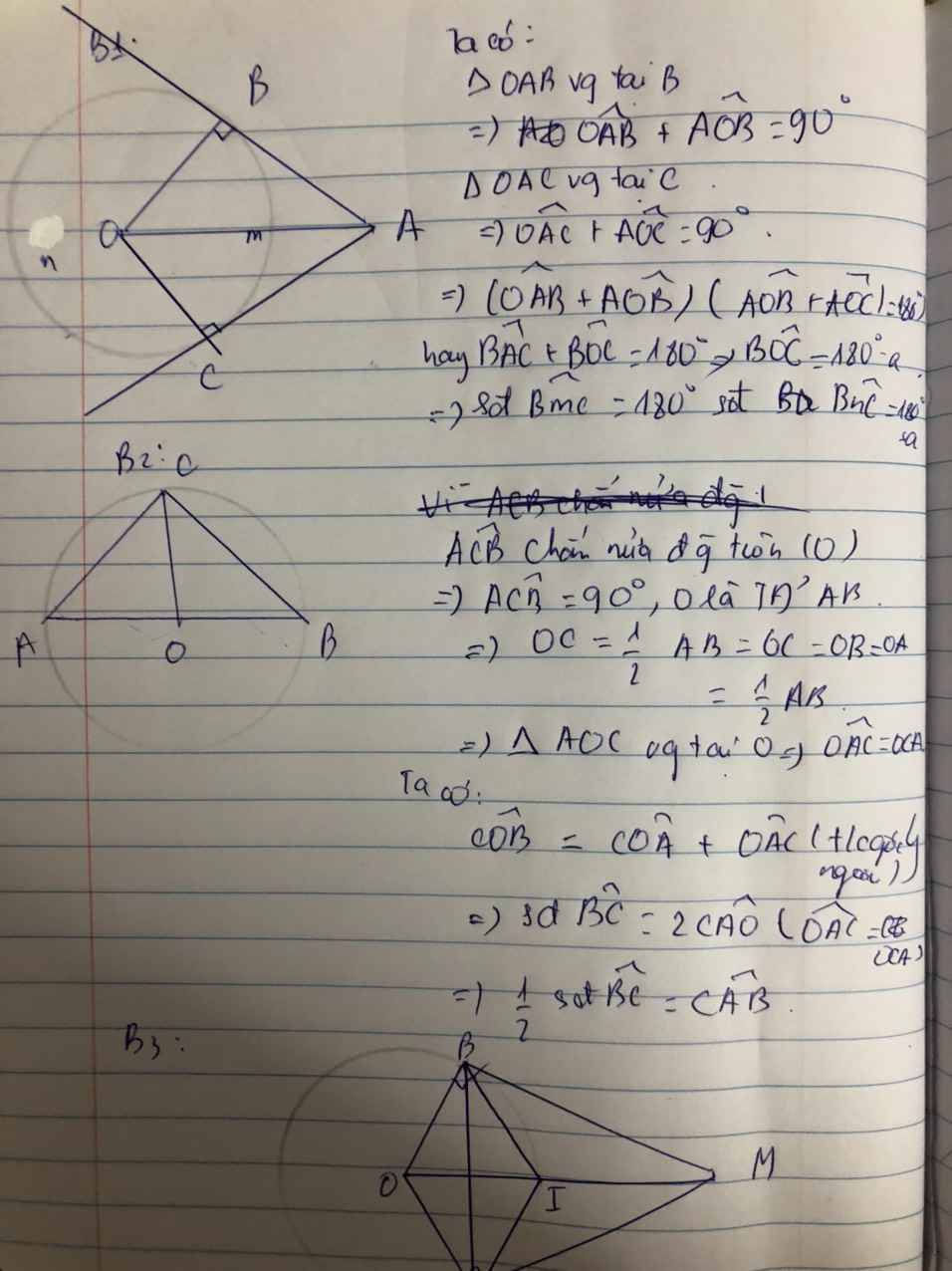
vì góc ACB chắn nửa đường tròn (O)
=> góc ACB = 90 độ mà O là trung điểm của AB
nên OC = 1/2 AB => OC=OB=OA=1/2AB
=> tam giác AOC cân tại O => góc OAC = góc OCA
Ta có góc COB = góc COA+góc OAC ( góc ngoài)
=> sđ cung BC = 2 góc CAO ( vì góc OAC=góc OCA)
=> 1/2 sđ cung BC = góc CAB
Vì gócACB chắn nửa đường tròn tâm O . Suy ra góc ACB = 90độ mà O là trung điểm của
áp dụng định lý về góc ngoài tam giác vào tam giác cân AOC ta có
góc BAC= 1 phần 2 góc BOC
SUY RA góc BAC =1/ 2 sđ CUNG BC
Ta thấy là góc ngoài của tam giác cân tại (1)
Xét △BOC có OC=OB=R => △BOC cân tại O (2)
Từ (1) và (2) => góc BOC = góc OBC = 60
Xét tam giác ABC nội tiếp đương tròn tâm O có AB là đường kính
=> tam giác ABC vuông tại C
=> góc BAC + góc ABC=90
=> góc BAC=90- góc ABC=90-60=30
Do đó BOC/BAC=60/30=2 hay BAC=1/2.BOC
xét (O) có :
OA=OC=R==>tam giác OAC cân tại O
Mà ^BOC là góc ngoài của tam giác OAC ==> ^BOC=2*^BAC
<==>^BAC=1/2cungBC
Xéttg OAC,ta có
OA=OC(=R)
Tg OAC cân tại O
Mà:BOC là góc ngoài tg OAC cân tại O
=>BOC=2.BAC
<=> BAC=1/2 BOC
Vậy .
Xét tam giác OAC có:OA=OC(=R)
Tam giác OAC cân tại O
Mà BOC là góc ngoài tám giác OAC
=>BOC=2.BAC
=> BAC=1/2.BOC
Vậy sđ BAC=1/2 sđ BC
Xét tam giác OAC có:OA=OC(=R)
Tam giác OAC cân tại O
Mà BOC là góc ngoài tám giác OAC
=>BOC=2.BAC
=> BAC=1/2.BOC
Vậy sđ BAC=1/2 sđ BC
Ta thấy ^BOC là góc ngoài của tam giác AOC cân tại C nên ^BOC=2^AOC=2^BAC.
vì góc ACB chắn nửa đường tròn (O)
=> góc ACB = 90 độ mà O là trung điểm của AB
nên OC = 1/2 AB => OC=OB=OA=1/2AB
=> tam giác AOC cân tại O => góc OAC = góc OCA
Ta có góc COB = góc COA+góc OAC ( góc ngoài)
=> sđ cung BC = 2 góc CAO ( vì góc OAC=góc OCA)
=> 1/2 sđ cung BC = góc CAB
Ta có góc BOC là góc ngoài của tam giác AOC cân tại đỉnh C
=> góc BOC= 2. góc OAC= 2. góc BAC
<=> góc BAC = \(\dfrac{1}{2}\) góc BOC = \(\dfrac{1}{2}\) góc BC
Ta thấy là góc ngoài của tam giác cân tại nên .
Ta thấy \widehat{BOC}