tìm hệ số góc của đường thẳng đi qua góc toạ độ và
a, đi qau điểm A (3;1)
b, đi qua điểm B (1;-3)
Những câu hỏi liên quan
tìm hệ số góc của đường thẳng đi qua góc toạ độ và
a, đi qau điểm A (3;1)
b, đi qua điểm B (1;-3)
a. Giả sử phương trình đường thẳng đi qua gốc tọa độ và đi qua A(3;1) là y=ax \(\Rightarrow1=3a\Rightarrow a=\dfrac{1}{3}\) ⇒ \(y=\dfrac{1}{3}x\) ⇒ hệ số góc của đường thẳng đó là \(\dfrac{1}{3}\)
b. Giả sử phương trình đường thẳng đi qua gốc tọa độ và đi qua B(1;-3) là y=a'x \(\Rightarrow-3=a\Rightarrow a=-3\) ⇒y=-3x ⇒ hệ số góc của đường thẳng đó là -3
Đúng 1
Bình luận (0)
Cho 2 điểm A(1; -2) và B(-4; 3)
a, Tìm hệ số góc của đường thẳng đi qua gốc tọa độ và qua điểm A .
b, Tìm hệ số góc của đường thẳng đi qua 2 điểm A và B .
a) Tìm hệ số góc của đường thẳng đi qua gốc tọa độ và đi qua điểm A(2; 1)
b) Tìm hệ số góc của đường thẳng đi qua gốc tọa độ và đi qua điểm B( 1; -2)
c) Vẽ đồ thị của các hàm số với hệ số góc tìm được ở các câu a), b) trên cùng một mặt phẳng tọa độ và chứng tỏ rằng hai đường thẳng đó vuông góc với nhau
trong mp toạ độ Oxy cho đường thẳng d có pt:y=(m-1)x+n. viết pt của d biết d đi qua điểm A(1;-1) và có hệ số góc bằng -3
Theo đề, ta có
m-1=-3 và (m-1)+n=-1
=>m=-2 và m+n=0
=>m=-2 và n=2
Đúng 0
Bình luận (0)
Tìm hệ số góc của đường thẳng đi qua gốc tọa độ và đi qua điểm:
a, Điểm A (3;1)
b, Điểm B (1;-3)
c, Vẽ các đường thẳng ứng với các hệ số góc vừa tìm được
d, Tìm chu vi và diện tích của tam giác AOB.
Trong không gian với hệ toạ độ Oxyz, cho hai điểm M(-2;-2;1), A(1;2;-3) và đường thẳng
d
:
x
+
1
2
y
-
5
2
z
-
1
. Tìm vectơ chỉ phương
u...
Đọc tiếp
Trong không gian với hệ toạ độ Oxyz, cho hai điểm M(-2;-2;1), A(1;2;-3) và đường thẳng d : x + 1 2 = y - 5 2 = z - 1 . Tìm vectơ chỉ phương u → của đường thẳng∆đi qua M, vuông góc với đường thẳng d đồng thời cách điểm A một khoảng bé nhất.
Đáp án B.
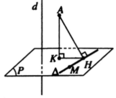
Gọi (P) là mặt phẳng qua M và vuông góc với d.Phương trình của 
Gọi H,K lần lượt là hình chiếu vuông góc cùa A trên ∆,(P)
Ta có: K(-3;-2;-1), 
Vậy khoảng cách từ A đến bé nhất khi A đi qua M,K.
∆ có vectơ chỉ phương 
Đúng 0
Bình luận (0)
Trong không gian với hệ toạ độ Oxyz, cho hai điểm M(-2;-2;1), A(1;2;-3)và đường thẳng
d
:
x
+
1
2
y
-
5
2
z
-
1
. Tìm vectơ chỉ phương
u
⇀
của đường thẳng
△
đi q...
Đọc tiếp
Trong không gian với hệ toạ độ Oxyz, cho hai điểm M(-2;-2;1), A(1;2;-3)và đường thẳng d : x + 1 2 = y - 5 2 = z - 1 . Tìm vectơ chỉ phương u ⇀ của đường thẳng △ đi qua M, vuông góc với đường thẳng d đồng thời cách điểm A một khoảng bé nhất
A. u ⇀ = (2; 1; 6)
B. u ⇀ = (1; 0; 2)
C. u ⇀ = (3; 4; -4)
D. u ⇀ = (2; 2; -1)
Tìm hệ số góc của đường thẳng đi qua gốc tọa độ và đi qua điểm A(2; 1)
Đường thẳng đi qua gốc tọa độ có dạng y = ax + b
Vì đường thẳng y = ax đi qua điểm A(2; 1) nên tọa độ điểm A nghiệm đúng phương trình đường thẳng.
Ta có: 1 = a.2 ⇔ a = 1/2
Vậy hệ số góc của đường thẳng đi qua gốc tọa độ và đi qua điểm A(2; 1) là a = 1/2
Đúng 0
Bình luận (0)
d) Tìm a, b để đồ thị hàm số đi qua điểm A(1; 2) và B(2;1)
e) Lập phương trình đường thẳng đi qua gốc toạ độ O và điểm A(1; 2)
f) Lập phương trình đường thẳng (d) đi qua M(2; -1) và vuông góc với đường thẳng (d’) có phương trình: y = −1 2 x +3