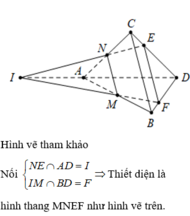
Những câu hỏi liên quan
cho tứ diện ABCD. Gọi M,N lần lượt là trung điểm cạnh AB, CD, E là điểm chia BC theo tỉ số BE/BC=1/2. Trên đoạn thẳng AM lấy điểm H. Tìm giao tuyến của mặt phẳng (P) đi qua H và song song với mặt phẳng (MNE). Tìm giáo tuyến của mặt phẳng (P) và mặt phẳng (BCD); mặt phẳng (P) và mặt phẳng (ABD)
Định chụp hình cơ cơ mà khá khó nhìn nên thoi đánh máy, bạn cố hiểu nhé
Từ H kẻ đường thẳng song song với ME cắt BC ở K
Từ K kẻ đường thẳng song song với EN cắt CD ở I
Nối I với H ta được mp (P) cần tìm
\(\left\{{}\begin{matrix}K\in HK\subset\left(HKI\right);K\in BC\subset\left(BCD\right)\\I\in KI\subset\left(HKI\right);I\in CD\subset\left(BCD\right)\end{matrix}\right.\Rightarrow\left(HKI\right)\cap\left(BCD\right)=KI\Rightarrow\left(P\right)\cap\left(BCD\right)=KI\)
Ta co \(\left\{{}\begin{matrix}H\in HK\subset\left(HKI\right);H\in AB\subset\left(ABD\right)\\KI//AB\end{matrix}\right.\)
=> Giao tuyen cua (P) va (ABD) la duong thang ua H va song song voi BD
Đúng 0
Bình luận (0)
Cho tứ diện ABCD. Gọi M,N lần lượt là trung điểm của AB, AC; điểm E trên cạnh CD sao cho
E
D
3
E
C
. Thiết diện tạo bởi mặt phẳng
M
N
E
và tứ diện ABCD là: A. Tam giác MNE B. Tứ giác MNEF với F là điểm bất kỳ trên cạnh BD C. Hình bình hành MNEF với F là điểm trên cạnh BD với EF//BC D. Hình thang MNEF với F là điểm trên cạnh BD sao cho EF//BC
Đọc tiếp
Cho tứ diện ABCD. Gọi M,N lần lượt là trung điểm của AB, AC; điểm E trên cạnh CD sao cho E D = 3 E C . Thiết diện tạo bởi mặt phẳng M N E và tứ diện ABCD là:
A. Tam giác MNE
B. Tứ giác MNEF với F là điểm bất kỳ trên cạnh BD
C. Hình bình hành MNEF với F là điểm trên cạnh BD với EF//BC
D. Hình thang MNEF với F là điểm trên cạnh BD sao cho EF//BC
Cho tứ diện ABCD. Trên cạnh AD lấy điểm M, trên cạnh BC lấy điểm N bất kì khác B,C. gọi (P) là mặt phẳng đi qua đường thẳng MN và song vs CD .khi đó thiết diện ABCD khi cắt bởi mặt phẳng (P) là hình gì ?
Cho tứ diện ABCD. Gọi M,N lần lượt là trung điểm các cạnh AB và AC. E là điểm trên cạnh CD với ED3EC. Thiết diện tạo bởi mp(MNE) và tứ diện ABCD là: A. Tam giác MNE B. Tứ giác MNEH với H là điểm bất kì trên cạnh BD C. Hình bình hành MNEH với H là điểm trên cạnh BD mà EH//BC D. Hình thang MNEH với H là điểm trên cạnh BD mà EH//BC
Đọc tiếp
Cho tứ diện ABCD. Gọi M,N lần lượt là trung điểm các cạnh AB và AC. E là điểm trên cạnh CD với ED=3EC. Thiết diện tạo bởi mp(MNE) và tứ diện ABCD là:
A. Tam giác MNE
B. Tứ giác MNEH với H là điểm bất kì trên cạnh BD
C. Hình bình hành MNEH với H là điểm trên cạnh BD mà EH//BC
D. Hình thang MNEH với H là điểm trên cạnh BD mà EH//BC
Đáp án C
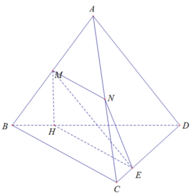
Xét (MNE) và (BCD) có:
E là điểm chung
BC // MN ⇒ BC // (MNE)
⇒ Giao tuyến của 2 mặt phẳng là đường thẳng d đi qua E và song song BC
d cắt BD tại H
⇒ MNEH là thiết diện cần tìm
Xét tứ giác MNEH có MN // EH ( // BC)
⇒ MNEH là hình thang
Đúng 0
Bình luận (0)
Cho tứ diện ABCD. Trên cạnh AD, BC theo thứ tự lấy các điểm M, N sao cho
M
A
A
D
N
C
C
B
1
3
. Gọi (P) là mặt phẳng chứa đường thẳng MN và song song với CD. Khi đó thiết diện của tứ diện ABCD cắt bởi mặt phẳng (P) là A. Một hình bình hành B. Một...
Đọc tiếp
Cho tứ diện ABCD. Trên cạnh AD, BC theo thứ tự lấy các điểm M, N sao cho M A A D = N C C B = 1 3 . Gọi (P) là mặt phẳng chứa đường thẳng MN và song song với CD. Khi đó thiết diện của tứ diện ABCD cắt bởi mặt phẳng (P) là
A. Một hình bình hành
B. Một hình thang với đáy lớn gấp 2 lần đáy nhỏ
C. Một hình thang với đáy lớn gấp 3 lần đáy nhỏ
D. Một tam giác
Cho tứ diện ABCD. Trên cạnh AD, BC theo thứ tự lấy các điểm M, N sao cho
M
A
A
D
N
C
C
B
1
3
. Gọi (P) là mặt phẳng chứa đường thẳng MN và song song với CD. Khi đó thiết di...
Đọc tiếp
Cho tứ diện ABCD. Trên cạnh AD, BC theo thứ tự lấy các điểm M, N sao cho M A A D = N C C B = 1 3 . Gọi (P) là mặt phẳng chứa đường thẳng MN và song song với CD. Khi đó thiết diện của tứ diện ABCD cắt bởi mặt phẳng (P) là
A. Một hình bình hành.
B. Một hình thang với đáy lớn gấp 2 lần đáy nhỏ.
C. Một hình thang với đáy lớn gấp 3 lần đáy nhỏ.
D. Một tam giác.
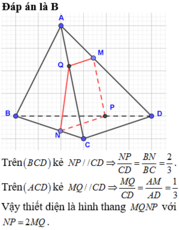
Đáp án là B

Trên (BCD) kẻ NP//CD

Trên (ACD) kẻ MQ//CD
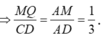
Vậy thiết diện là hình thang MQNP với NP=2MQ.
Đúng 0
Bình luận (0)
Cho tứ diện ABCD. Gọi M là trung điểm của AB. Cắt tứ diện ABCD bởi mặt phẳng đi qua M và song song với BC và AD, thiết diện thu được là hình gì?
A. Tam giác đều
B. Tam giác vuông
C. Hình bình hành
D. Ngũ giác
Cho tứ diện ABCD. Trên các cạnh AD, BC theo thứ tự lấy các điểm M, N sao cho
M
A
A
D
N
C
C
B
1
3
. Gọi (P) là mặt phẳng chứa đường thẳng MN và song song với CD. Khi đó thiết diện của tứ diện ABCD cắt bởi mặt phẳng (P) là A. một tam giác B. một...
Đọc tiếp
Cho tứ diện ABCD. Trên các cạnh AD, BC theo thứ tự lấy các điểm M, N sao cho M A A D = N C C B = 1 3 . Gọi (P) là mặt phẳng chứa đường thẳng MN và song song với CD. Khi đó thiết diện của tứ diện ABCD cắt bởi mặt phẳng (P) là
A. một tam giác
B. một hình bình hành
C. Một hình thang với đáy lớn gấp 2 lần đáy nhỏ
D. Một hình thang với đáy lớn gấp 3 lần đáy nhỏ
Cho tứ diện ABCD. Trên cạnh AB lấy một điểm M. Cho (α) là mặt phẳng qua M, song song với hai đường thẳng AC và BD.
a) Tìm giao tuyến của (α) với các mặt của tứ diện.
b) Thiết diện của tứ diện cắt bởi mặt phẳng (α) là hình gì?
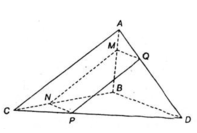
a) + (α) // AC
⇒ Giao tuyến của (α) và (ABC) là đường thẳng song song với AC.
Mà M ∈ (ABC) ∩ (α).
⇒ (ABC) ∩ (α) = MN là đường thẳng qua M, song song với AC (N ∈ BC).
+ Tương tự (α) ∩ (ABD) = MQ là đường thẳng qua M song song với BD (Q ∈ AD).
+ (α) ∩ (BCD) = NP là đường thẳng qua N song song với BD (P ∈ CD).
+ (α) ∩ (ACD) = QP.
b)Ta có:
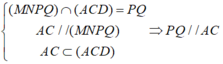
Suy ra, tứ giác MNPQ có các cạnh đối song song với nhau nên tứ giác MNPQ là hình bình hành.
Đúng 0
Bình luận (0)