5.

\(A=\dfrac{x}{x+\sqrt{x+yz}}+\dfrac{y}{y+\sqrt{y+zx}}+\dfrac{z}{z+\sqrt{z+xy}}\)

\(=\dfrac{x}{x+\sqrt{x\left(x+y+z\right)+yz}}+\dfrac{y}{y+\sqrt{y\left(x+y+z\right)+zx}}+\dfrac{z}{z+\sqrt{z\left(x+y+z\right)+xy}}\)

\(=\dfrac{x}{x+\sqrt{x^2+xy+yz+zx}}+\dfrac{y}{y+\sqrt{y^2+xy+yz+zx}}+\dfrac{z}{z+\sqrt{z^2+xy+yz+zx}}\)

\(=\dfrac{x\left(\sqrt{x^2+xy+yz+zx}-x\right)}{xy+yz+zx}+\dfrac{y\left(\sqrt{y^2+xy+yz+zx}-y\right)}{xy+yz+zx}+\dfrac{z\left(\sqrt{z^2+xy+yz+zx}-z\right)}{xy+yz+zx}\)

\(=\dfrac{x\sqrt{\left(x+y\right)\left(z+x\right)}-x^2}{xy+yz+zx}+\dfrac{y\sqrt{\left(x+y\right)\left(y+z\right)}-y^2}{xy+yz+zx}+\dfrac{z\sqrt{\left(z+x\right)\left(y+z\right)}-z^2}{xy+yz+zx}\)

Áp dụng BĐT \(ab\le\dfrac{a^2+b^2}{2}\) và BĐT \(a^2+b^2+c^2\ge ab+bc+ca\)

\(A=\dfrac{x\sqrt{\left(x+y\right)\left(z+x\right)}-x^2}{xy+yz+zx}+\dfrac{y\sqrt{\left(x+y\right)\left(y+z\right)}-y^2}{xy+yz+zx}+\dfrac{z\sqrt{\left(z+x\right)\left(y+z\right)}-z^2}{xy+yz+zx}\)

\(=\dfrac{x\sqrt{\left(x+y\right)\left(z+x\right)}+y\sqrt{\left(x+y\right)\left(y+z\right)}+z\sqrt{\left(z+x\right)\left(y+z\right)}-\left(x^2+y^2+z^2\right)}{xy+yz+zx}\)

\(\le\dfrac{x.\dfrac{2x+y+z}{2}+y.\dfrac{x+2y+z}{2}+z.\dfrac{x+y+2z}{2}-\left(x^2+y^2+z^2\right)}{xy+yz+zx}\)

\(=\dfrac{xy+yz+zx}{xy+yz+zx}=1\)

\(maxA=1\Leftrightarrow x=y=z=\dfrac{1}{3}\)

1.

a, \(A=(\dfrac{1}{2};2];B=[\dfrac{2}{3};+\infty)\)

b, \(A\cap B=\left[\dfrac{2}{3};2\right];A\cup B=\left(\dfrac{1}{2};+\infty\right)\)

2.

ĐK: \(x\ne2;x\ne-3\)

\(1+\dfrac{2}{x-2}=\dfrac{10}{x+3}-\dfrac{50}{\left(2-x\right)\left(x+3\right)}\)

\(\Leftrightarrow\dfrac{2}{2-x}+\dfrac{10}{x+3}-\dfrac{50}{\left(2-x\right)\left(x+3\right)}=1\)

\(\Leftrightarrow\dfrac{2\left(x+3\right)}{\left(2-x\right)\left(x+3\right)}+\dfrac{10\left(2-x\right)}{\left(2-x\right)\left(x+3\right)}-\dfrac{50}{\left(2-x\right)\left(x+3\right)}=1\)

\(\Leftrightarrow\dfrac{-8x-24}{-x^2-x+6}=1\)

\(\Leftrightarrow-8x-24=-x^2-x+6\)

\(\Leftrightarrow x^2-7x-30=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=10\left(tm\right)\\x=-3\left(l\right)\end{matrix}\right.\)

Bn để thẳng như z ko có đọc đc nha 

khó quá 

a) 11/12 x 9/19 - 22/24 x 6/19 + 11/12 x 16/19.

= 11/12 x 9/19 - 11/12 x 6/19 + 11/12 x 16/19.

=11/12 x (  9/19 -6/19 +  16/19)

=11/12x 1

=11/12

mình biết câu a/ thôi

nhìu số quá khó ko biết làm ;-;

\(\left(x-1\right)+\left(x-2\right)+....+\left(x-20\right)=610\)

\(x-1+x-2+...+x-20=610\)

\(\left(x+x+...+x\right)-\left(1+2+...+20\right)=610\)

Từ 1 đến 20 có 20 số hạng 

=> Tổng từ 1 đến 20 là: \(\left(20+1\right)\times20\div2=210\) 

=> \(x\times20+210=610\) 

                \(x\times20=610-210\) 

                \(x\times20=400\)

                         \(x=400\div20\) 

                         \(x=20\)

\(\left(x-1\right)+\left(x-2\right)+....+\left(x-20\right)=610\)

\(\left(x+x+...+x\right)-\left(1+2+3+...+20\right)=610\)

Ta thấy từ 1 đến 20 có 20 số hạng

=> Tổng từ 1 đến 20 là: \(\left(20+1\right)\times20\div2=210\) 

=> \(x\times20-210=610\) 

             \(x\times20=610+210\) 

             \(x\times20=820\) 

                     \(x=820\div20\) 

                     \(x=410\)

Em đã tìm được kết quả ạ.

(x - 1) + (x - 2) +.....+ (x - 19) + ( x - 20) = 610

=>(x + x + x...+ x) - (1 + 2 + 3 +...+ 20) = 610

=> 20x - 210 = 610.

=> 20x = 610+210

=> 20x = 820

=> x = 820 : 20

=> x = 41

Bạn Gia Khánh kết quả lần 2 của bạn gần đúng,bỏ số 0 thành 41 là được ạ.

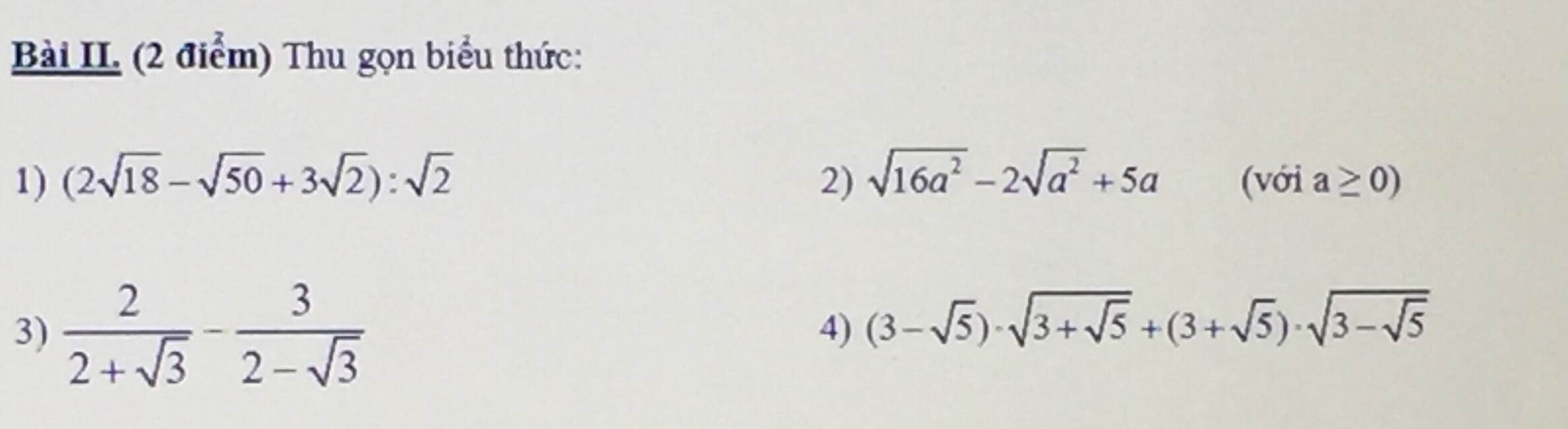
1)
\(=\left(6\sqrt{2}-5\sqrt{2}+3\sqrt{2}\right):\sqrt{2}=4\sqrt{2}:\sqrt{2}=4\)
2)
\(=16a-2a+5a=19a\)
3)
\(=\dfrac{2\left(2-\sqrt{3}\right)}{\left(2 +\sqrt{3}\right)\left(2-\sqrt{3}\right)}-\dfrac{3\left(2+\sqrt{3}\right)}{\left(2-\sqrt{3}\right)\left(\sqrt{3}+2\right)}\)
\(=4-2\sqrt{3}-6-3\sqrt{3}=-2-5\sqrt{3}\)

 

\(1,=\left(6\sqrt{2}-5\sqrt{2}+3\sqrt{2}\right):\sqrt{2}=4\sqrt{2}:\sqrt{2}=4\\ 2,=\left|4a\right|-2\left|a\right|+5a=4a-2a+5a=7a\left(a\ge0\right)\\ 3,=\dfrac{4-2\sqrt{3}-6-3\sqrt{3}}{\left(2+\sqrt{3}\right)\left(2-\sqrt{3}\right)}=\dfrac{-5\sqrt{3}-2}{4-3}=-5\sqrt{3}-2\\ 4,=\sqrt{\left(3-\sqrt{5}\right)^2\left(3+\sqrt{5}\right)}+\sqrt{\left(3+\sqrt{5}\right)^2\left(3-\sqrt{5}\right)}\\ =\sqrt{4\left(3-\sqrt{5}\right)}+\sqrt{4\left(3+\sqrt{5}\right)}\\ =2\sqrt{3-\sqrt{5}}+2\sqrt{3+\sqrt{5}}=2\left(\sqrt{3-\sqrt{5}}+\sqrt{3+\sqrt{5}}\right)\\ =2\left(\sqrt{\dfrac{6-2\sqrt{5}}{2}}+\sqrt{\dfrac{6+2\sqrt{5}}{2}}\right)\\ =2\left(\dfrac{\sqrt{5}-1}{\sqrt{2}}+\dfrac{\sqrt{5}+1}{\sqrt{2}}\right)\\ =2\cdot\dfrac{2\sqrt{5}}{\sqrt{2}}=2\sqrt{10}\)

Zế trái luôn ở tổng của các số giá trị tuyệt đối nên tổng ko âm

Nên phá đc dấu giá trị

=> x+19+x+5x+x+2020=5x

=>x+x+5x+x-5x=-19-2020

=>3x=-2039

=> x=-2039/3

TH1: x > 0 => l x + 19 l + l x + 5 l + l x + 2020 l = 5x                       TH2: x < 0 => l x + 19 l + l x + 5 l + l x + 2020 l = 5x

                        x + 19 + x + 5 + x + 2020 = 5x                                                        (-x) + 19 + (-x) + 5 + (-x) + 2020 = 5x

                       (x + x + x) + (19 + 5 + 2020) = 5x                                                     [(-x) + (-x) + (-x)] + (19 + 5 + 2020) = 5x

                       3x + 2044 = 5x                                                                                  3(-x) + 2044 = 5x

                       3x + 2044 = 3x + 2x                                                                          3(-x) + 2044 = 3(-x) + 2(-x)

                  => 2x = 2044                                                                                    => 2(-x) = 2044

                        x = 2044 : 2                                                                                         -x = 2044 : 2

                        x = 1022                                                                                              -x = 1022

                                                                                                                                     x = -1022

                                       Vậy x = 1022 hoặc x = -1022 (mình cũng ko chắc lắm đâu)

Bỏ TH2 đi.

 x = 1022 thôi

Khi tới VN thì lúc đó giờ bên Mỹ là:

(19+12) - 24= 7 (giờ) (1/1/2020)

Vậy giờ bên Mỹ sơm hơn giờ ở Việt Nam là: 13 - 7 = 6 (tiếng)

=> 1h30 30/1/2020 ở HN thì Paris lúc đó đang là 19h30 29/1/2020

(Tuy nhiên Mỹ thường không sớm hơn VN 6 tiếng mà sớm hơn nhiều tiếng luôn ớ)